СХЕМА
взаимосвязи
основных физических величин
по
разделу “Кинематика”
Приведенные в
предыдущем разделе понятия связаны
между собой различными
соотношениями, которые могут иметь
словесную формулировку или
выражаться в виде какой-либо
формулы. При решении задач важно
уметь отвечать на два разных
вопроса: что с чем связано и как
одно связано с другим. На второй
вопрос как раз и отвечают словесные
формулировки и формулы. Однако,
приступая к решению задачи более
важно уметь отвечать на первый
вопрос.
Для облегчения
поиска ответов на оба эти вопроса
мною придумана специальная схема.
По научному она называется “схема
операционно взаимосвязанных
категорий”. Суть ее проста: каждое
важное понятие из тех, которые были
названы в предыдущем разделе,
обозначается кружком с номером
внутри (например, кружок с номером 33
внутри него 33 обозначает понятие
“угловая скорость”).
На схеме разные
кружки соединяются линиями. Каждая
такая линия обозначает словесную
формулировку или формулу, в которую
входят ОБА понятия с внутренними
номерами (при этом в формуле или
формулировке могут встречаться и
другие понятия). Например, если
линия соединяет кружки с цифрами 33 и 30,
(33)--------(30)
то она изображает
формулу, связывающую радиус
окружности (номер 30) с угловой
скоростью (номер 33). Это линия
отвечает на вопрос что с чем
связано! На вопрос же "как
связано" отвечает сама формула
v = w · R,
в которой кроме
угловой скорости w и радиуса окружности R
присутствует еще и линейная
скорость v (знак · означает умножение).
Приведенная ниже
схема показывает, что с чем
связано в школьной кинематике.
Пояснения после схемы показывают, как
связаны соответствующие
физические понятия. Отметим, что
одна и та же формула связывает, как
правило, несколько понятий и может
изображаться несколькими линиями.
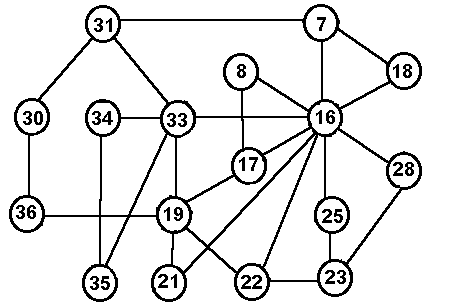
Вид у этой схемы
не очень красивый, но зато она
весьма полезна при решении задач по
кинематике. В ней обозначены не все
понятия, которые были приведены в
списке, а только самые необходимые.
Сейчас я приведу очень краткую (так
как все эти сведения можно найти в
любом школьном учебнике)
расшифровку каждого номера и
каждой линии на схеме.
- Объект (тело) -
любое тело в природе (машина,
космический корабль, камень и
т.д.).
- Материальная
точка - тело, размеры которого
не существенны в данной задаче.
Обычно это справедливо для
маленького тела, которое
находится рядом с большим
(камень падает на Землю, поезд
едет из одного города в другой
и т.п.).
- Механическое
движение - перемещение в
пространстве с течением
времени одного тела
относительно другого (или
частей тела). При механическом
движении меняется расстояние
между телами или между частями
тел.
- Поступательное
движение - движение, при
котором все точки тела
двигаются одинаковым образом,
т.е. траектории любых точек
тела можно наложить друг на
друга и они полностью совпадут.
При поступательном движении
тела можно следить лишь за
какой-то одной его точкой и
выбирать эту точку самым для
нас удобным образом.
- Вращательное
движение - движение, при
котором все точки тела лежат на
окружностях, центры которых
принадлежат одной прямой, а
плоскости взаимно параллельны.
- Траектория -
линия, по которой движется
материальная точка. Например,
реактивный самолет оставляет
за собой в небе белый след. Этот
след и есть траектория.
- Путь - длина
траектории. Чтобы найти путь
нужно вдоль траектории
проложить ниточку, потом
растянуть эту ниточку в прямую
линию и приложить к линейке.
- Перемещение -
вектор, соединяющий начальное
и конечное положение тела.
- Вектор -
направленный отрезок. По сути
дела это стрелка (стрела,
вылетевшая из лука и
сфотографированная в какой-то
момент).
- Координаты -
числовые характеристики,
однозначно задающие положение
точки в пространстве. В общем
случае необходимо знать три
числа, для того чтобы точно
указать положение одной точки.
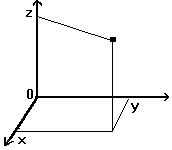
- Декартова
система координат -
специальная, удобная и самая
распространенная система
координат. Она представляет
собой три оси (т.е. попросту три
линейки), которые мы разместили
под углом 900 друг к другу.
Точка, из которой начинаются
оси, называется началом
координат. У наших линеек-осей
в этой точке расположено число
ноль. Если нужно обозначить
положение какого-то маленького
тела (материальной точки), то из
нее на каждую ось по
отдельности аккуратно
опускают перпендикуляр. Число,
которое отсекает это
перпендикуляр на оси и
называется координатой. Обычно
это координаты обозначаются
буквами x,y и z (см. Рисунок).
- Если тело
движется по прямой, то
достаточно одной оси для
описания его положения в любой
момент времени (например, оси
Х). В этом случае разность между
конечной и начальной
координатами равна
перемещению тела хк - хн = DS.
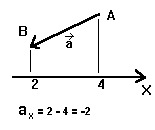
12. Проекция
вектора на ось - это отрезок
между точками на оси, который
получится, если из начала и
конца вектора опустить
перпендикуляры на ось.
Численное значение проекции
вектора на ось принимается
равным длине этого отрезка,
если направление проекции
совпадает с направлением оси, и
берется со знаком “минус”
если направление
противоположно.
На этом
рисунке приведен пример
нахождение проекции вектора 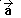 на ось
Х.
на ось
Х.
- Модуль вектора
- это просто его длина, т.е.
длина стрелки которой он
изображается. Если ах,
аy, аz это проекции
вектора, то его длина находится
с помощью теоремы Пифагора:
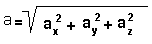
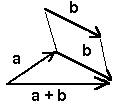
- Сумма векторов
- это такой вектор, который
рисуется по следующему
правилу. У нас есть два вектора,
т.е. две стрелки. Мы
параллельным переносом
сдвигаем один вектор (любой,
назовем его вторым) так, чтобы
его начало совпало с концом
другого (назовем его первым).
Потом мы рисуем стрелку,
которая выходит из начала
первого вектора в конец
второго. Эта стрелка и
называется суммой векторов.
- Начало отсчета
времени - это момент времени, в
который мы включили
секундомер. Конец отсчета
времени, соответственно момент
выключения секундомера.
- Интервал
(промежуток) времени движения -
промежуток времени от начала
движения на каком либо участке
пути до конца этого участка
(обозначается D t). Не нужно путать
интервал времени движения со
временем движения t, которое
показывает секундомер. Если
движение тела разбивается на
отдельные участки, то все время
движения складывается из
интервалов движения на каждом
отдельном участке.
- Средняя
скорость - это перемещение,
которое тело в среднем
совершает за единицу времени.
Формула для средней скорости
имеет вид:
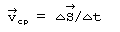 где D S - это перемещение
тела за промежуток времени D t.
Эта формула изображается на
схеме линиями 8 - 16, 8 - 17 и 16 - 17.
где D S - это перемещение
тела за промежуток времени D t.
Эта формула изображается на
схеме линиями 8 - 16, 8 - 17 и 16 - 17.- Средняя
путевая скорость - это путь,
который тело в среднем
совершает за единицу времени.
Формула для средней путевой
скорости имеет вид:
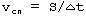 , где S -
это путь тела за промежуток
времени D t. Эта формула
изображается на схеме линиями 7
- 16, 7 - 18 и 16 - 18.
, где S -
это путь тела за промежуток
времени D t. Эта формула
изображается на схеме линиями 7
- 16, 7 - 18 и 16 - 18.
- Мгновенная
скорость - это средняя
скорость, взятая за очень
маленький промежуток времени
(такой маленький, что начальное
и конечное положение тела
отличить практически не
возможно). Эта скорость всегда
направлена по касательной к
траектории.
- Равномерное
движение - движение, при
котором тело за любые равные
промежутки времени совершает
равное перемещение. При
равномерном движении средняя
скорость совпадает с
мгновенной. Траекторией
является прямая линия вдоль
которой всегда можно направить
ось координат.
- Перемещение
при равномерном движении
совпадает с путем и связано со
скоростью и временем движения
формулой
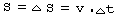 . Эта формула изображена
на рисунке линиями 16 - 21 и 19 - 21.
Координата тела при
равномерном движении
описывается законом x = xo
+ v· D t, где xo - начальная
координата тела (значение
координаты в начальный момент
времени), а v - скорость движения
тела. Эта формула не
изображается какой-либо
отдельной линией на схеме, но,
тем не менее, ее можно получить,
если использовать тот факт, что
величины 16 и 19 связаны друг с
другом (через величину 17).
. Эта формула изображена
на рисунке линиями 16 - 21 и 19 - 21.
Координата тела при
равномерном движении
описывается законом x = xo
+ v· D t, где xo - начальная
координата тела (значение
координаты в начальный момент
времени), а v - скорость движения
тела. Эта формула не
изображается какой-либо
отдельной линией на схеме, но,
тем не менее, ее можно получить,
если использовать тот факт, что
величины 16 и 19 связаны друг с
другом (через величину 17).
- Среднее
ускорение характеризует
быстроту изменения мгновенной
скорости тела. Среднее
ускорение по определению равно
отношению изменения скорости
тела к промежутку времени за
который это изменение
произошло, что выражается
формулой
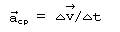
- Мгновенное
ускорение - это среднее
ускорение, взятое за очень
маленький промежуток времени
(точно также как мгновенная
скорость).
- Равноускоренное
движение - движение, при
котором скорость за любые
равные промежутки времени
изменяется одинаково. При
равноускоренном движении
мгновенное ускорение
совпадает со средним и, так как
их нет смысла отличать друг от
друга, то говорят просто слово
“ускорение”.
- Скорость и
ускорение при равноускоренном
движении связаны друг с другом
формулой
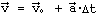 . Эта формула
изображается линиями 16 - 25 и 23 -
25.
. Эта формула
изображается линиями 16 - 25 и 23 -
25.
- Прямолинейное
движение - движение, при
котором траекторией является
прямая линия. При
прямолинейном движении
положение тела достаточно
задавать одной координатой
(например, х). Координата тела
связана с перемещением простой
формулой х = хо + D s (хо
- начальная координата, т.е.
координата в момент включения
секундомера).
- Прямолинейное
равноускоренное движение -
движения которое одновременно
является и прямолинейным и
равноускоренным. Такое
движение наблюдается, если
ускорение и начальная скорость
тела параллельны. Тогда тело
будет всегда находиться на
прямой, параллельной этим
векторам.
- Перемещение
при прямолинейном
равноускоренном движении.
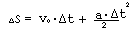 Данная формула
изображается линиями 16 - 28 и 23 -
28.
Данная формула
изображается линиями 16 - 28 и 23 -
28.- Движение по
окружности - движение, при
котором траекторией является
окружность.
- Радиус
окружности - отрезок,
соединяющий центр окружности с
точкой, лежащей на самой
окружности.
- Угловое
перемещение - угол между
радиусами, проведенными в
начальное и конечное положение
тела.
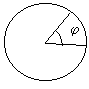
Угловое
перемещение обычно
обозначается буквой j
(фи).
- Равномерное
движение по окружности -
движение по окружности при
котором численное значение
скорости остается все время
постоянным.
- Угловая
скорость - физическая величина,
характеризующая быстроту
изменения углового
перемещения с течением
времени. При равномерном
движении по окружности угловая
скорость определяется
формулой w = j/D t, которая
изображается линиями 16 - 33 и 31 -
33. Угловая скорость также
связана со скоростью v формулой
V = wR, которая
изображена линией 19 - 33.
- Частота
вращения - количество оборотов
в единицу времени. Частота
связана с угловой скоростью
линией 33 - 34 и формулой w = 2pn.
- Период
вращения - время одного полного
оборота. Период связан с
частотой линией 34 - 35 (формула Т
= 1/n) и с угловой скоростью
линией 33 - 35 (формула T w = 2p).
- Центростремительное
ускорение - физическая
величина, характеризующая
быстроту изменения
направления скорости. При
равномерном движении по
окружности
центростремительное ускорение
направлено к центру окружности
и находится по формуле a = v2/R. Эта формула
изображается линиями 19 - 36 и 30 -
36.
Приведенный
список весьма краткий и далеко
неполный, но для решения
большинства типичных школьных
задач по кинематике его достаточно.
Отдельно напомним
закон сложения скоростей, который
сложно уложить в схему связи
понятий и категорий.
Закон сложения
скоростей звучит следующим
образом: при относительном
движении трех тел, вектора
скоростей этих тел связаны друг с
другом так, что вектор скорости
третьего тела относительно первого
(V31)
равен векторной сумме скоростей
третьего тела относительно второго
(V32)
и второго тела относительно
первого (V21). Итак, для ЛЮБЫХ трех
тел V31 = V32
+ V21 .
Зрительно запомнить эту формулу
очень легко - одна скорость
разбивается на две, причем между
цифрами 3 и 1 вставляется цифра 2.
Очень важно помнить, что это
формула имеет ВЕКТОРНЫЙ характер
(чтобы отличить вектор от числа мы
обозначаем его жирным шрифтом V , а число обозначаем
обычным шрифтом V).
Альманах
Предисловие
автора
Небольшое введение
для тех, кто только приступает к
изучению физики
Список
основных определений физических
понятий по разделу “Кинематика”
Задачи на понятия
“путь” и “перемещение”
Задачи на
прямолинейное равномерное
движение
Задачи на закон
сложения скоростей
Задачи на
прямолинейное равноускоренное
движение
Задачи на
прямолинейное равноускоренное
движение (продолжение 1)
Задачи на
прямолинейное равноускоренное
движение (продолжение 2)
Задачи на
прямолинейное равноускоренное
движение (окончание)
Задачи на
вертикальное падение
Задачи на
вертикальное падение (окончание)
P.S. Методика
организации уроков и примеры
используемых дидактических
материалов излагаются в файле Методика
и дидактика занятий по обучению
учащихся искусству решения задач
по физике



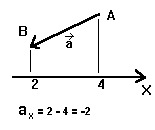
![]() на ось
Х.
на ось
Х.