Задача № 28.
Условие.
При свободном падении тело находилось в полете 8 с. С какой высоты оно упало и с какой скоростью врезалось в землю?
Решение.
Этой задачей открывается класс (т.е. множество, набор) задач на свободное падение. Основной ключевой признак - слово “падение” (слово “свободное часто не пишется, а только подразумевается). Что имеется в виду? А вот что. В таких задачах мы имеем дело с телом, которое падает вблизи поверхности земли. Это может быть выпущенный из руки камень, вылетевшие из ствола пуля или снаряд, выпущенная из лука стрела, прыгнувший с самолета парашютист и т.д.. Как правило, такое тело сначала сем-то разгоняется, чтобы приобрести начальную скорость (например, камень разгоняется рукой, пуля пороховыми газами и т.п.), но в момент отрыва от разгоняющего тела (камня от руки, стрелы от тетивы) тело начинает двигаться само по себе, по инерции. Поскольку все это происходит над землей, то она притягивает к себе летящее тело, и то рано или поздно падает на землю. Свободным называют падение, при котором тело не разгонялось, а было просто отпущено (например, мы разжали кулак, из которого выпал мячик и начал падать вниз). В этом случае тело падает без предварительного разгона, т.е. без начальной скорости.
Итак, признак “падение” означает, что мы имеем дело с падающим вблизи поверхности земли телом, а признак “свободно” говорит о том, что начальная скорость равна нулю.
Теперь самый важный вопрос, а что мы знаем про тела, которые падают вблизи поверхности земли? Есть ли что-то для всех них одинаковое, все их объединяющее? Да, есть. Впервые то, что объединяет все падающие тела, установил Галилей. В своих опытах он доказал, что ВСЕ ТЕЛА, ПРЕДОСТАВЛЕННЫЕ САМИМИ СЕБЕ, БЛИЗИ ПОВЕРХНОСТИ ЗЕМЛИ ПАДАЮТ С ОДНИМ И ТЕМ ЖЕ УСКОРЕНИЕМ, КОТОРОЕ НАПРАВЛЕНО ВЕРТИКАЛЬНО ВНИЗ (это правило справедливо, если не учитывать влияние воздуха). Это ускорение было названо ускорением свободного падения, оно было измерено и в системе СИ его значение равно примерно 9,8 м/с2. Для обозначения ускорения свободного падения обычно используется символ g. При решении задач часто можно округлять значение ускорения свободного падения до 10 м/с2.
Итак, если мы имеем задачу на ПАДЕНИЕ тел (и если в условии не сказано, что нужно учитывать трение о воздух), то для нас это означает, что мы имеем дело с телами, которые имеют ускорение g, направленное вертикально вниз и равное примерно 10 м/с2. Но если ускорение в процессе движения тела не меняется, значит, происходит равноускоренное движений! Значит, мы имеем дело с равноускоренным движением, ускорение которого равно g = 10 м/с2.
Пора, наконец, вернуться к нашей задаче.
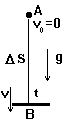
У нас имеется тело, которое свободно падает. Значит, оно не имеет начальной скорости (“свободно”) и движется равноускоренно с ускорением g= 10 м/с2, которое направлено вертикально вниз (“падение.”). Это самое главное, что мы должны определить из условия задачи, так как все остальное для нас уже не представляет труда. Сначала мы должны представить себе что происходит и начертить чертеж.
Это легко. Если камень поднять над землей и просто его отпустить, то он начнет падать вертикально вниз обратно к земле. Значит, траекторий движения тела в этом случае является прямая. Движение оказывается не только равноускоренным, но и прямолинейным. Двигаясь без начальной скорости (vo = 0) с ускорением g= 10 м/с2 по прямой АВ, тело за время t = 8 с совершило перемещение D S, приобретя конечную скорость v. Все признаки налицо, движение прямолинейное и равноускоренное, значит, для его писания нужно использовать общие формулы прямолинейного равноускоренного движения v = vo + at, D S = vo t + a t2/2.
В нашей конкретной задаче vo = 0, t = 8, а = g = 10, значит, получаем следующие конкретные равенства: v = 0 +10· 8 = 80 м/с, D S = 0· 8 + 10· 82/2 = 320 м.
Задача № 29.
Условие.
При свободном падении первое тело находилось в полете в 2 раза больше времени, чем второе. Сравнить их конечные скорости и перемещения.
Решение.
Ключевые слова нам уже известны - это “падение” и “свободном”. Опыт анализа предыдущей задачи нам подсказывает, что теперь просто два тела падают к земле. Каждое из них движется прямолинейно и равноускоренно с ускорением g (“падение”). Каждое из них не имело начальной скорости (“свободно”). Раз в задаче движется два тела, значит, мы должны использовать общие формулы равноускоренного движения тоже два раза. А чтобы мы не путали, какие формулы для какого тела, мы будем писать в них номера 1 и 2. Тогда:
для первого тела пишем v1 = gt1, D S1 = g t12/2;
для второго тела пишем v2 = gt2, D S2 = g t22/2.
Во всех формулах мы учли, что начальной скорости нет (vo = 0), и что ускорение движения тел равно ускорению свободного падения a = g.
По условию задачи мы должны сравнить, конечные скорости и перемещения тел. Сравнить - это означает найти отношение. Видно, что в токам отношении (дроби) будет присутствовать время движения. Что мы знаем про время движения? По условию первое тело находилось в два раза дольше второго. Это означает, что время движения первого тела t1 в два раза больше времени движения второго тела t2. Слова, как говориться, к делу не пришьешь, так что их нужно перевести в формула. Увеличить в 2 раза, это означает умножить на 2. Значит, в соответствии с условием t1 = 2· t2. Теперь легко найти требуемые отношения.
Сравниваем скорости:
v1/v2 = gt1/gt2 = t1/t2 = 2· t2/t2 = 2. Скорость первого тела в момент падения на землю будет в два раза больше скорости второго тела.
Сравниваем перемещения:
D S1/D S2 = (g t12/2)/(g t22/2) = t12/ t22 = (2· t2)2/ t22 = 4· t22/ t22 = 4. Перемещение первого тела в четыре раза больше перемещения второго тела.
Задача № 30.
Условие.
Снаряд зенитной пушки, выпущенный вертикально вверх со скоростью 800 м/с, достиг цели через 6 с. На какой высоте находилась цель? С какой скоростью снаряд вонзился в цель?
Решение.
Анализируем условие задачи, выделяем основные признаки, позволяющие нам определить характер движения тела и тем самым отнести рассматриваемую ситуацию к определенному классу задач.
Снаряд (тело) разгонялся в стволе пушки пороховыми газами, но при вылете из ствола остался предоставлен сам себе. Влияние воздуха мы не учитываем (раз не сказано учитывать его), значит, действует на снаряд во время полета только земля. Тело, брошенное вверх от земли, притягивается к ней обратно и через некоторое время начинает падать вниз. Если бы ни цель, в которую попал снаряд, он бы тоже упал на землю. Таким образом, хоть в условии задачи явно не было написано слово “падение”, но анализ происходящего в ней неизбежно привел к появлению данного ключевого признака.
Итак, мы опять имеем дело с падающим телом, траекторией которого является прямая (это написано в условии открытым текстом). Как мы уже знаем, рассматриваемая ситуация описывается моделью прямолинейного равноускоренного движения. Выписываем общие формулы прямолинейного равноускоренного движения:
v = vo + at, D S = vo t + a t2/2.
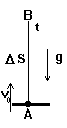
Для правильного использования данных общих формул в нашей конкретной ситуации необходимо нарисовать вспомогательной чертеж. Он очень похож на чертеж предыдущей задачи, только тело теперь движется вверх, значит и скорость его движения направлена вверх (по крайней мере, начальная скорость уж точно направлена вверх).
Снаряд движется из точки А в точку В, совершая за время t = 6 с перемещение D S. Начальная скорость снаряда vo = 800 м/с направлена вверх (к цели). Однако, ускорение свободного падения, с которым движется снаряд после вылета из ствола, по прежнему направлено вниз. Следует сказать, что в таких задачах часто ускорение снаряда направляют вверх. Что ж, в этом есть определенный смысл, ведь разгоняясь под действием пороховых газов, снаряд действительно двигался с ускорением вверх. Но это было ускорение снаряда В СТВОЛЕ орудия. Нас же интересуют события, которые происходят ПОСЛЕ вылета снаряда из орудия, когда он несется вверх уже ПО ИНЕРЦИИ, а его движение тормозится землей, которая притягивает его к себе обратно ВНИЗ! Поэтому в полете ускорение снаряда может быть направлено ТОЛЬКО К ЗЕМЛЕ.
Прежде чем подставлять в наши уравнения численные данный, следует сделать еще одно очень важное замечание. Мы с вами знаем, что скорость и ускорение являются величинами векторными. Для векторных величин при подстановке численных значений в уравнения нужно ОБЯЗАТЕЛЬНО учитывать их ЗНАК. Начальная скорость у нас направлена вверх и равно vo = 800 м/с = + 800 м/с. Написав у начальной скорости знак “+”, мы АВТОМАТИЧЕСКИ задали правило, по которому ВСЕ величины, направленные так же как начальная скорость имеют знак “+”. Но тогда все величины, направленные ПРОТИВ начальной скорости имеет знак МИНУС (“-”). В нашем случае ускорение свободного падения направлено против начальной скорости, значит, при подстановке в формулы оно должно браться со знаком “-”. Иначе говоря, ускорение движения нашего тела в данных условиях равно -10 м/с2; a = -g = -10. Теперь можно подставлять в формулы все известные нам численные данные. Подставляем, получаем:
v = 800 + (-10)· 6 = 740 м/с, D S = 800· 6 + (-10)· 62/2 = 4620 м.
Задача № 31.
Условие.
Одно тело свободно падает с высоты 10 м. Одновременно с ним начинает движения вертикально вниз второе тело с высоты 15 м. Какой должна быть начальная скорость второго тела, чтобы оба тела упали одновременно?
Решение.
В этой задаче основные признаки, это количество тел, начальные высоты, термины “свободное”, “ падает”, “вертикально вниз”, “начальная скорость”, “одновременно” (причем, два раза).
По всем этим признакам нам представляется следующая картина (на этом этапе наша работа схожа с работой врача, который по различным признакам ставит диагноз; горло красное - ангина, сильный насморк - ОРЗ). Первое тело с начальной скоростью v0 = 0 (“свободное”) в момент t0 = 0 начинает падать с высоты 15 м. Через время t оно упадет на землю, двигаясь с ускорением g. Движение, совершаемое телом - это прямолинейное равноускоренное движение (“падение”).
Второе тело начало свое движение в тот же момент, и упало, по условию задачи, тоже одновременно. Из этого следует, что оба тела находятся в полете одинаковое время. Значит, тело №2 начинает движение при t0 = 0, и заканчивает его в момент t. При этом оно падает с высоты 15 м, имеет начальную скорость V0 (которую надо найти) и движется прямолинейно (“вертикально вниз”) и равноускоренно с ускорением g (если тело бросить, то оно ПАДАЕТ).
Итак, беглый анализ ситуации показывает, что мы для обоих тел должны использовать формулы прямолинейного равноускоренного движения. Сначала вы должны записать эти формулы в общем виде, затем подставить в них конкретные значения, потом вычислить неизвестную величину. Сделайте это подробно, а я (поскольку мы уже многократно проделывали все эти действия) напишу сразу конкретные уравнения для перемещений тел:
первое тело; второе тело;
10 = 10· t2 /2, 15 = v0· t + 10· t2 /2.
При написании этих выражений я учел, что в нашей задаче сейчас все векторные величины (перемещения, скорости и ускорения тел) направлены в одну сторону (вниз к земле), следовательно, все они подставляются с одним знаком.
Решить полученную систему уравнений не представляет для нас труда. Мы сразу видим формулу с одной буквой, из которой находим время падения тел: t = Ц 2. Из второй формулы выражаем и вычисляем искомую начальную скорость второго тела: v0 = (15 - 5· 2)/Ц 2 = 3,54 м/с.
Задача № 32.
Условие.
Стрела, выпущенная из лука вертикально вверх, упала на землю через 6 с. Какова начальная скорость стрелы и максимальная высота подъем?
Решение.
Что есть в задаче? Тело - стрела. Каков характер движения тела? Что с ним происходит? Это нужно хорошо себе представить, а для этого нарисовать чертеж.
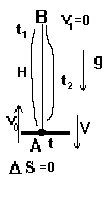
В начальный момент времени тело начинает двигаться из точки А вверх с начальной скоростью V0. Нужно помнить, что до этого момента стрела разгонялась тетивой. Не было бы тетивы, не было бы и начальной скорости у этой стрелы. Но в момент t0 = 0 стрела оторвалась от тетивы и начала подыматься вверх, двигаясь по инерции. Под действием притяжения земли, скорость стрелы будет уменьшаться и в точке В стрела на мгновение остановится, после чего начнет падать обратно на землю, двигаясь вниз. Раз о воздухе в условии задачи не говориться ни слова, значит его нет, нет и ветра, который мог бы сдувать стрелу вбок. Тогда в течение всего времени полета стрела будет находиться на прямой АВ, т.е. ее движение будет прямолинейным. Вылетев из точки А, стрела долетит до точки В и, через некоторое время, упадет обратно в точку А. В процессе своего движения она будет находиться только под влиянием земли, которая будет заставлять стрелу падать обратно. Раз мы имеем дело с падением, то, следовательно, мы имеем дело с равноускоренным движением. Итак, в нашей конкретной ситуации реализуется модель прямолинейного равноускоренного движения.
Какие физические величины существенны, важны для описания прямолинейного равноускоренного движения? Вспоминаем: это скорость (в том числе начальная), перемещение, ускорение и время движения. Все эти величины связаны друг с другом двумя формулами равноускоренного движения v = v0 + at; D s = v0 t + a t2/2.
Какие конкретные значения принимают эти физические величины в нашей конкретной задаче?
Тело переместилось за время t из точки А снова в точку А. Значит, оно в итоге не совершило никакого перемещения, т.е. D s = 0. Численное значение ускорения свободного падения равно 10 м/с2. Однако так как мы имеем дело с векторными характеристиками, нам нужно выбрать положительное направление, чтобы мы могли правильно расставить знаки. Раз тело выпустили вверх, то примем вверх и положительное направление. Тогда значение начальной скорости v0 будет положительным. А вот значение ускорения при таком выборе положительного направления будет отрицательным. (В математике положительное направление задают осью координат. Можно сказать, что мы направили ось координат вверх и проецируем на нее вектора скорости и ускорения). Значение конечной скорости тоже при таком выборе оси должно быть отрицательным, так как в момент падения скорость направлена вниз. Теперь мы можем подставлять в наши уравнения ускорение а = - 10 м/с2 и значение конечной скорости -v (величина v тогда будет положительная). Производим подстановку перемещения и ускорения: -v = v0 - 10· t; 0 = v0 t -10· t2/2. Что сейчас нужно делать? Правильно, искать формулу с одной буквой. Но такой формулы нет. Да и вообще, в этих двух формула у нас слишком много неизвестных. Такую систему уравнений мы решить не можем. Что же делать?
Если у нас в уравнениях слишком много неизвестных, значит, мы использовали слишком мало информации. Иначе говоря, есть что-то такое, что мы знаем, но до сих пор не сказали и не использовали. Что же это может быть такое? Снова возвращаемся к рисунку и тщательнее анализируем ситуацию.
В верхней точке тело остановилось, значит в точке В скорость v1 = 0. Это информация? Несомненно? Можем мы ее использовать? Пока не понятно. Но у нас нет другого выхода, как пытаться проговаривать и записывать в виде формул как можно больше наших знаний о происходящих в задаче событиях. Можно предположить, что формула v1 = 0 нам пригодится (все равно пока ничего другого у нас нет). Тогда нужно каким-то образом связать скорость v1 с остальными величинами задачи. Обозначим время движения из точки А в точку В t1. Высота H = АВ совпадает с перемещением D s1, которое тело совершает за время t1. Для участка движения АВ мы тоже можем записать формулы равноускоренного движения: v1 =0 = v0 - 10· t1; D s1 = H = v0 t1 -10· t1 2/2. Теперь у нас всего есть четыре формулы, но неизвестных величин в них пять: v, v0, t, t1, H. Значит, нам еще чего-то не хватает. Мы рассмотрели полное движение тела от точки А до точки А, Мы рассмотрели первую часть этого движения (от точки А до точки В). У нас осталась не рассмотренной только вторая часть - от точки В обратно до точки А. Придется взяться за нее. Обозначим время движения от точки В до точки А через t2. В точке В скорость стрелы была равна нулю. Перемещение от точки В до точки А равно H. Конечная скорость в точке А равна v. Мы можем уже записывать уравнения движения на участке ВА, но нужно аккуратно определиться со знаками векторных величин. Для этого надо посмотреть, направлены ли векторные величины на этом участке в одну сторону или в разные. При движении на участке ВА и ускорение, и скорость, и перемещение все направлены вниз, т.е. в одну сторону. Значит, у всех этих величин можно взять одинаковый знак “+”. Пишем уравнения движения на втором участке: v = 0 + 10· t2; H = 0· t2 + 10· t2 2/2. Теперь у нас уже целых шесть уравнений, и неизвестных стало побольше: появилось еще две неизвестных величины - v и t2. Всего у нас в деле появилось целое множество физических величин: начальная скорость, конечная скорость, высота, время движения вверх, время движения вниз, полное время движения. Причем, полное время движения складывается из времени движения вверх и вниз: t = t1 + t2. Похоже, мы провели такой подробный анализ ситуации, что вряд ли можно к нему что-нибудь добавить. Выпишем все полученные формулы вместе. Получим:
1) -v = v0 - 10· t; 2) 0 = v0 t -10· t2/2; 3) 0 = v0 - 10· t1; 4) H = v0 t1 -10· t1 2/2;
5) v = 10· t2; 6) H = 10· t2 2/2; 7) t = t1 + t2.
Теперь все зависит от того, как у нас с математикой.
В формулах № 4 и 6 слева стоит одна и та же высота Н. Следовательно, и правые стороны этих выражений равны друг другу. Тогда можем записать:
8) 10· t2 2/2= v0 t1 -10· t1 2/2.
Из формулы №3 выразим начальную скорость: v0 = 10· t1.
Подставляем это выражение вместо v0 в формулу №8 и получаем:
10· t2 2/2= 10· t1· t1 -10· t1 2/2, что дает 10· t2 2/2= 10· t12 -10· t1 2/2 = 10· t1 2/2.
Сокращаем на общие множители и получаем:
t2 2 = t1 2.
Так как время должно быть положительным, то после извлечения корня получаем, что время движения вверх равно времени движения вниз t2 = t1!
Давайте запомним этот факт! Если тело брошено с земли вверх, то оно в обе стороны движется за одинаковое время! Мы с вами только что математически доказали этот факт. Теперь мы сможем его использовать в любых других задачах (только нужно помнить, что в данной ситуации не учитывается влияние воздуха).
Из формулы №5 получаем сразу, что
9) v = 10· t2 = 10· t1 = v0.
Иначе говоря, тело падает обратно на землю с такой же по величине скоростью, с которой оно было брошено с нее. Это факт мы тоже запомним на будущее.
Теперь, наконец, найдем то, что от нас требуют: начальную скорость и высоту подъема.
По формуле №7, заменяя t2 на t1, получим t = t1 + t2 = t1 + t1 = 2· t1. Отсюда t1 = t/2. Но по условию задачи полное время падания равно 6 с, тогда время движения вверх (и вниз) равно t1 =t/2 = 6/2 = 3 с. Подставляя это значение в формулы № 6 и № 9, окончательно получаем: H = 10· t2 2/2 = 10· 3 2/2 = 45 м; v0 = v = 10· t1 = 10· 3 = 30 м/с.
Небольшое введение для тех, кто только приступает к изучению физики
Список основных определений физических понятий по разделу “Кинематика”
Схема взаимосвязи основных физических величин по разделу “Кинематика”
Задачи на понятия “путь” и “перемещение”
Задачи на прямолинейное равномерное движение
Задачи на закон сложения скоростей
Задачи на прямолинейное равноускоренное движение
Задачи на прямолинейное равноускоренное движение (продолжение 1)
Задачи на прямолинейное равноускоренное движение (продолжение 2)
Задачи на прямолинейное равноускоренное движение (окончание)