Задача №7.

Условие.

Скорость велосипедиста 36 км/ч, а скорость ветра 4 м/с. Какова скорость ветра относительно велосипедиста: а) при встречном ветре; б) при попутном ветре?

Решение.

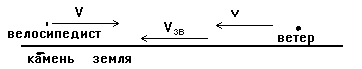
С чем мы имеем дело? С велосипедистом и ветром - это видно прямо из условия. Но есть и еще одно тело, о котором в условии не говориться, но без которого ничего происходить не может - это земля, по которой едет велосипедист и вдоль которой дует ветер. Два тела из трех движутся относительно третьего. Нам нужно ЗАПОМНИТЬ, что в ситуации, когда два каких-то тела движутся относительно третьего, необходимо использовать ЗАКОН СЛОЖЕНИЯ СКОРОСТЕЙ. Для того, чтобы его использовать, нужно его ЗНАТЬ, и нужно правильно НАРИСОВАТЬ ЧЕРТЕЖ. Начнем с чертежа. Сначала разберемся с вопросом под буквой а). Итак, по земле едет велосипедист, а ему навстречу дует ветер.

Стрелкой с заглавной буквой V обозначена скорость велосипедиста, а стрелкой с маленькой буквой v обозначена скорость ветра (они направлены навстречу друг другу).

Теперь надо перейти к закону сложения скоростей, но перед эти вспомним, что скорость - это величина относительная. Слово "относительная" означает, что скорость ВСЕГДА измеряется относительно чего-то. Наблюдатель смотрит на тело и измеряет скорость этого тела (пройденный телом путь делит на время, используя небольшие промежутки времени измерений). В результате получаем скорость ТЕЛА но относительно ЭТОГО наблюдателя. В нашей задаче на написано, относительно чего скорость велосипедиста равна 36 км/ч, а скорость ветра 4 м/с. Раз ничего специально не сказано, то это означает, что скорости измеряются с земли, т.е. это скорости тел относительно земли. Вот почему в такой ситуации нельзя забыть про землю. Что же такое скорость ветра относительно велосипедиста? Это такое значение скорости ветра, которое покажет прибор для измерения скорости ветра находящийся в руках велосипедиста. Из условия видно, что раз велосипедист и ветер сближаются, то расстояние между ними уменьшается быстрее, расстояние между ветром и камнем на земле. Значит скорость ветра относительно велосипедиста больше скорости ветра относительно камня (т.е. земли). Причем больше как раз на значение скорости самого велосипедиста. Таким образом, искомая скорость должна быть равна x = V + v. Для расчетов не забудем выразить скорости в одной и той же системе измерений, например, в системе СИ, для чего переведем 36 км/ч в метры в секунду:

36 км/ч = (36 · 1000 м)/(60мин· 60с) = 10 м/с. Тогда получаем, х = 10 + 4 = 14 м/с.

Мы получили этот ответ не используя закон сложения скоростей, а лишь исходя из наших простых соображений. Теперь посмотрим, как же такая задача решается в общем виде через закон сложения скоростей.

Закон сложения скоростей звучит следующим образом: при относительном движении трех тел вектора скоростей этих тел связаны друг с другом так, что вектор скорости третьего тела относительно первого (V₃₁) равен векторной сумме скоростей третьего тела относительно второго (V₃₂) и второго тела относительно первого (V₂₁). Итак, для ЛЮБЫХ трех тел V₃₁ = V₃₂ + V₂₁ . Зрительно запомнить эту формулу очень легко - одна скорость разбивается на две, причем между цифрами 3 и 1 вставляется цифра 2. Очень важно помнить, что это формула имеет ВЕКТОРНЫЙ характер (чтобы отличить вектор от числа мы обозначаем его жирным шрифтом V , а число обозначаем обычным шрифтом V). Складывать вектора - это складывать стрелки, которыми эти вектора изображаются. Но прежде чем эти стрелки складывать их нужно нарисовать. А для того, чтобы эти стрелки нарисовать, мы должны расставить номера у тел, с которыми в задаче имеем дело. Сделать это можно КАК НАМ ЗАБЛАГОРАССУДИТСЯ, но всегда найдется самый удобный способ. Нам нужно найти скорость ветра относительно велосипедиста (V₃₁), поэтому обозначим ветер номером 3, а велосипедиста номером 1. Для земли автоматически получаем номер 2. Теперь в законе скоростей вместо цифры 1 напишем "велосипедист", вместо цифры 2 напишем "земля", вместо цифры 3 напишем "ветер", и получим формулу вместо V₃₁ = V₃₂ + V₂₁ , которая будет иметь вид V_{ветер велосипедист} = V_{ветер земля} + V_{земля велосипедист} . Словами эту формулу можно прочитать так: скорость ветра относительно велосипедиста равна векторной сумме скоростей ветра относительно земли и земли относительно велосипедиста.

Скорость V_{ветер земля} у нас на рисунке уже есть - это просто скорость ветра (она и так дается относительно земли и направлена влево). Скорости V_{земля велосипедист} у нас на рисунке нет, зато есть скорость велосипедиста относительно земли, т.е. скорость V_{велосипедист земля}, которая направлена вправо.

Но если велосипедист едет мимо камня по земле вправо со скоростью 10 м/с, то камень удаляется от велосипедиста влево с той же скоростью 10 м/с! Значит, скорость земли относительно велосипедиста имеет то же численное значение, что и скорость велосипедиста относительно земли, только направлена в противоположную сторону.

Это мы можем записать в виде V_{земля велосипедист} = - V_{велосипедист земля}.

На рисунке скорость V_{земля велосипедист} изображается стрелкой, направленной против стрелки V, но такой же длины, и подписана V_зв. Чтобы найти скорость ветра относительно велосипедиста нам нужно сложить стрелки v и V_зв . Эти стрелки направлены в одну сторону и если их сложить, получим одну длинную стрелку с общей длиной, равной 14 м/с. Но эта длинная стрелка и есть скорость ветра относительно велосипедиста! Так что закон сложения скоростей дал нам ответ в случае а) 14 м/с (как мы и получили ранее).

Теперь рассмотрим быстро случай б). Он отличается от случая а) только тем, что ветер дует в ту же сторону, что и едет велосипедист. Для этого случая рисунок имеет следующий вид.

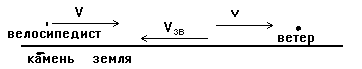
Закон сложения скоростей на зависит от того, куда дует ветер, значит он имеет тот же самый вид V_{ветер велосипедист} = V_{ветер земля} + V_{земля велосипедист} . Но теперь скорости v и V_зв направлены в ПРОТИВОПОЛОЖНЫЕ стороны! Значит мы должны складывать стрелки, направленные в противоположные стороны. Чтобы получить результат такого сложения, мы должны пройти из начальной точки вдоль одной стрелки (АВ), а затем идти в обратном направлении вдоль второй стрелки (ВС). Маленькая стрелка, идущая из начальной точки в конечную (АС) и есть результат такого сложения (смотрите на рисунок).

Видно, что длина маленькой стрелки равна разности длин исходных стрелок (хотя говорим мы про сумму векторов!). Итак, в случае б), чтобы найти чему равна скорость ветра относительно велосипедиста нужно вычесть из скорости велосипедиста (относительно земли) скорость ветра (относительно земли). В итоге находим, что x = V - v = 10 - 4 = 6 м/с.

Задача №8.

Условие.

Два поезда движутся навстречу друг другу со скоростями 72 и 54 км/с. Пассажир, находящийся в первом поезде, замечает, что второй поезд проходит мимо него в течение 14 с. Какова длина второго поезда?

Решение.

Наученные опытом решения предыдущей задачи, мы сразу отмечаем тела, которые движутся относительно друг друга: первый поезд с пассажиром, второй поезд и земля. Поезда движутся навстречу друг другу - это в точности совпадает со случаем а) задачи №5. Мы сразу можем сказать, что скорость второго поезда относительно первого равна 72 + 54 = 126 км/ч. Именно с такой скоростью пролетает второй поезд мимо пассажира, сидящего в первом поезде! Теперь мы имеем дело с другой ситуацией: тело (второй поезд) двигается с постоянной скоростью (126 км/ч) относительно другого тела (пассажир) в течение некоторого времени (14с). Основные характеристики тел этой ситуации - длина, скорость, время. Нам нужно еще рассматриваемую ситуацию обозначить (назвать, классифицировать). Так как (это видно из условия) скорость тела постоянна, то мы имеем дело с равномерным движением (пункт 20 в нашем списке основных величин). А при равномерном движении скорость (пункт 19), время (пункт 16) и расстояние (пункт 21) связаны друг с другом, причем связаны линиями 16-21 и 19-21, которые соответствуют формуле (смотрим список) S = Vt. В нашей задаче длина второго поезда - это и есть тот путь, который он проходит за 14 секунд, проезжая мимо пассажира первого поезда со скоростью 126 км/ч.

Осталось только сосчитать эту длину S = Vt = 126· (1000/3600)· 14=490 м.

Задача №9.

Условие.

Скорость движения лодки относительно воды в 2 раза больше скорости течения реки. Во сколько раз больше времени занимает поездка на лодке между двумя пунктами против течения, чем по течению?

Решение.

(С чем имеем дело?) В этой задаче у нас опять три тела: лодка, река и земля. (Что происходит?) Эти тела движутся относительно друг друга. (Каков характер движения?) По условию предполагается, что скорости тел постоянны (по крайне мере другого не говориться; говориться просто что скорость ЕСТЬ, т.е. подразумевается, что она во все моменты времени одинакова). Движение с постоянной скоростью называется равномерным. (Какие характеристики тел могут быть важны для движения данного вида?) При равномерном движении обычно являются существенны скорость, время и расстояние. (Какие закономерности могут быть существенны для данной ситуации?). При рассмотрении относительного движения может быть полезен закон сложения скоростей, а при рассмотрении равномерного движения может быть полезна связь между скоростью, временем и путем (которую мы видим, глядя на схему взаимосвязи понятий). Обратите внимание на осторожность формулировки, я не говорю "будет нужна", а говорю "может быть полезна". Это объясняется очень просто, ведь до тех пор, пока я задачу не решил, я не могу гарантировать, что мои предположения окажутся правильными. Только получив ответ, я смогу оглянуться назад и сделать вывод, что действительно оказалось нужным для решения данной задачи, а что мне не пригодилось.

Что нам теперь делать? Ответ должен быть уже очевиден - рисовать чертеж (точнее два, для движения по течению и для движения против). Сначала нарисуем случай "по".

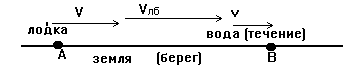
На этом рисунке большой буквой V обозначена скорость лодки относительно воды (течения) а маленькой буквой v обозначена скорость течения. Лодка из пункта А в пункт В движется относительно земли (берега). Скорость лодки относительно берега нам не известна. Нужна ли она нам? Да нужна. В формуле равномерного движения у нас РАССТОЯНИЕ ВДОЛЬ БЕРЕГА выражается через время движения и скорость ВДОЛЬ БЕРЕГА! Раз нам нужна скорость лодки относительно берега - найдем ее. Сделать это нам уже не представляет труда, так как у нас есть опыт применения закона сложения скоростей. Пусть лодка имеет №3, земля №1, а вода №2. Тогда можно сказать, что скорость лодки относительно берега равна векторной сумме скоростей лодки относительно воды и воды относительно берега:

V_{лодка берег} = V_{лодка вода} + V_{вода берег} = V + v.

Так как обе стрелки V и v направлены в одну сторону, то их суммарная стрелка будет направлена в ту же сторону и иметь суммарную длину. Тогда значение скорости лодки относительно берега (которая изображена на рисунке длинной стрелкой с обозначением V_лб) при движении по течению складывается из значений скорости лодки относительно воды и скорости воды относительно берега: V_лб = V + v. Если бы у нас были даны значения скоростей V и v, том бы сосчитали и значение V_лб. Но в данном случае придется ограничиться только формулой.

По условию задачи нам необходимо сравнить время движения лодки по и против течения. Так как движение равномерное, то есть формула, которая связывает скорость, путь и время. Формулу мы, конечно, не помним, но зато всегда можем подсмотреть ее в нашем списке. Нас интересует линя 16-21 или 19-21. Эта линия изображает формулу S = Vt. Для нас путь = АВ - расстояние от пункта А до пункта В, время = t_по - время движения по течению, а скорость = V_лб = V + v. Тогда можно подставить все эти выражения в общую исходную формулу и получить АВ = (V + v)t_по. Отсюда для времени движения по течению получаем t_по = АВ/(V + v).

Теперь рассмотрим движение против течения. Рисунок теперь немного изменится.

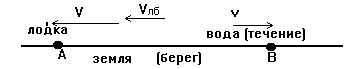
 Лодка теперь плывет из пункта В в пункт А. На закон сложения скоростей это не может оказать никакого влияния (те же самые тела продолжают двигаться относительно друг друга).

Так что и сейчас мы пишем V_{лодка берег} = V_{лодка вода} + V_{вода берег} = V + v. Но стрелки V и v сейчас направлены в противоположные стороны! Так что результатом их СЛОЖЕНИЯ будет маленькая стрелка V_лб, длина которой V_лб будет равна РАЗНОСТИ длин V и v: V_лб = V - v. Но поскольку и против течения движение носит характер равномерного, формула S = Vt применима и теперь. Путь = АВ, время = t_против - время движения против течения, скорость = V_лб = V - v. Можем записать, АВ = (V - v) t_против и найти отсюда время движения против течения t_против = = АВ/(V - v). Наша задача - найти во сколько раз время движения против течения больше времени движения по течению, т.е. вычислить дробь х = t_против/ t_по. Подставляя найденные выражения для времен, получим:

х = t_против/ t_по = [АВ/(V - v)]/ [АВ/(V + v)] = [АВ/(V - v)]· [(V + v)/АВ] =

= [АВ· (V + v)]/[ АВ· (V - v)] = (V + v)/ (V - v).

Что ж, кажется мы нашли ответ. На всякий случай посмотрим, все ли мы использовали из того, что есть в условии задачи? Еще раз внимательно читаем условие и видим, что мы использовали не всю информацию, заложенную в нем, а именно, мы не использовали до сих пор число 2. Конечно, есть задачи. в которых данных больше чем необходимо для решения, но прежде чем отбросить ту или иную информацию, нужно попробовать ее применить в решении, вдруг да это что-нибудь даст?! (Кстати, в подавляющем большинстве задач лишнего нет ничего). Итак, надо использовать число 2. Нам про него известно, что он показывает во сколько раз скорость лодки относительно воды (V) больше скорости воды относительно берега (v). Мы знаем по условию, что V в два раза больше v. Это хоть и правильные слова, но только слова, а задачи решаются вычислениями для которых необходимы формулы. Значит эти слова мы должны перевести в формулу. Сделать это просто (по крайней мере нам с вами, так мы знаем, что слов "больше в" означают действие "умножение"). По условию задачи записываем V = 2v. Это означает, что в конечной формуле этой задачи мы вместо величины V можем смело подставить величину 2v.

Тогда окончательно получаем: х = t_против/ t_по = (V + v)/ (V - v) = (2v + v)/ (2v - v) = 3.

Задача №10.

Условие.

Эскалатор метро поднимает неподвижно стоящего на нем пассажира в течение 1 мин. По неподвижному эскалатору пассажир поднимается за 3 мин. Сколько времени будет подниматься идущий вверх пассажир по движущемуся эскалатору?.

Решение.

В этой задаче мы имеем дело с тремя телами: человеком, эскалатором и землей - которые движутся относительно друг друга разнообразным способом. Это уже наводи нас на мысль о том, что для решения задачи может пригодиться закон сложения скоростей. Кроме того, наиболее важные параметры, которые характеризуют эти тела - это время движения (о чем говориться в условии открытым тестом), и кроме него возможно еще скорость (раз мы думаем про закон сложения скоростей) и расстояние (это подсказывает нам наш опыт решения подобных задач). Движение в рассматриваемых случаях подразумевается равномерным (с постоянной скоростью и вдоль одной прямой), что наводит на мысль о формуле равномерного движения.

У нас в задаче рассматриваются три различных ситуации: первая ситуация - движение эскалатора с неподвижным человеком; вторая ситуация - движение человека по неподвижному эскалатору; и третья ситуация - движение человека по движущемуся эскалатору. Во всех трех случаях можно говорить о времени движения, скорости движения и пройденном расстоянии. Стандартные обозначения для времени движения, скорости и расстояния - D t (время; в нашей ситуации рассматривается только один интервал движения, так что можно опустить знак D и считать t = D t), v (скорость), s (расстояние). Так как в разных ситуациях эти величины могут иметь разные значения, то мы будем снабжать их цифрами (индексами): t₁ , v₁ , s₁ - время, скорость и расстояние для первой ситуации; t₂ , v₂ , s₂ - время, скорость и расстояние для второй ситуации; t₃ , v₃ , s₃ - время, скорость и расстояние для третьей ситуации. Причем, дело осложняется еще и тем, что в каждом из трех рассматриваемых случаях мы имеем дело с тремя скоростями: у нас есть скорость человека относительно эскалатора, скорость эскалатора относительно земли и скорость человека относительно земли. Эти скорости тоже нужно отличать друг от друга, так что нам нужно ввести еще дополнительные различения. Скорость человека относительно земли обозначим v_чз1, v_чз2, v_чз3 (для каждого случая может быть своя скорость человека относительно земли. Конечно, он может быть и одинаковой, но до тех пор пока мы эти скорости НЕ ВЫЧИСЛИЛИ, пока мы только говорим о том что они ЕСТЬ И ВСЕ, мы обязаны считать их разными и отличать друг от друга). Подобным же образом обозначим скорость человека относительно эскалатора - v_чэ1, v_чэ2, v_чэ3 и скорость эскалатора относительно земли - v_эз1, v_эз2, v_эз3. (Внимательный читатель спросит, а почему именно эти три вида скорости были мною выбраны? Отвечу просто, потому что в свое время я перепробовал все иные возможные варианты, которые существуют для трех движущихся тел, и пришел к выводу, что этот самый удобный. Фактически я проделал нумерацию тел, обозначил землю номером 1, эскалатор номером 2 и человека номером 3, предполагая что мне пригодится закон сложения скоростей, который и использует нумерацию).

Давайте, наконец, нарисуем чертеж.

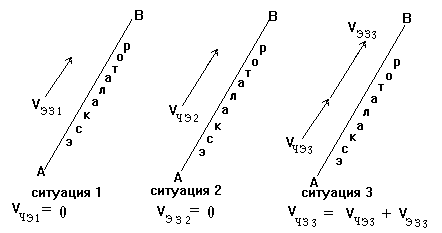
Теперь пора приступить к расчетам.

Во всех трех случаях происходит равномерное движение (признак - постоянная скорость). Значит во всех трех случаях можно использовать формулу s = vt, только написать ее нужно три раза: s₁ = v₁ t₁ , s₂ = v₂ t₂ , s₃ = v₃ t₃ . Во всех трех случаях путь - это путь пройденный человеком относительно земли, время - это время этого движения, значит скорость - это скорость ЭТОГО движения, т.е. скорость человека относительно земли. Значит наши формулы можно переписать в виде s₁ = v_чз1 t₁ , s₂ = v_чз2 t₂ , s₃ = v_чз3 t₃ . Путь, пройденный человеком от точка А до верхней точки В во всех трех случаях одинаковый и равный АВ (s₁ = s₂ = s₃ = АВ), значит наши формулы можно переписать в виде

АВ = v_чз1 t₁ , АВ = v_чз2 t₂ , АВ = v_чз3 t₃ .

Нам нужно найти время движения от нижней точки до верхней в третьем случае, т.е. найти t₃. Я пока не знаю КАК вычислить искомое время, но я знаю КАК подойти к этому вычислению. Все что у меня есть - это закон равномерного движения и закон сложения скоростей. Значит я должен выжать из этих законов ВСЕ ЧТО ТОЛЬКО МОЖНО, глядишь, и решение найдется. Практически каждая задача решается подобным образом. Главное - делать все аккуратно и внимательно, обозначать разными буквами все разные величины чтобы их не спутать и внимательно перечитывать условие, чтобы не пропустить какую-нибудь важную информацию.

Что еще мы можем использовать?

В первом случае человек стоит на эскалаторе неподвижно, значит его скорость относительно эскалатора равна нулю, т.е. v_чэ1 = 0. Во втором случае эскалатор неподвижен, т.е. скорость эскалатора относительно земли рана нулю v_эз2 = 0. По закону сложения скоростей во всех трех случаях скорость человека относительно земли равна векторной сумме скоростей человека относительно эскалатора и эскалатора относительно земли (легко запомнить: нас интересует отношение человека и земли, а эскалатор является промежуточным телом). Формула для закона сложения скоростей во всех случаях выглядит так: v_чз1 = v_чэ1 + v_эз1 или v_чз2 = v_чэ2 + v_эз2 или v_чз3 = v_чэ3 + v_эз3. Вместо v_чэ1 пишем ноль, вместо v_эз2 тоже пишем ноль и получаем из первых двух формул v_чз1 = v_эз1 и v_чз2 = v_чэ2. Мы использовали и закон сложения скоростей, и закон равномерного движения, но как найти нужное время пока так и не знаем. Это означает, что мы знаем еще что-то важно для решения задачи, но до сих пор нами не использованное. Вернемся опять к тому что происходит. Представим себе эту ситуацию. Понятно, что эскалатор и с покоящимся человеком, и с бегущим человеком, и без человека движется всегда с одной и той же скоростью (если он конечно движется). Значит скорость движения эскалатора относительно земли одна и та же и в случае 1, и в случае 3. Пишем v_эз1 = = v_эз3. Значит будет выполняться и другое равенство v_чз1 = v_эз1= v_эз3, или просто v_чз1 = v_эз3. Дает ли нам что-нибудь эта новая формула? Конечно! Ведь до сих пор у нас не было ни одной формулы с разными цифрами у скоростей. На по условию известны времена движения в первом и второй ситуациях, а найти нужно для третьей. Значит это искомое время должно выражаться через те времена, которые даны. Значит мы должны величины с номерами 3 каким-то способом выразить через величины с номерами 1 и 2. Формула v_чз1 = v_эз3 нам это как раз и дает! Кроме того, теперь мы можем избавиться от скорости эскалатора v_эз3, заменив ее скоростью человека v_чз1. Тогда мы получим v_чз3 = v_чэ3 + v_чз1. В этой формуле уже все скорости - это скорости человека, но две из них относительно земли (что хорошо, так как они же есть и в формулах с расстоянием АВ), а скорость v_чэ3 - относительно эскалатора. Хорошо бы избавиться и от нее, было бы проще жить. Сделать это просто. Когда человек бежит по эскалатору, ему не важно, движется ли тот или нет. Значит и в третьем случае и во втором скорость движения человека относительно эскалатора одна и та же: v_чэ3 = v_чэ2. Но мы уже знаем, что v_чз2 = v_чэ2. Тогда имеем v_чэ3 = v_чз2. Это дает нам формулу v_чз3 = v_чз2 + v_чз1. На рисунке видно, что все скорости направлены в одну и ту же сторону, значит их численные значения просто складываются, т.е. v_чз3 = v_чз2 + v_чз1. Вот теперь наступила пора законов равномерного движения. Из них мы дли каждого случая получаем

v_чз3 = АВ/t₃ , v_чз2 = АВ/t₂ , v_чз1 = АВ/t₁ .

Подставляя вместо значений скоростей их выражения, имеем следующее

АВ/t₃ = АВ/t₂ + АВ/t₁ .

Сокращаем слева и справа на общий множитель АВ, получим:

1/t₃ = 1/t₂ + 1/t₁ = 1/3 + 1/1 = 4/3, откуда t₃ = 3/4. Так как значения времени я подставлял в минутах, то и ответ получил в минутах, t₃ = 3/4 мин = 45 с.

Задача №11.

Условие.

Вертолет летел на север со скоростью 20 м/с. С какой скоростью и под каким углом к меридиану будет лететь вертолет, если подует западный ветер со скоростью 10 м/с?

Решение.

Рисуем рисунок и одновременно анализируем ситуацию: тут север (С), тут запад (З); Это вертолет (В) без ветра (его скорость V направлена вдоль земли на север), а это он (В) с ветром (когда подул ветер, то вертолет стало сносить в сторону; западный ветер дует с запада на восток со скоростью v, вертолет же теперь начинает лететь в бок со скоростью V₁). У нас опять налицо движение трех тел: вертолета, ветра и земли - так что опять нужен будет закон сложения скоростей.

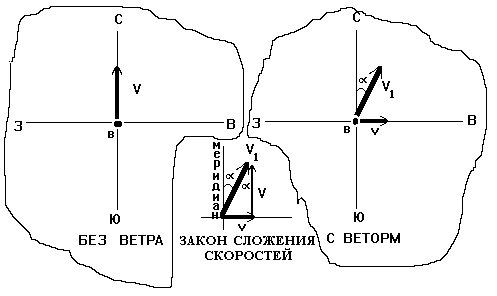
Когда западный ветер начал сносить вертолет к востоку, то курс вертолета стал отклоняться от меридиана и составил угол a к нему. (Заметьте, как много нам нужно было знать только для того, чтобы понять, о чем в задаче идет речь: как расположены стороны света, как дует западный ветер, что такое меридиан - без этих предварительных знаний нам задачу точно не решить.)

В задаче нет ни слов ни о времени движения, ни о пройденном пути или перемещение - только скорости относительного движения. Все что мы можем попробовать использовать для описания относительного движения - это закон сложения скоростей. Причем, когда ветра не было, в движении находилось только одно тело - вертолет. Он летел относительно земли. Но хоть ветра то и не было, но воздух то был, просто он был неподвижен! Значит, скорость вертолета относительно земли совпадала в первом случае со скоростью вертолета относительно воздуха. Таким образом, делаем вывод, что скорость вертолета относительно воздуха равна V = 20 м/с. Когда подул ветер, это означает, что воздух стал перемещаться относительно земли, и этот самый воздух стал увлекать за собой вертолет. Теперь-то и пришла пора применить закон сложения скоростей. Скорость вертолета относительно земли теперь складывается из скорости вертолета относительно воздуха и скорости воздуха относительно земли (как вы думаете, как я перенумеровал тела, чтобы сформулировать закон сложения скоростей именно таким образом? Правильно, земля - №1, воздух (промежуточное тело) - №2, вертолет - №3). Используя обозначения, можно сказать, что скорость V₁ = V + v, только нужно помнить, что мы складывать должны вектора, т.е. стрелки! Как складывать стрелки показано на рисунке: нужно к концу стрелки v приставить начало стрелки V, а затем соединить начало стрелки v с концом стрелки V. В результате получим стрелку V_1. Нам нужно найти скорость вертолета относительно земли во втором случае, т.е. длину стрелки V₁. Известны же нам длины стрелок v и V; V = 20 м/c, v = 10 м/c. Если бы стрелки v и V были направлены по одной прямой, то мы бы знали что делать - просто бы их сложили или вычли, как это мы делали в предыдущих задачах. Сейчас тоже что-нибудь придумаем.

Кроме чертежа у нас нет ничего, так что все равно пользоваться больше нечем. Значит, внимательно рассматриваем чертеж. Чертеж - это из области геометрии. Что-нибудь геометрическое, какую-нибудь геометрическую фигуру может быть узнаем? Конечно! Мы видим треугольник! (В физике его называют треугольником скоростей). Все три стрелки образуют треугольник. Стрелка V направлена на север, а стрелка v на восток (с запада). Между направлениями на восток и север угол 90^о, т.е. прямой угол. Значит между стрелками v и V тоже прямой угол. А это означает, что треугольник скоростей ПРЯМОУГОЛЬНЫЙ! Вот теперь совсем другое дело. Про прямоугольный треугольник мы знаем массу всякой полезной информации, например теорему Пифагора. Нам нужно найти длину V₁, т.е. длину гипотенузы в нашем прямоугольном треугольник. По теореме Пифагора сразу можем записать (V₁)² = V² + v² = 20² + 10² = 500. Тогда сама V₁ = Ц 500 = 22,36 м/с. Осталось найти угол к меридиану. Он у нас обозначен буквой a . Такой же угол есть и в нашем прямоугольном треугольнике (по теореме о прямой, которая пересекает две взаимно параллельные прямые). Про прямоугольный треугольник мы знаем, что углы в нем выражаются через различные тригонометрические функции, например через синус или тангенс. Нам без разницы, что использовать для нахождения угла, возьмем тангенс (он часто встречается в подобных задачах). Тангенс угла равен отношению катетов, причем в числителе должна стоять величина катета, противолежащего данному углу. Тогда мы можем записать tg a = v/V = 10/20 = 0,5. Тангенс какого угла равен 0,5 (ищем в таблицах)? Правильно, примерно двадцати семи градусов. Значит угол a = 27^о (a лежит в пределах от 0^о до 90^о и по правилам математики a =arctg(0,5) ). Конец задачи.

Задача №12.

Условие.

Катер, переправляясь через реку, движется перпендикулярно течению реки со скоростью 4 м/с относительно воды. На сколько метров будет снесен катер течением, если ширина реки 800 м, а скорость течения 1 м/с?

Решение.

Задача очень похожа на предыдущую. С чем имеем дело? Опять с тремя телами - катер, вода, земля. Катер плывет поперек течения, а вода его сносит (в точности так же как ветер сносит вертолет в предыдущей задаче). Можно сразу нарисовать чертеж и применить закон сложения скоростей (мы еще не знаем, зачем он нам сейчас, этот закон, но опыт показывает, что без него скорее всего не обойтись, так что мы сначала выжмем из него все что только сможем, а уж потом будем думать как это использовать). Рисуем.

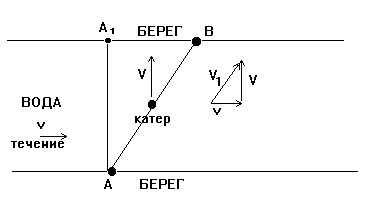
Если бы вода не текла (озеро), то катер двигался бы от берега к берегу по стрелке V и из точки А попал бы точно в точку А₁. Но вода течет вдоль берега со скоростью v и сносит катер за собой вправо, так что на самом деле он попадает в точку В. Вектор V - это скорость катера относительно воды, вектор v - это скорость воды относительно берега. Человек же, стоящий на берегу (в точке В например), наблюдает скорость катера относительно земли. Про нее мы пока знаем только лишь то, что она есть (обозначим ее V₁) и что она отличается от v и от V. По закону сложения скоростей, скорость катера относительно земли (V₁) равна векторной сумме скоростей катера относительно воды (V) и скорости воды относительно берега (т.е. скорости течения v); V₁ = V + v. Как складывать вектора мы уже знаем и смело рисуем треугольник скоростей. Именно вдоль скорости V₁ движется катер из точки А в точку В. Это означает, что отрезок АВ и вектор V₁ параллельны друг другу. Если бы течения не было, то катер двигался бы со скоростью V из точки А в точку А₁, т.е. отрезок АА₁ и вектор V параллельны друг другу. Река же течет вдоль берега, значит параллельно ему. Тогда отрезок А₁В параллелен скорости v. В итоге мы получаем, что треугольник АВА₁ и треугольник скоростей имеют взаимно параллельные стороны, а из геометрии мы знаем, что треугольники со взаимно параллельными сторонами подобны. Сами того не замечая, мы получили очень важную информацию. Все что мы делали - это аккуратно рисовали на чертеж и анализировали все, что при этом получается. А получили, что треугольники подобны. Это означает, что мы можем использовать свойства подобных треугольников. Например, мы можем записать равенства для отношений сторон. Зачем нам это нужно мы не знаем, но при решении задач очень помогает следующее правило: "Если что-то можно сделать, значит это нужно сделать!". Пишем:

АА₁/ВА₁ = V/v, АА₁/АВ = V/V₁, ВА₁/АВ = v/V₁.

У нас вдруг появилось сразу три формулы! Может быть удастся что-нибудь из них найти? Посмотри, что нам известно из условия.

Мы знаем ширину реки АА₁ = 800 м, мы знаем скорости v = 1 v/c и V = 4 м/с. Если эти данные подставить в первую формулу, то получим 800/ВА₁ = 4/1. Отсюда находим, что ВА₁ = 800/4 = 200 м. Но ВА₁ это и есть то самое расстояние, на которое будет снесен катер течением вдоль берега! Получается, что мы нашли то что нам было нужно, хотя вроде бы и не пытались это искать! Всегда бы так.

Задача №13.

Условие:

Лодка, движущаяся относительно воды со скоростью 18 км/ч, должна переправиться через реку шириной 220 м по кратчайшему пути. Сколько времени займет переправа, если скорость течения 2 м/с?

Решение.

Итак, прочитали условие. О чем, о каких телах, объектах в задаче идет речь? Читаем еще раз и выделяем для себя основные термины (слова), которые обозначают эти объекты (тела, вещи): "лодка, вода, река, путь, переправа". Сразу представим себе, что такое для нас лодка - это просто точка, которая движется по поверхности воды; вода, река - это широкая полоса между двумя берегами, которая движется (течет) в какую-то сторону. Нам не сказано, в какую именно сторону течет река, значит куда хотим, туда и направляем, пусть течет в правую сторону. Переправа - это значит передвижение (перемещение, переплывание) с одного берега на другой. Сейчас еще раз прочитаем условие, поймем, что с этими телами происходит, чем они описываются (характеризуются, попросту говоря, что у них есть) - и затем нарисуем чертежик, который поможет нам зрительно (наглядно) представить всю задачу (ситуацию, которая в ней описана).

Продолжаем анализ. Что есть? Есть лодка. Что с ней происходит? Она движется. Что у нее есть? У нее есть скорость. Что можно сказать про ее движение, как она движется? Читаем "по кратчайшему пути". Как же это? Пора рисовать картинку. Два берега, никто не мешает нам нарисовать их просто двумя параллельными прямыми. Между ними, естественно, вода, т.е. река. Лодка отходит от одного берега, например, из точки А.

В курсе геометрии вы когда-то доказывали, что кратчайшее расстояние от точки до прямой есть перпендикуляр, проведенный из этой точки на данную прямую. Можно не помнить это доказательство, из рисунка и так видно, что расстояние от точки А до точек С и D больше чем расстояние до точки В. Отрезок АВ проведен перпендикулярно к берегам, и любое отклонение от него в левую или правую сторону приводит к более длинному пути. Значит, в соответствии с условием задачи, лодка должна плыть в точности по отрезку АВ. Точкой L на рисунке обозначено одно из возможных положений лодки (все остальные положения тоже лежат на отрезке АВ).

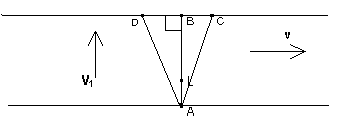
 Что еще есть у лодки, что ее описывает, характеризует? Раз тело движется, то значит у него есть скорость. Двигаются река, и лодка, значит скорость есть и у реки, и у лодки. Причем нам даже сказано в условии, что "скорость лодки относительно воды равна 18 км/ч", а "скорость реки - 2 м/с". Ничего не поделаешь, придется вспоминать, что же мы знаем про скорость вообще. Вспоминать нужно очень тщательно, мы ведь пока не знаем, что за информация (какое именно знание) может нам пригодиться при решении задачи. Если вдруг мы что-нибудь важное не вспомним, то и задачу не решим.

Итак, скорость - векторная величина, имеет какое-либо значение (число) и обязательно куда-то направлена (имеет направление, рисуется как стрелка). Понятно, что раз река течет у нас вправо, то ее скорость направлена туда же, т.е. вправо (это стрелка с буквой v рядом с ней). Это значит, что человек, который стоит на берегу, глядя на палочку, плывущую по течению, увидит как она неторопливо проплывает мимо слева на право. Можно сказать, что стрелка v изображает скорость течения реки относительно берегового наблюдателя, или, коротко, относительно берега. Замечательное дело, рисовали скорость реки, а заодно вспомнили, что скорость, величина ОТНОСИТЕЛЬНАЯ! Разные наблюдатели будут видеть разное движение одного и того же тела. Например, если по реке плывет плот с человеком, то палочка, плывущая мимо берега, будет покоится рядом с плотом. У одной и той же палочки скорость относительно берега будет равна 2 м/с (как скорость воды, мотора ведь у палочки нет), а ее скорость относительно плота будет равна нулю (сколько бы человек на плоту на нее не смотрел, он не будет двигаться мимо него).

Тот же самые береговой наблюдатель глядя на лодку будет видеть, как она плывет в точности по прямой АВ. Значит, скорость лодки относительно берега направлена от точки А к точке В. Изобразим скорость лодки относительно берега стрелкой с буквой V₁ рядом с ней. Знаем ли мы значение этой скорости? Нет, не знаем - в условии задачи сказано, что 18 км/ч - это скорость лодки относительно воды, а мы нарисовали скорость лодки относительно берега. Скорость лодки относительно воды - это такая скорость, которую измерит человек, движущийся вместе с водой и глядящий на переправляющуюся лодку. Например, это может быть человек, стоящий на плоту. Если он теперь будет смотреть не на палочку, а на лодку, то он увидит, что та одновременно и удаляется то него (так как он удаляется от нее), и перемещается в сторону (от одного берега к другому). Если смотреть на рисунок, то такое движение можно было бы изобразить стрелкой, направленно примерно из правого нижнего угла в левый верхний. В этом не будет ничего удивительного, если мы вспомним, что для относительного движения всегда можно применить закон сложения скоростей. В нашей задаче есть три главных тела: лодка, вода и берег. По закону сложения скоростей, скорость лодки относительно берега равна векторной сумме скорости лодки относительно воды и скорости воды относительно берега. Ничего не поделаешь, нужно знать, что такое векторная сумма и как она находится.

Обозначим скорость лодки относительно воды буквой V₂. Тогда, в соответствии с законом сложения скоростей, мы можем написать:

V₁ = V₂ + v

(скорость лодки относительно берега = скорость лодки относительно воды + скорость воды относительно берега). Смысл закона понятен: если бы вода не текла (в озере было бы v = 0), то лодка двигалась бы одинаково что относительно воды, что относительно берега (V₁ = V₂). В реке же лодку еще сносит водой, т.е. добавляется еще ее скорость. Самое главное не забывать, что скорость - это не число, а вектор, т.е. стрелка! Значит складываться должна не числа, а стрелки. Из трех стрелок V₁, V₂ и v у нас нарисованы пока только две (V₁ и v). А известны по условию нам значения скоростей V₂ и v. Заметьте, что мы до сих пор вообще не вспоминали о том, что нужно найти в задаче. Мы просто пока анализировали саму ситуацию, о чем идет речь, что и с чем происходит, что в задаче есть и как это описывается. По ходу дела пришлось вспомнить кое-что из физики и математики (что такое скорость, закон сложения скоростей, кратчайшее расстояние от точки до прямой). Это нормальный и один из наиболее распространенных путей решения задач: забыть на время о том, что нам нужно найти и просто подробно рассмотреть всю ситуацию. Но теперь, пожалуй, наступило время, вернуться к искомой величине. Почему именно теперь? Просто потому, что мы уже очень много для себя прояснили, начертили подробный рисунок, и мы могли бы еще много чего вспомнить. Но стоит ли вспоминать все подряд? Так можно затратить много времени, но не продвинуться к ответу. Мы двигались в неком направлении, которое было задано смыслом условия, теперь пора остановиться, осмотреться и решить, куда же конкретно двигаться дальше. Нашей же конечной целью является искомая величина, значит пришла пора вспомнить о ней. Итак, что же нам нужно найти в данной задаче? Читаем "сколько времени займет переправа?".

Найти время переправы; переправы чего - лодки. Ищем время движения лодки. Откуда до куда - от одного берега до другого. Что мы знаем про движение лодки - она движется по прямой, скорость ее, по идее, все время одна и также. Такое движение, подсказывает нам память, называется равномерным. Очень важный момент, мы проанализировали характер движения лодки, ответили на вопрос "как движется тело". При равномерном движении путь, время и скорость связаны друг с другом формулой (которую мы, конечно же, знаем наизусть)

путь = скорость· время.

В нашем случае путь - это расстояние между берегами, т.е. длина отрезка АВ. Удобно обозначить путь стандартной буквой S; тогда S = AB. Для времени введем букву t. Осталось понять, какая же из трех скоростей (V₁, V₂ или v) должна стоять в этой формуле. Понятно, раз рассматриваем путь лодки, то и скорость должна быть лодки. Дальше просто; раз скорость V₁ направлена в точности вдоль отрезка АВ, то именно эта скорость и должна быть нами использована для вычисления времени.

Нашу формулу теперь мы можем записать в виде

S = V₁ · t.

В этой формуле путь S совпадает с шириной реки, а значит известен по условию: S= АВ = 220 м. Время нам нужно отыскать; выражая время из правой части, получаем t = =S/V₁. Что нам мешает сразу найти время из нашей формулы? Правильно, мы не знаем чему равна скорость V₁. Как только мы ее найдем, сразу же задача будет решена. Значит нам осталось сделать одно последнее усилие, найти скорость лодки относительно берега V₁.

Что мы сделали? Мы остановились, осмотрелись и поняли, в каком направлении должны идти теперь - в направлении отыскания значения скорости V₁. Если бы скорость была не вектором, а числом, то мы легко нашли бы V₁ из формулы V₁ = V₂ + v (ведь значения V₂ и v нам известны). Но все три скорости представляют собой вектор, а вектора складываются геометрически, т.е. с помощью чертежа. Вывод, нам нужен чертеж отдельно для скоростей. Рисуем его, две скорости (V₁ и v) просто перерисовываем с рисунка (начало векторов для удобства берем в одной точке):

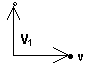
По правилу сложения векторов, суммой двух векторов является такой третий вектор, который соединяет начало первого вектора с концом второго, при условии, что начало второго вектора совпадает с концом первого. Итак, будем разбираться. У нас складываются два вектора V₂ и v. Вектор v уже нарисован, значит удобно считать его первым. Вектор V₂ тогда будет вторым, и его начало должно совпадать с концом вектора v. Значит стрелка V₂ должна выходить из точки · (конец вектора v). Вектор V₁ является суммой v и V₂, значит конец стрелки V₂ должен совпадать с концом стрелки V₁, то есть с точкой ° .

Теперь понятно, как нарисовать вектор V₂: из · в ° . Так и нарисуем

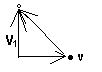
Нам надо найти значение скорости V₁, т.е. длину отрезка V₁. И по условию нам известны длины отрезков V₂ и v. Внимательно смотрим на чертеж и пытаемся понять, что же мы про него знаем. Мы знаем, что v направлена вдоль берега, а V₁ поперек, что между ними угол 90^о (ведь АВ перпендикулярно берегу). Все три стрелки образуют треугольник, один из углов которого прямой (90^о). Значит, мы имеем дело с прямоугольным треугольником! А что же мы знаем про прямоугольные треугольники? Правильно, первое, что приходит на ум, это теорема Пифагора! Квадрат гипотенузы равен сумме квадратов катетов. Отрезки V₁ и v - это катеты, а V₂ - это гипотенуза.

Тогда можем сразу написать: (V₂)² = (V₁)² + v². Находим V₁:

Остальное, как говориться, дело техники. Подставляем значения v и V₂ (не забываем переводить все в систему СИ: v = 2 м/с - это уже система СИ, V₂ = = 18 км/ч = 18· (1000м)/(3600с)= 5 м/с). Находим V₁ = O 21 @ 4,58 м/с.

Наконец, находим искомое время переправы t = 220/4,58 @ 48 с.

Итак, задача решена, ответ: время переправы по кратчайшему пути займет в данных условиях 48 с.

Альманах

Предисловие автора

Небольшое введение для тех, кто только приступает к изучению физики

Список основных определений физических понятий по разделу “Кинематика”

Схема взаимосвязи основных физических величин по разделу “Кинематика”

Задачи на понятия “путь” и “перемещение”

Задачи на прямолинейное равномерное движение

Задачи на прямолинейное равноускоренное движение

Задачи на прямолинейное равноускоренное движение (продолжение 1)

Задачи на прямолинейное равноускоренное движение (продолжение 2)

Задачи на прямолинейное равноускоренное движение (окончание)

Задачи на вертикальное падение

Задачи на вертикальное падение (окончание)

  P.S. Методика организации уроков и примеры используемых дидактических материалов излагаются в файле Методика и дидактика занятий по обучению учащихся искусству решения задач по физике