Задача №4.
Условие.

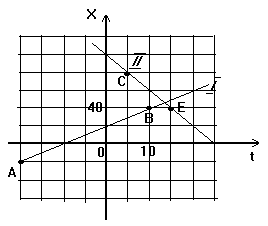
На рисунке даны графики движения двух тел. Написать уравнения их движения. Найти время и место встречи тел. Все величины измеряются в системе СИ.
Решение.
Итак, в этой задаче куда-то, как-то движутся какие-то тела. Вот с чем мы имеем дело. С чего начать наше решение, ведь ничего про эти тела не известно? Во-первых, раз тела движутся, вспомним, что такое движение. В соответствии с пунктом 3, механическое движение (а только такое мы и изучаем) - это перемещение тела в пространстве с течением времени. Это движение можно описать значениями координат тела (пункт 10) в разные моменты времени (пункт 16). Координат у тела может быть три и они обычно обозначаются буквами x, y, и z. Если все три координаты тела меняются, т.е. в разные моменты времени принимают разные значения, то движение очень сложное (например, муха метается по комнате, когда мы пытаемся пристукнуть ее газетой). Если меняются только две координаты, а у третей координаты остается все время одно и то же значение, то тело движется в плоскости (например, муравей ползет по плоской стене). Если же меняется только одна координата, то движение является прямолинейным, т.е. тело движется по прямой (тот же муравей, но теперь он ползет по крепко натянутой бельевой веревке). Если меняется только одна координата, то значения остальных координат для нас не важны. А ту самую изменяющуюся координату мы можем обозначить как нам в голову придет, например x. Таким образом, при прямолинейном движении только одна координата x зависит от времени (обозначим значения времени буквой t, его мы измеряем с помощью секундомера. Когда мы нажали на кнопку и включили секундомер было время t = 0; за секунду ДО этого время было t = -1, а через секунду ПОСЛЕ t =1; и так далее). Если от времени (t) зависит только одна координата (x), то это означает, что движение тела прямолинейное, т.е. происходит по прямой. Вдоль этой прямой (вдоль дороги, например, по которой едет машина) мы положили линейку, написали на ней букву x и смотрим на тело. Число, написанное прямо под телом и которое мы видим на линейке - это и есть координата тела (x). А если одновременно, другим глазом, мы смотрим на часы, то видим значение времени (t).
В нашей задаче есть два тела, но оба они движутся вдоль одной примой (например, вдоль одной дороги). Почему вдоль одной? Потому что на чертеже координаты и того и другого тела обозначены одной и той же буквой (х). Это и означает, что тела двигаются вдоль одной линейки. Для тела с номером 1 нарисована прямая I, которая проходит через точки А и В. Для тела с номером 2 нарисована прямая II, которая проходит через точки С и Е. Если посмотреть на прямую I, то мы увидим, что чем больше время (вправо по оси t), тем больше значение координаты (вверх по оси x). Давайте нарисуем дорогу и линейку. Тогда первое тело с течением времени двигается вдоль линейки в сторону увеличения координат (на нашем рисунке вправо, по стрелке №1). Второе же тело свою координату уменьшает (сначала были большие значения, больше 40, а потом, когда время подошло много за 10, координаты у второго тела стала явно меньше 40). Это означает, что второе тело движется против направления стрелки оси x (на нашем рисунке влево, по стрелке №2). Иначе говоря, тела движутся навстречу друг другу.
Кроме чертежа у нас нет ничего. Значит, всю информацию мы должны взять из него. Посмотри сначала на первую прямую. Она начинается в точке А. Если из этой точки опустить на оси t и x перпендикуляры, то получим два числа: на оси x число -20, а на оси t число -20 (кому непонятно, как эти числа были найдены, посмотрите задачу №1 или напишите мне). Так как t обозначает время, а буква x координату в этот момент времени, то первое тело в момент времени -20 секунд имело координату -20 метров. Как может быть -20 секунд? Да очень просто. Так как начало отсчета времени - это момент, в который мы включили секундомер (пункт 15), то -20 секунд - это за 20 секунд до того как мы включили секундомер. А -20 метров - это (на нашем рисунке) на двадцать метров левее начала линейки (т.е. точки, рядом с которой написан ноль). Итак, первое тело в момент -20 имело координату -20. Это же самое тело спустя некоторое время имело уже другую координату (ведь оно двигалось). Например, по точке В на графике мы видим, что в момент времени 10 у этого тела была координата 40. (Здесь нужно обратить внимание, что график зависимости координаты от времени и рисунок движения тела - это вещи разные. Ось x на графике, и ось x на рисунке - это не одно и то же. На рисунке ось x - это фотография линейки, которую мы сами положили вдоль дороги. На графике ось - это математическая ось, ее называют "ось ординат". Ось t на графике - это тоже только математическая ось, ось абсцисс. А на рисунке оси t вообще не может быть, ведь мы не можем сфотографировать время! Если очень нужно, мы можем рядом с линейкой положить часы и сфотографировать их, но это так и останутся часы, а рядом тело №1, дорога, линейка, тело №2 - все то, что мы можем видеть реально.)
Изучаем чертеж дальше. Прямая I идет таким образом, что при смещении вдоль оси t влево на две клеточки, мы, двигаясь по этой прямой, смещаемся вдоль оси x вверх на одну клеточку. За равные промежутки времени тело №1 проходит равные расстояния. Это означает, что тело №1 движется равномерно! (Смотрите пункт 20). Координата тела при равномерном движении меняется с течением времени по закону x = xo + v· D t (пункт 21), где xo - значение координаты в начальный момент времени (когда мы включили секундомер), v - скорость движения тела, x - значение координаты в момент времени t (так как мы отсчитываем время от нулевого значения, то t = D t). Мы не знаем ни скорости v, ни начальной координаты xo. Зато нам известно, что при t = -20 было x = -20, а при t =10 было x = 40. Закон x = xo + vt должен выполняться ДЛЯ ЛЮБЫХ моментов времени. Для любых - значит и для этих двух. Тогда мы можем вместо x и t подставить в закон равномерного движения их численные значения, от этого тождество не нарушится! Подставляем и получаем: если использовать значения точки А имеем -20 = xo + v(-20), если использовать значения точки В имеем 40 = xo + v10. В результате у нас появилось два уравнения с двумя неизвестными. Решать такую систему уравнений будем
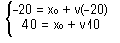
самым универсальным способом. Выразим из первого уравнение одно неизвестное и подставим его в другое. Итак, из первого уравнения имеем xo = -20 - v(-20) = -20 + 20v. Вместо xo во второе уравнение подставляем то, чему он равен в соответствии с первым уравнением и получаем, 40 = -20 + 20v + 10v = -20 + 30v. Тогда, 40 + 20 = 30v, т.е. 60 = 30v. Откуда находим скорость v = 60/30 = 2 м/с. Подставляем найденное значение v в формулу для xo и находим xo = -20 + 20v. = -20 + 20· 2 = 20 м. Мы нашли, что первое тело двигалось вдоль прямой со скоростью 2 м/с, что в начальный момент времени его координата была равна 20 м, и что уравнение его движения x = 20 + 2t (это мы получили, подставив в общую формулу x = xo + vt вместо букв xo и v найденные нами численные значения для них).
Действуя полностью аналогичным способом, разбираемся со вторым телом. Уравнение его движения тоже должно получиться из прямой, только теперь это прямая II. Эта прямая проходит через точки С и Е. По точке С мы находим, что в момент времени 5 второе тело имело координату 80, а по точке Е находим, что в момент времени 15 второе тело имело координату 40. Так как графиком движения второго тела опять является прямая (как и у первого), то значит и второе тело за равные промежутки времени проходит равные расстояния, значит и второе тело движется с постоянной скоростью (равномерно), значит и для второго тела нужно писать уравнение движения в виде x = xo+ vt. Используя данные точки С в этом уравнении, получим формулу 80 = xo + v5, а используя данные точки Е, получаем формулу 40 = xo + v15. Опять мы имеем систему уравнений. Из первого находим xo = 80 - 5v, что дает во втором уравнении 40 = 80 - 5v + v15 = 80 + 10v. Отсюда находим скорость движения второго тела: v = (40 - 80)/10 = - 4 м/с. Знак "минус" указывает на то, что тело движется против направления оси. Для начальной координаты второго тела находим xo = 80 - 5(-4) = 100 м. Окончательно получаем уравнение движения второго тела в виде x = 100 - 4t.
Вот мы и нашли самое главное - уравнения движения обоих тел. Для первого тела имеем уравнение x = 20 + 2t, для второго тела имеем уравнение x = 100 - 4t. Осталось найти время и место встречи этих тел.
Что же такое "встреча"?. В момент встречи тела "наезжают" друг на друга, их положение становится неотличимым, т.е. их координаты совпадают. На чертеже видно, что есть одна точка, в которой координаты тел совпали - это точка пересечения прямых I и II. Во всех остальных точках значения координат тел разные. Таким образом, точка пересечения прямых на чертеже обозначает место и время встречи тел на дороге (т.е. на рисунке). Конечно, можно попытаться найти значения времени и координаты встречи прямо из чертежа, но это может оказаться не совсем точно. Есть универсальный способ нахождения времени и места встречи тел, которым мы сейчас и воспользуемся. Так как в момент встречи координаты тел совпали (xпервого тела = xвторого тела = xвстречи), то мы можем ДЛЯ ЭТОГО момента времени (tвстречи) приравнять правые части уравнений:
20 + 2 tвстречи = 100 - 4 tвстречи.
Из этого уравнения находим tвстречи = (100 - 20)/(2 + 4) = 13, (3) с. Наконец, подставляя значение времени встречи в уравнение движения любого тела, получаем координату места встречи xвстречи = 20 + 2· 13,(3) = 46,(6) м (проверьте сами, что из уравнения движения второго тела получится то же самое значение).
Задача № 5.
Условие.
Автомобиль первую половину времени ехал со скоростью v1 = 10 м/с, а вторую половину времени со скоростью v2 = 15 м/с. Найдите среднюю скорость на всем пути.
Решение.
Итак, мы имеем дело с телом, которое движется. По условию есть ДВА разных участка движения: на одном скорость была равна 10 м/с, а на другом 15 м/с. Определим характер движения. На каждом из участков по отдельности скорость оставалась постоянной. Значит, на каждом участке происходило равномерное движение. Параметры, которые описывают равномерное движение - скорость, время, путь. Смотри на схему и видим, что эти величины (№№ 16, 19, 21) должны быть связаны друг с другом (есть линии 19-21 и 16-21). Смотрим на список - эти линии изображают формулу s = vt. Итак, у нас появилась формула которую можно использовать. Только делать это нужно аккуратно, ведь у нас есть два разных участка движения, значит есть две скорости, два пути и два времени. Чтобы нам было легче, нарисуем чертеж, на котором обозначим все эти величины: s1 и s2 - пути, пройденные телом на первом и втором участках; t1 и t2 - время движения на первом и втором участках; s - общий пройденный путь, который складывается из путей обоих участков; t - общее время движения, которое складывается из времен движения на каждом участке. (Обратите внимание, что во всех задачах мы строго придерживаемся правила "разные величины должны обозначаться по разному". Разные - значит чем-то отличающиеся, например, телом, участком, моментом времени, местоположением, значением и т.п.).
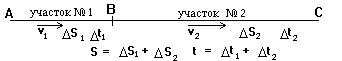
Для КАЖДОГО участка движения можно использовать формулу равномерного движения, значит мы можем записать D s1 = v1 D t1 и D s2 = v2 D t2. Для всего пути мы такое равенство записать не можем, так как на всем пути в целом движение шло с изменяющейся скоростью (сначала 10, потом 15 м/с), т.е. не равномерно. Еще одно соотношение мы можем выписать исходя из того, что в условии сказано, первый участок движения занимал половину времени, а второй тоже половину.
Значит D t1 = D t2 = t/2.
Теперь, когда мы извлекли из условия все, что только можно, вспомним, наконец, что же нам нужно найти. Ищем, оказывается, среднюю скорость. А что это такое? Заглянем в наш список: там есть средняя скорость (№17) и средняя путевая скорость (№18). Какая же из них подразумевается в нашей задаче? Если в условии не говориться о направлении движения тела, значит оно не существенно, значит перемещение нас не интересует, а важным является только путь. Это говорит о том, что подразумевается средняя путевая скорость. По схеме видно, что она (№18) связана с путем (7) и временем движения (16). Формула связи vсп = s/t, где s - весь пройденный телом путь; t - все затраченное на этот путь время. Что ж, подставляем и вычисляем:
vсп = s/t = (D s1 + D s2)/( D t1 + D t2) = (v1 D t1 + v2 D t2)/t = (v1t/2 + v2t/2)/t = t(v1/2 + v2/2)/t = v1/2 + v2/2 = (v1 + v2)/2 = (10 + 15)/2 = 25/2 = 12,5 м/с.
Задача № 6.
Условие.
Автомобиль первую половину пути ехал со скоростью v1 = 10 м/с, а вторую половину пути со скоростью v2 = 15 м/с. Найдите среднюю скорость на всем пути.
Решение.
Задача почти не отличается от предыдущей: только слово "времени" заменено на слово "пути". Все остальное точно также: тело, два участка движения, на каждом участке равномерное движение и найти среднюю скорость. Как мы уже говорили, подразумевается средняя путевая скорость. Все необходимые обозначения и формулы у нас есть. Даже чертеж почти такой же как в задаче №12 (только нужно отметить половины пути).
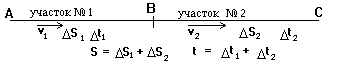
По условию теперь D s1 = D s2 = s/2.
Ищем среднюю путевую скорость: vсп = s/t = (D s1 + D s2)/( D t1 + D t2). В предыдущей задаче у нас были равные времена движения, поэтому мы их в формуле оставили, а от путей избавились с помощью формул D s1 = v1 D t1 и D s2 = v2 D t2. Теперь у нас равные пути, значит избавляться нужно от не одинаковых времен. Мы можем сначала выразить эти времена D t1 = D s1/v1 и D t2 = D s2/v2. Теперь подставляем их в формулу для средней путевой скорости: vсп = s/t = (D s1 + D s2)/( D t1 + D t2). = (D s1 + + D s2)/( D s1/v1 + D s2/v2 ).
Так как D s1 = D s2, то вместо D s2 подставим везде D s1, что даст
vсп = (D s1 + D s1)/( D s1/v1 + D s1/v2 ) = (2 D s1/ D s1)/ ( 1/v1 + 1/v2 ) = 2/(1/v1 + 1/v2) =
= 2/(1/10 + 1/15) = 12 м/с.
Самым любопытным предлагаю доказать, что в этой задаче vсп = 2v1v2/(v1 + v2)!
Небольшое введение для тех, кто только приступает к изучению физики
Список основных определений физических понятий по разделу “Кинематика”
Схема взаимосвязи основных физических величин по разделу “Кинематика”
Задачи на понятия “путь” и “перемещение”
Задачи на закон сложения скоростей
Задачи на прямолинейное равноускоренное движение
Задачи на прямолинейное равноускоренное движение (продолжение 1)
Задачи на прямолинейное равноускоренное движение (продолжение 2)
Задачи на прямолинейное равноускоренное движение (окончание)
Задачи на вертикальное падение
Задачи на вертикальное падение (окончание)
P.S. Методика организации уроков и примеры используемых дидактических материалов излагаются в файле Методика и дидактика занятий по обучению учащихся искусству решения задач по физике