Задача №14.
Условие.
Поезд через 10 с после начала движения приобрел скорость 0,6 м/с. Через сколько времени от начала движения скорость поезда равна 3 м/с?
Решение.
С чем имеем дело? С движущимся телом (поездом). Какие параметры его характеризуют? Из условия видно сразу, что есть следующие параметры: начало движения, момент времени 10 с, конечный момент времени (который надо найти), скорость в первый момент времени (0,6 м/с) и скорость в конечный момент времени. Каков характер движения? По условию скорость в разные моменты времени РАЗНАЯ! Начало движения - это когда тело тронулось с места, т.е. из состояния покоя (т.е. имело скорость равную нулю). Затем скорость за 10 с увеличилась до 0,6 м/с, а затем за какое-то время еще возросла до 3 м/с. Итак, скорость в течение времени движения НЕ ПОСТОЯННАЯ величина, значит движение НЕ РАВНОМЕРНОЕ. Но тогда какой? В задачах, где тело движется с переменной скоростью движение всегда ПОДРАЗУМЕВАЕТСЯ равноускоренным (в противном случае всегда написаны какие-то слова о том как конкретно движется тело). В нашей задаче ничего специально о характере движения тела не написано, значит мы принимаем его равноускоренным (поезд разгоняется, отходя от станции).
Запомнили: если скорость не меняется - движение равномерное, если скорость меняется - движение равноускоренно (если нет специальных слов о движении).
Кроме того, РАЗ НИЧЕГО ДРУГОГО НЕ СКАЗАНО, то мы предполагаем движение прямолинейным (вдоль одной прямой). Полная характеристика движения нашего тела тогда такова - прямолинейное равноускоренное движение.
Выяснив характер движения, начинаем вспоминать:
1. какие важные физические величины описывают такое движение;
2. какие из этих величин друг с другом связаны;
3. как эти величины связаны друг с другом.
Для этого у нас есть наш список и наша схема, на которые мы внимательно смотрим. Итак, пункт 24 напоминает нам, что равноускоренное движение - это движение, при котором скорость тела за равные промежутки времени изменяется одинаково. Пункт 25 говорит о том, что при равноускоренном движении появляется еще одна физическая величина, которая его описывает - ускорения, и что ускорение, скорость и время движения связаны друг с другом. Пункт 28 показывает нам, что перемещение (которое есть у движущегося по прямой тела) при равноускоренном движении связано со скоростью, ускорением и временем движения. Наличие связей между величинами явно показано на схеме.
Выпишем, наконец, формулы прямолинейного равноускоренного движения (которые нужно просто знать наизусть: если в задаче скорость меняется - почти всегда пишем формулы равноускоренного движения).
Обозначим (как это обычно делается) to = 0 -начало отсчета времени, оно же время начала движения; vo - начальная скорость (скорость в тот момент, когда включили секундомер, в нашей задаче vo = 0); t = D t - время движения (показания секундомера в тот момент, когда мы посмотрели на него в следующий раз после включения); v - значение скорости в момент t; D s - значения перемещения тела за время t; а - ускорение тела.
Тогда эти величины связаны друг с другом следующими ДВУМЯ формулами:
v = vo + аt и D s = vo t + a t2/2 .
Отметьте у себя в памяти, что равномерное движение описывается одной формулой (s = vt), а равноускоренное двумя. Причем, ни одна из этих двух формул не похожа на формулу равномерного движения.
Мы проанализировали характер движения, написали ОБЩИЕ формулы, которые справедливы для такого движения, что же дальше? Теперь пора ПРИМЕНИТЬ эти общие формулы к КОНКРЕТНОЙ ситуации нашей задачи, т.е. к конкретным моментам времени, о которых в задаче идет речь. А для этого нам, как всегда, понадобится чертеж.
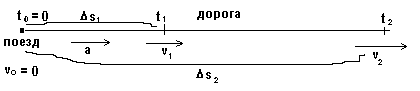
Давайте нарисуем наглядное изображения того, что в задаче происходит.

В начальный момент времени поезд покоился (vo = 0). Под действием ускорения а поезд начал разгоняться и через время t1 приобрел скорость v1, переместившись при этом на D s1. Через время t2 ПОСЛЕ НАЧАЛА ДВИЖЕНИЯ (а не после t1 !) поезд приобрел скорость v2, переместившись при этом на D s2 (от НАЧАЛЬНОЙ точки!). После начала движения у нас в задаче есть ДВА важных момента времени, значит ДЛЯ КАЖДОГО из них нам необходимо записать формулы равноускоренного движения. Записываем: (v0 = 0 не пишем): v1 = аt1, D s1 = a t1 2/2; v2 = аt2, D s2 = a t2 2/2 .
Теперь, после того как все возможные формула написаны, остался последний этап - найти их этих формул искомую величину. Самый простой путь сделать это - подставить в эти формулы ВСЕ известные по условию данные (удобно в системе СИ): v1 = 0,6; t1 = 10; v2 = 3. Подставляем, получаем:
0,6 = а· 10; D s1 = a 10 2/2;
3 = аt2; D s2 = a t2 2/2 .
Как только мы проделали эту процедуру, все стало ясно. Из первой формулы находим, что а = 0,6/10 = 0,06 м/с2. Из третьей формулы находим t2 = 3/а = 3/0,06 = 50 с.
Собственно, задача решена, то что нужно было найти мы нашли. Отметьте только, что в условиях этой задачи можно найти и другие величины: например, из второй формулы находится D s1 = 0,06 10 2/2 = 3 м; из четвертой находится D s2 (сосчитайте сами).
Задача № 15.
Условие.
По заданным на рисунке графикам ускорения построить графики скорости и перемещения (движение считать прямолинейным, начальную скорость считать нулевой, все величины даны в системе СИ). Написать уравнения для скорости и перемещения. Найти путь и перемещение за 3 секунды от начала движения.
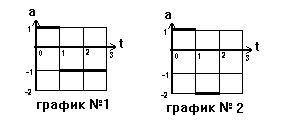
Замечание в скобках условия задачи обычно не пишется, а подразумевается, так что решающему нужно самому догадаться об этом.
С чем имеем дело? На графиках даны значения ускорений в определенные моменты времени. Видимо, какое-то тело (не важно какое) движется ускоренно, по прямой, без начальной скорости. Рассмотрим сначала первый график.
На промежутке времени от ноля до единицы, т.е. в течение первой секунды движения, ускорение было все время равно 1 м/с2. Значит, в течение первой секунды тело двигалось с постоянным ускорением, т.е. равноускоренно! Мы определили характер движения. А знание характера движения сразу позволяет написать нам формулы для движения этого типа. Для равноускоренного движения мы должны написать две формулы (вспоминайте предыдущую задачу) v = vo + а D t и D s = vo D t + a D t2/2. Из графика видно, что движение нашего состоит из двух участков: на первом ускорение равно 1 м/с2, а на втором ускорение равно -1 м/с2 (этот участок длиться две секунды; начинается в момент равный 1 и заканчивается в момент равный 3). В течение второго промежутка времени ускорение тоже не меняет своего значения, значит и на втором участке движение равноускоренное и описывается теми же двумя формулами.
Сначала разберемся с первым участком. Он начинается в момент 0 и заканчивается в момент 1. В начальный момент скорость равна 0 (по условию), значит через секунду она будет равна v = 0 + 1· 1 = 1 м/с. График скорости тела на первом участке движения должен иметь вид прямой, которая выходит из значения 0 и приходит в значение 1. (Почему прямая? Потому что из математики мы знаем, что уравнение вида v = vo + а D t - это уравнение прямой, только на уроках математики мы его записывали через другие буквы, y = kx + b. Но если вместо y написать v, вместо в написать vo, вместо x написать D t, и вместо k написать a, то как раз и получим уравнение скорости при равноускоренном движении). Нарисуем график скорости на первом участке движения.
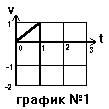
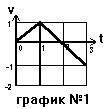
Второй участок движения начинается в момент 1. Скорость тела в момент 1 равна 1 (Это мы только что нашли. Вообще, конечная скорость первого участка является начальной скоростью второго, так как конечный момент первого участка является начальным для второго). Второй участок движения длится две секунды. Ускорение на втором участке движения равно -1. Значит, для второго участка движения мы имеем v0 = 1, t = 2, a = -1. Тогда для скорости в конце второго участка движения мы получим v = 1 + (-1)· 2 = 1 - 2 = -1 м/с. График скорости тела на втором участке движения будет иметь вид прямой, которая начинается в значении 1 (в момент времени 1) и заканчивается в значении -1 (в момент времени 3). Тогда общий график (нарисуем сразу его) будет для первого тела иметь вид.
Разобравшись с графиком скорости, приступим к построению графика перемещения первого тела. Опять нужно по отдельности рассмотреть два участка движения. На каждом из них движение равноускоренное. Значит на каждом из них для перемещения можно применить формулу
D s = vo D t + a D t2/2.
Сперва рассмотрим первый промежуток времени, который длится одну секунду, начинается в момент 0 и заканчивается в момент 1 (обратите внимание, что момент времени и промежуток времени - это величины разные, что я стараюсь все время подчеркивать; однако, на первом участке движения t = D t). Для первого участка движения мы уже знаем, что v0 = 0, t = 1, a = 1. Тогда D s = 0· 1+ 1· 12/2 = 0,5. Значит, график перемещения - это линия (не прямая!), которая выходит из ноля и приходит в 0,5. Что же это за линия?
Из математики мы знаем, что уравнение такого вида: y = a x2 + b x + c - описывает параболу. Ветви такой параболы идут вверх, если а > 0 и идут вниз при а < 0. Если же мы сделаем такие замены: y на D s, x на t, с = 0, а заменим на а/2, то из уравнения параболы получим уравнения для перемещения при равноускоренном движении (только слагаемые нужно еще поменять местами, но от этого равенство не нарушается). Значит, на графике перемещения должна быть нарисована парабола. Так как коэффициент при D t2 положителен (это 1/2), то ветви параболы идут вверх. И, как мы уже нашли, идет эта парабола от значения 0 (при t = 0) до значения 0,5 (при t = 1). Рисуем.
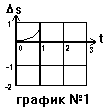
Движение на втором участке начинает из точки, в которой закончился первый. Для второго промежутка времени мы имеем v0 = 1, D t = 2, a = -1. Тогда для значения перемещения, которое было совершено телом в течение второго промежутка времени получим:
D s = 1· 2 + (-1) · 22/2 = 2 - 2 = 0.
В течение промежутка времени от момента 1 до момента 3 перемещения не произошло! Как же так, тело двигалось, а перемещения не произошло?! Да очень просто - это означает, что тело вернулось в ту же точку, из которой оно вышло. А вышло оно из точки со значением 0,5, значит и вернется в точку со значением 0,5. Таким образом, график перемещения на втором участке движения будет иметь вид кривой (параболы!), которая выходит из значения 0,5 (при t = 1) и входит снова в значение 0,5 (при t =3). Так как ускорение теперь отрицательно, то коэффициент при t 2 меньше ноля и ветви параболы идут вниз. Рисуем.
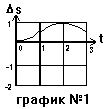
Как на графике скорости, так и на графике перемещения имеется еще одна интересная точка, которая соответствует моменту t =2. Судя по построенным нами линиям, в этот момент времени скорость становится равной нулю, а парабола имеет вершину. Сначала убедимся, так ли это на самом деле. Поскольку, интересующая нас точка принадлежит второму интервалу движения, то мы должны использовать для расчетов значения v0 = 1 и a = -1. Момент времени, который нас интересует, наступил ЧЕРЕЗ секунду после начала второго участка движения, т.е. теперь нужно подставлять D t = 1.
Тогда получим: v = 1· 1 + (-1) · 1 = 0, D s = 1· 1 + (-1) · 12/2 = 1 - 1/2 = 1/2 = 0,5. Итак, скорость в момент 2 действительно равна нулю. Что же это означает? Посмотрим на наши графики. В первую секунду тело разгонялось (ускорение положительное). Затем тело начало тормозить (ускорение отрицательное). Это похоже на автомобиль, который сначала с места начал разгоняться, но вдруг затем резко переключился на задний ход. Никакое тело не может остановиться мгновенно, поэтому оно по инерции еще двигалось перед, пока на мгновение не остановилось (скорость стала равна нулю). Но отрицательное ускорение не исчезло в этот момент времени, значит тело начало двигаться по той же прямой, но вспять, в обратном направлении, стремясь вернуться в исходную точку. Поэтому-то перемещение на втором участке движения некоторое время продолжало увеличиваться, но потом начало уменьшаться до первоначального значения. В тот момент, когда скорость стала равна нулю, парабола достигла своей вершины. Это правило легко запомнить: скорость ноль - у параболы вершина, и наоборот, у параболы вершина - значит скорость ноль (причем, ветви параболы могут идти как вверх, так и вниз).
Чтобы полностью закончить с графиком №1, напишем еще уравнения для скорости и перемещения, и найдем полный путь и полной перемещение, сделанное телом за три секунды.
На первом участке движения скорость подчиняется уравнению v = v0 + aD t = v0 + at, где начальная скорость v0 = 0, t = D t, а ускорение а = 1. Уравнение скорости позволяет найти нам значение скорости в любой момент времени, значит величина t не определена и так и остается символом. Тогда на первом участке имеем уравнение v = t. (так как 0 + 1· t = t). Первый участок движения ограничен моментами от ноля до единицы, значит пишем окончательно: v = t, при 0 < t < 1. Сразу напишем уравнение для перемещения: D s = vo t + a t2/2 = 0· t + 1· t2/2 = t2/2 = = 0,5 t2. Итак: D s =0,5 t2 при 0 < t < 1.
Чтобы написать уравнения скорости и перемещения для второго промежутка времени, необходимо учесть, что время t, откладываемое на осях графиков, отсчитывается от начала отсчета (т.е. от 0, от момента нажатия на секундомер). Время же, которое мы использовали в расчета, отсчитывается от начала второго интервала движения (т.е. от 1). Значения этих двух времен отличаются на единицу (D t = t - 1). В тот момент, когда секундомер покажет значение 2, на втором участке движения прошла только одна секунда. Иначе говоря, чтобы найти время движения на втором участке, нужно от времени секундомера отнять секунду (отнять длительность первого участка). Теперь, учитывая эти замечания, и зная, что на втором участке vo = 1, a = -1, можно записать уравнения скорости и перемещения. Для скорости имеем v = 1 + (-1)· (t - 1) = 1 - (t - 1) = 1 - t + 1 = 2 - t. Для значения перемещения нужно еще учесть, что оно отсчитывается от начальной точки, значит чтобы получить общее перемещение, мы должны к перемещению за первый участок движения прибавлять перемещение, которое совершает тело после начала второго промежутка времени.
Тогда пишем D s = 0,5 + 1· (t - 1) + (-1) · (t - 1)2/2 = 0,5 + t - 1 - (t2 - 2t + 1)/2 = - 0,5 t2 + 2 t - 1. Не будем забывать, что эти уравнения справедливы только при 1 < t < 3.
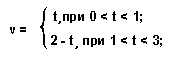
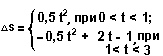
Уравнения для скорости
и перемещения
(график №1).
Теперь находим сами путь и перемещение. Смотри на график перемещения: за первую секунду тело переместилось на 0,5 метра от начальной точки вперед. За вторую секунду оно переместилось еще на 0,5 метра вперед. Всего за две секунды тело переместилось вперед на 1 м (подставьте в уравнение для D s при 1 < t < 3 значение t = 2). За третью секунду тело переместилось на 0,5 метра НАЗАД. Значит полное перемещение будет равно D s = 1 - 0,5 = 0,5 м (подставьте в уравнение для D s при 1 < t < 3 значение t = 3). Путь же - это полное расстояние, пройденное телом за все три секунды, которое складывается из одного метра, пройденного за две секунды до точки останова (где тело повернуло назад) и еще половины метра, которую тело прошло в обратном направлении. Значит путь равен: s = 1 + 0,5 = 1,5 м.
Если вы устали, то перед тем как переходить ко второму графику, лучше немного отдохнуть.
Второй график очень похож на первый: тоже сначала имеем положительное ускорение, затем отрицательное, но вот затем ускорения нет вообще. Значит, в этом случае мы имеем ТРИ участка движения. На первом участке тело разгоняется, на втором тормозит, а на третьем движется без ускорения. Раз ускорения нет, то такое движение происходит с неизменной скоростью, т.е. является равномерным. Итак, третий график описывает движение, состоящее из трех участков: двух участков равноускоренного движения и одного участка равномерного движения. Все необходимые общие формулы мы знаем и сразу их выписываем. Для равноускоренного движения v = v0 + a D t, D s = v0 D t + a D t2 /2, для равномерного движения D s = v D t. Самое главное, аккуратно эти формулы применить для решения нашей задачи.
Рассматриваем первый участок (на нем t = D t). Он начинается при t = 0, заканчивается при t = 1, длится одну секунду, имеет v0 = 0 (по условию) и а = 1 (из графика). Тогда при 0 < t < 1 для скорости и перемещения мы можем сразу записать следующие уравнения: v = v0 + at = 0 + 1t = t (окончательно v = t); D s = v0 t + a t2 /2 = = 0 t + 1 t2 /2 = 0,5 t2 (D s = 0,5 t2). В конечный ДЛЯ ПЕРВОГО УЧАСТКА момент времени t =1 мы получаем значения v = 1 м/с и D s = 0,5 м.
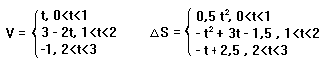
Второй участок начинается тогда, когда закончился первый, т.е. при t = = 1. В начальный для второго участка момент времени мы имеем следующие начальные значения (которые являются конечными для первого участка движения) v = 1 м/с и D s = 0,5 м. Ускорение теперь а = -2. Время движения тела от начала второго промежутка времени на одну секунду меньше времени, которое показывает секундомер (D t = t - 1). А полное перемещение тела складывается из перемещения на первом участке движения и перемещения второго участка. Тогда для скорости и перемещения на втором интервале движения записываем следующие уравнения: при 1 < t < 2 будет v = 1 + + (-2) · (t - 1) = 3 - 2t (окончательно v = 3 - 2t); D s = 0,5 + 1 (t - 1) + (-2) (t - 1)2 /2 = - t2 + 3t - 1,5 (D s = - t2 + 3t - 1,5). Конечные значения скорости и полного перемещения в момент времени 2 (конечное время второго промежутка времени движения) получаем, если в эти уравнения подставить t = 2. Тогда v = -1, и D s = 0,5. Эти численные значения являются начальными для третьего участка движения.
Поскольку в течение всего третьего интервала движения ( 2 < t < 3) скорость меняться не должна (равномерно движение, без ускорения), то скорость все время v = -1. Для перемещения же мы должны использовать формулу равномерного движения. Однако, нужно учесть, что третий участок движения начинается на 2 секунды позже после начала отсчета времени (D t = t - 2), а отсчет перемещения начинается со значения 0,5. Тогда уравнение для перемещения имеет вид D s = 0,5 + (-1)(t - 2) = - t + 2,5. Сведем полученные формулы вместе.
Теперь уже не сложно построить соответствующие графики. На графике скорости мы должны сначала нарисовать прямую, которая из значения 0 (при t = 0) идет в значение 1 (при t = 1), затем прямую из этой точки в точку со значением -1 (при t = 2), после чего продолжить это значение на всю третью секунду движения.
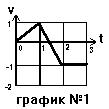
По графику следует ожидать, что при t = 1,5 с скорость станет равной нулю. Проверим это предположение, подставив число t = 1, 5 в формулу для скорости на втором промежутке движение (при 1< t< 2). Действительно, получается ноль. Мы уже знаем, что тогда на графике перемещения в этот момент времени должна быть вершина.
Чтобы нарисовать график перемещения, нужно сначала в течение первой секунды построить параболу ветвями вверх, которая выходит из ноля (при t = 0) и входит в 0,5 (при = 1). Затем из этой точки нужно нарисовать параболу ветвями вниз снова до значения 0,5 (при t = 2). Из этой точки мы должны провести прямую вниз до значения -0,5 ( уравнение вида D S = -t + 2,5 - это уравнение прямой). Тогда получим следующий график.
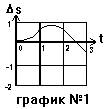
По графику видно, что первые ПОЛТОРЫ секунды тело двигалось вперед (до значения скорости v = 0), а потом еще полторы секунды двигалось в обратном направлении. Общее перемещение равно D S = -0,5 (это конечное значение D S. Чтобы найти путь, мы должны сложить метры, которые тело двигалось вперед (0,75 - это значение D S при t = 1,5), с метрами, которые оно двигалось назад (еще 0,75 до нуля и еще 0,5 до конца). Тогда получим: s = 0,75 + 0,75 + 0,5 = 2 м. Конец!
Небольшое введение для тех, кто только приступает к изучению физики
Список основных определений физических понятий по разделу “Кинематика”
Схема взаимосвязи основных физических величин по разделу “Кинематика”
Задачи на понятия “путь” и “перемещение”
Задачи на прямолинейное равномерное движение
Задачи на закон сложения скоростей
Задачи на прямолинейное равноускоренное движение (продолжение 1)
Задачи на прямолинейное равноускоренное движение (продолжение 2)
Задачи на прямолинейное равноускоренное движение (окончание)