Задача № 16.
Условие.
За какое время автомобиль, двигаясь из состояния покоя с ускорением 0,6 м/с2, пройдет 30 м?
Решение.
Эту задачу с нашим опытом мы сделаем в два счета. С чем имеем дело? С движущимся телом (автомобилем). Какие параметры его характеризуют? Время, ускорение, путь - то, что сразу есть в условии. Каков характер движения? Чтобы ответить на этот вопрос, нужно определить, что происходит со скоростью. Раз есть постоянное ускорение, значит скорость меняется равноускоренно, т.е. движение равноускоренное. Еще нужно определить тип траектории. Раз ничего не сказано, значит подразумевается простейшее движение, т.е. по прямой. Итак, у нас прямолинейное равноускоренное движение. (А если скорость не меняется, какое было бы движение? Правильно, равномерное).
Уточним, все ли существенные величины нами были названы (это нужно делать обязательно, вдруг мы что-то пропустили). Сначала просто вспомним, какие еще физические величины нам встречались в разных ситуациях: это и перемещение, и скорость. Про них в условии ничего не сказано. Значит нам нужно самим определить, существенны ли они или нет. Если окажется, что эти величины СВЯЗАНЫ с теми, которые даны по условию, значит они тоже СУЩЕСТВЕННЫ для нас.
Анализируем условие. Для этого представим себе, что происходит. Автомобиль, разгоняясь с места, движется все время в одном направлении. Путь при прямолинейном движении в одну сторону (без возвратов) совпадает с перемещением. Значит перемещение для нас существенная величина. Перемещение (№28), ускорение (№23) и время движения (№16) связаны на схеме друг с другом (линии 16-28; 23-28). Но из той же схемы мы видим, что эти величины связаны еще и №25 (линии 23-25, 16-25), который (как видно из списка понятий) соответствует скорости. Значит, к тем величинам, которые существенны для нашей задачи и явно даны в условии нужно добавить еще скорость. Полный набор существенных величин состоит, таким образом, из пути (перемещения), скорости, ускорения и времени движения.
Следующий шаг - выписать основные (общие) формулы, справедливые для данного типа движения. Это формулы, которые заданы линиями 16-25, 23-25, 16- -28, 23-28. Находим, что это формулы v = vo + a D t, и D s = vo D t + a D t2 /2. Это две стандартные формулы равноускоренного движения, которые нужно выписывать всегда, когда мы имеем дело с равноускоренным движением. Так как в этой задаче рассматривается только один промежуток времени движения, то нет смысла различать время t и D t, т.е. t = D t.
Следующий шаг - нужно правильно и аккуратно эти формулы применить для решения нашей задачи. Применить - значит подставить в них конкретные значения (или символы, разным величинам разные) физических величин, данные нам по условию, и проделать математический расчет.
У нас в задаче: так как движется автомобиль из состояния покоя, то vo = 0, а = 0,6 м/с2, s = D s = 30 м (все величины даны уже в системе СИ). Подставляем и получаем: v = 0 + 0,6t и 30 = 0t + 0,6 t2 /2. Внимательно смотрим на наши уравнения и ищем, нет ли среди них такого, где осталась ТОЛЬКО ОДНА буква! В первом уравнении после подстановки осталось две буквы: это v и t. Из одного уравнения две неизвестных величины не найти. А вот во втором уравнении осталась только одна буква t! Значит, беремся быстренько за это уравнение: 30 = 0,6 t2 /2 и находим из него t. Вычисления дают:
t2 = 30· 2/0,6 = 100, t = O 100 = 10 с. Задача решена.
Кстати, если теперь подставить t в первое уравнение, то мы сможем найти скорость в этот момент времени. Есть и такие задачи, но хорошо, что не эта. Да, мы совсем забыли нарисовать чертеж! Задача оказалась такой простой, что и без него обошлись. Но, если желаете, пожалуйста!
![]()
Задача №17.
Условие.
Шарик, скатываясь с наклонного желоба из состояния покоя, за первую секунду прошел путь 10 см. Какой путь он пройдет за три секунды? Какой путь он пройдет за третью секунду?
Решение.
Проводим анализ задачи. Тело (шарик) движется. Наш жизненный опыт подсказывает нам, что если шарик поставить на наклонную плоскость и отпустить, он поедет вниз, постепенно разгоняясь. Двигаться будет по прямой, скорость будет расти. Поскольку, мы всегда рассматриваем простейший случай, то будем считать движение нашего шарика прямолинейным и равноускоренным. Этим все сказано. Из анализа предыдущей задачи мы знаем, что для прямолинейного равноускоренного движения важны (существенны) следующие величины: скорость v, время t = D t (один участок движения), перемещение D s, ускорение а. При движении из состояния покоя начальная скорость отсутствует vo = 0. Общие формулы равноускоренного движения имеют вид: v = vo + at, и D s = vo t + a t2 /2. Наша задача - их правильно применить. Нарисуем чертеж.
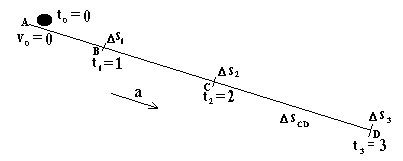
Из точки А из состояния покоя в начальный момент времени начал двигаться шарик с ускорением а. Через одну секунду он дошел до точки В, пройдя расстояние АВ = 10 см. Еще через одну секунду, т.е. через две секунды после начала движения, шарик дойдет до точки С, пройдя расстояние АС. За три секунды движения шарик пройдет расстояние АD, которое нужно найти. Еще нужно найти расстояние, пройденное за третью секунду. Обратите внимание, "за три секунды" и "за третью секунду" - это вещи разные. За три секунды - значит за три секунды, прошедшие от начала отсчета. За третью секунду - значит за интервал времени от начала до конца третьей секунды. Первая секунда началась при t = 0 и закончилась при t = 1 (шарик двигался из А в В). Вторая секунда началась тогда, когда закончилась первая, т.е. при t = 1, и закончилась через секунду, т.е. при t =2 (шарик двигался из В в С). Третья секунда началась при t = 2 и закончилась при t = 3 (шарик двигался из С в D). Значит путь, пройденный за третью секунду - это расстояние CD.
После анализа задачи переходим к непосредственно к решению. Ни в условии, ни в анализе мы не затрагивали скорость движения шарика, везде нас интересовали только перемещение (путь) и время. Можно сделать предположение, что для решения ЭТОЙ задачи формула для скорости нам не понадобиться. Так что ограничимся только формулой D s = vo t + a t2 /2. У нас есть три важных точки: В, С и D. Значит мы должны рассмотреть три важных момента времени: t1, t2 и t3.
Для КАЖДОГО из них мы можем записать нашу формулу (учтем, что vo = 0): D s1 = = a t12 /2, D s2 = a t22 /2, D s3 = a t32 /2. По условию, D s1 = АВ = 10 см, t1 = 1 с, t2 = 2 с и t3 = 3 с. Кроме того, D s2 = АС и D s3 = АD.
Подставляем все численные значения и ищем формулу с одной буквой (!):
10 = a 12 /2, D s2 = a 22 /2, D s3 = a 32 /2.
Есть такая формула в этой строчке! Это самая первая формула, в которой только одна буква - буква а, которая обозначает ускорение шарика. Легко это ускорение находим; а = 20 см/с2. Если найденное ускорение подставить в оставшиеся две формулы, то мы найдем АС = D s2 = 40 см и AD = D s3 = 90 см.
Путь, пройденный за три секунды - это и есть AD = D s3 = 90 см. Путь, пройденный за третью секунду - это CD = AD - АС = 90 - 40 = 50 см.
Задача № 18.
Условие.
От остановки одновременно отходят трамвай и троллейбус. Ускорение троллейбуса в два раза больше ускорения трамвая. Сравнить пути, пройденные за одно и тоже время, и приобретенные ими за это время скорости.
Решение.
В этой задаче рассматривается два движущихся тела. Значит мы должны проанализировать характер движения каждого из них. Это сделать не сложно, так как в условии черным по белому написано "ускорение троллейбуса в два раза больше ускорения трамвая". Тем самым подразумевается, что эти ускорения есть и они не меняются. А движение с постоянным ускорением - это равноускоренное движение. Поскольку же ничего не говорится о виде траектории (не окружность, не кривая), то подразумевается прямолинейное движение. Итак, мы опять имеем дело с прямолинейным равноускоренным движением. Общие формулы для такого движения - v = vo + at, и D s = vo t + a t2 /2 (так как опять в задаче рассматривается только один участок движения, то D t = t).
В начальный момент времени оба тела покоились, так что vo = 0. Но ускорения у этих тел разные, значит скорости и перемещения тоже будут разные (за один и тот же промежуток времени). Разные величины должны обозначаться по разному. Так что все, что относится к троллейбусу мы будем обозначать с номером 1, а все трамвайные величины будем писать с номером 2.
Теперь применим общие формулы к нашей конкретной задаче. Для этого выпишем их для каждого тела по отдельности.
Троллейбус:
v1 = a1 t
D s1 = a1 t2 /2
Трамвай:
v2 = a2 t
D s2 = a2 t2 /2
Нам нужно сравнить скорости и перемещения. В математике сравнить можно двумя способами: найти разность величин (вычесть из одной другую) и найти отношение величин (поделить одну на другую). В физике же слово "сравнить" всегда означает "найти отношение"! Это нужно просто запомнить (объяснение очень простое: не всякие физические величины можно вычитать друг из друга, так как это может привести к неправильному обращению с единицами измерений; но делить друг на друга можно любые физические величины). Значит нам нужно найти два числа: одно неизвестное равно отношению скоростей, другое неизвестное равно отношению перемещений. Находим:
v1 / v2 = (a1 t)/( a2 t) = a1 /a2 ; D s1 /D s2 = (a1 t2 /2) / (a2 t2 /2) = a1 /a2 .
Итак, и отношение скоростей, и отношение перемещений (взятых за один и то же промежуток времени для тел, движущихся из состояния покоя) равно отношению ускорений. Это, конечно, хорошо, но нам то нужно число в ответе! Если мы в результате наших вычислений не получили еще числовой результат, значит мы не использовали еще какую-то информацию, которая была в условии задачи. Вернемся еще раз к условию и снова прочитаем его. Что в нем такого есть, что мы еще не употребили? Там есть число 2. Сказано, что ускорение троллейбуса в ДВА раза больше ускорения трамвая. Мы же это число 2 до сих пор не использовали. Пришла пора и для него поработать на нас. Правда, чтобы решить задачу, нам нужны формулы, а слова "ускорение троллейбуса в ДВА раза больше ускорения трамвая" - это пока только слова. Значит, мы должны превратить их в формулу. Смысл этой фразы прост: если взять ускорение трамвая (а2) и увеличить его в два раза (т.е. умножить на 2), то получим (т.е. можем приравнять) ускорение троллейбуса (а1): 2· а2 = а1. Вот и формула.
Тогда получаем: v1 / v2 = D s1 /D s2 = a1 /a2 = 2.
Задача № 19.
Условие.
Первый вагон трогающегося от остановки поезда проходит за 3 с мимо наблюдателя, находившегося до отправления поезда у начала вагона. За сколько времени пройдет мимо наблюдателя весь поезд, состоящий из 9 вагонов? Промежутки между вагонами можно не рассматривать.
Решение.
Вам не подсказывает интуиция, что эта задача тоже на формулы равноускоренного движения? Мне вот подсказывает, все признаки этого налицо: Движущееся тело (поезд), увеличение скорости (отходит от остановки - значит постепенно разгоняется). Так что сходу пишем v = at, и D s = a t2 /2 (из состояния покоя, значит vo = 0 и D t = t). Чтобы применить эти формулы к нашей задаче, нужно аккуратно проанализировать, что происходит с движущимся телом, какие важные моменты времени, расстояния, скорости нужно выделить. Проделать такой анализ нам всегда поможет рисунок.
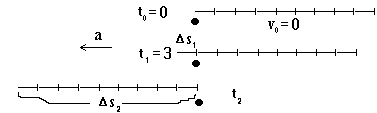
Наблюдатель (шарик) в начальный момент времени (to = 0) стоит у левого конца поезда. Без начальной скорости поезд начинается двигаться влево. За три секунда мимо наблюдателя проезжает первый вагон. Значит к моменту времени t1 = 3 поезд совершает перемещение D s1 равное длине одного вагона. К моменту времени t2 проходит весь поезд, все девять вагонов, совершается перемещение D s2. Скорость нас в этой задаче вроде бы не интересует, так что формулу для скорости не пишем. Зато мы имеем два существенных момента времени (t1 и t2), так что формулу для перемещения нужно написать два раза. Сделаем это: D s1 = a t12 /2 , D s2 = a t22 /2 (вы уже знаете; это означает, что мы приступили к применению общих формул к нашей конкретной задаче). Теперь подставляем данные: по условию дано t1 = 3. Получим D s1 = a 32 /2 , D s2 = a t22 /2. Ищем формулу с одной буквой, ... и не находим. Что делать? Снова обратимся к условию, может мы что-то забыли? В условии есть число 9 (девять вагонов). Это число мы пока не использовали. Если один вагон проходит мимо наблюдателя - поезд совершает перемещение D s1; если девять вагонов проходит - D s2. Понятно, что 9 вагонов - это в 9 раз больше, чем 1. Значит, перемещение D s2 в 9 раз больше чем перемещение D s1. Эти слова можно записать в виде формулы D s2 = 9 D s1. Подставим это выражение вместо D s2, получим 9 D s1 = a t22 /2. Рядом припишем первую формулу D s1 = a 32 /2. Смотрим, все равно нет формулы с одной буквой! Более того, формул две, а букв в них три! Два уравнения с тремя неизвестными - вот что мы имеем! Что же на делать? Условие задачи мы полностью использовали, ситуацию полностью проанализировали - информацию больше брать неоткуда. Так может быть, нам больше ничего и не нужно? А что, если попробовать решать эти уравнения так, как будто нам известно все, что нам хочется? Что нам надо искать, t2? Давайте искать t2! Выражаем искомое время из первой формулы: t22 = 2· 9· D s1 /а.
Если бы мы знали ускорение а и перемещение D s1, мы бы могли сосчитать значение t22. Будем действовать так, как будто мы их знаем!
Берем формулу D s1 = a 32 /2 и используем ее, чтобы избавиться от D s1. Тогда получаем: t22 = 2· 9· ( a 32 /2)/а. Раскройте-ка внимательно эту дробь! Ускорение а сокращается! Хотя мы его не знаем, оно оказывается нам и не нужно! Тогда находим t22 = 2· 9· 32 /2 = 81 и t = O 81 = 9 с.
Задача № 20
Условие.
Во сколько раз скорость пули в середине ствола ружья меньше, чем при вылете из него?
Решение.
Зарядили ружье, нажали на курок, боек ударил по капсюлю, капсюль высек искру, искра воспламенила порох, пороховые газы вырвали пулю из гильзы начали ее разгонять. Нас, конечно, все эти тонкости не интересуют, мы, наученные нашим большим опытом решения задач, сразу видим, что имеем дело с телом, которое начинает двигаться прямолинейно и равноускоренно из состояния покоя. Ну, мне, по крайне мере все признаки "болезни" видны как на ладони, а вам? Если есть у вас на этот счет какие-то сомнения - напишите мне, обсудим.
Имея дело с прямолинейным равноускоренным движением, мы должны использовать для его описания две формулы (в простых задачах иногда достаточно и одной). Чтобы легче было разбираться с рассматриваемой ситуацией, нарисуем чертеж.
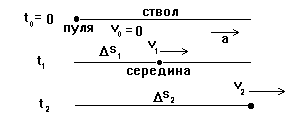
В задаче есть два важных момента времени, значит мы должны выписать формулы равноускоренного движения два раза. В задаче используются все величины (речь идет и о скорости, и о перемещении вдоль ствола), значит нам понадобятся обе формулы. Кроме того, в условии еще упомянута середина ствола, значит нужно вспомнить, что такте середина и как эта информация может быть использована. Теперь, когда в общих чертах мы обрисовали поле нашей ближайшей деятельности, можно приступать к конкретным вычислениям. Сначала выпишем формулы, применив их конкретно к моментам t1 и t2 (t = D t).
t1 ; t2 ;
v1 = at1 (vo = 0) v2 = at2 (vo = 0)
D s1 = a t12 /2 D s2 = a t22 /2.
Сразу запишем в виде формул всю дополнительную информацию.
Середина - это точка, которая делит отрезок пополам, значит D s1 это половина (одна вторая) от D s2 : D s1 = D s2 /2. Теперь мы можем вместо D s1 использовать найденное выражения (кто из читателей дошел до этого места, тот наверняка уже заметили, как часто используется математическое действие ПОДСТАНОВКА. Подстановка - это единственный способ избавляться от неизвестных величин, выражая их через другие). Получим:
t1 ; t2 ;
v1 = at1 (vo = 0) v2 = at2 (vo = 0)
D s2 /2= a t12 /2 D s2 = a t22 /2.
Наша цель, найти, во сколько раз скорость v1 меньше скорости v2, т.е. вычислить отношение v2/v1. Что ж, надо так надо, вычисляем: v2/v1 = at2 / at1 = t2 / t1 . Чтобы избавиться от t2 и t1 придется использовать формулы для перемещений:
v2/v1 = t2 / t1 = Ц (2· D s2 /а) / Ц (D s2 /а) = Ц 2 /Ц 1 = Ц 2 = 1,41.
Итак, скорость пули в середине ствола примерно в 1,41 раза меньше ее скорости при вылете из ружья.
Небольшое введение для тех, кто только приступает к изучению физики
Список основных определений физических понятий по разделу “Кинематика”
Схема взаимосвязи основных физических величин по разделу “Кинематика”
Задачи на понятия “путь” и “перемещение”
Задачи на прямолинейное равномерное движение
Задачи на закон сложения скоростей
Задачи на прямолинейное равноускоренное движение
Задачи на прямолинейное равноускоренное движение (продолжение 2)
Задачи на прямолинейное равноускоренное движение (окончание)