Задача № 25.
Условие.
Зависимость скорости от времени для материальной точки имеет вид v = 2 + 6t. Написать уравнение для координаты, если в начальный момент времени тело находилось в точке с координатой -5 (все величины даны в системе СИ). Найти ускорение тела, путь и перемещение, пройденные им за 10 с.
Решение.
Какие ключевые понятия помогают нам выделить признаки, по которым мы определим характер движения тела? Прежде всего, это “скорость”, “координата”, “ускорение”, “путь”, “перемещение” - они в явном виде присутствуют в условии. Координат у тела может быть три (x, y, z), две (x, y) или одна (x). Раз нам сказано “найти координату” (а не координаты), то значит мы имеем дело с движением вдоль одной прямой (единственное число - одна координата - одна прямая). Итак, движение прямолинейное. Скорость - меняется или не меняется в процессе движения? Ответить на этот вопрос нам поможет уравнение для скорости. Из него мы видим, что в РАЗНЫЕ моменты времени t значения скорости v тоже РАЗНЫЕ. Значит, скорость меняется, значит движение не является равномерны, т.е. скорее всего одно равноускоренное. Для того, чтобы принять окончательное решение о характере движения тела, нужно вспомнить что-либо о свойствах равноускоренного движения и сравнить с нашей ситуацией. Вспоминаем. Ага, вспомнили: при равноускоренном движении справедливы два уравнения (одно для скорости, другое для перемещения), которые имеют вид: v = v0 + a D t, D S = v0 D t + a D t2 /2. В нашей задаче тоже есть уравнение для скорости. Давайте сравним наше уравнение и общее, напишем их рядышком друг с другом и внимательно посмотрим на них:
v = v0 + a D t,
v = 2 + 6t.
Что мы должны обнаружить при СРАВНЕНИИ этих формул? Во-первых, чем они отличаются, а во-вторых, что в них одинакового. Главный вопрос, на который мы должны ответить, можно ли ПРОСТОЙ ПОДСТАНОВКОЙ превратить одну формулу в другую?
Первое, что нужно сказать, что раз в задаче нет различных участков движения, то все времена измеряются от начального времени t0 = 0 и тогда D t = t - t0 = t. Значит, отличие формул еще меньше, чем кажется на первый взгляд:
v = v0 + at,
v = 2 + 6t.
Теперь ясно видно, что если вместо v0 подставить 2, в вместо а подставить 6, то мы из первой формулы сразу получим вторую! Вывод, наша КОНКРЕТНАЯ формула для скорости является ЧАСТНЫМ случаем ОБЩЕЙ формулы для скорости равноускоренного движения. Следовательно, наше тело совершает равноускоренное движение. Причем, мы сразу можем сказать КОНКРЕТНЫЕ значения начальной скорости и ускорения нашего тела: v0 =2 м/с, а = 6 м/с2.
Теперь легко написать остальные конкретные уравнения для движения нашего тела. Чтобы их получить, нужно в общие уравнения равноускоренного движения подставить конкретные значения рассматриваемой частной ситуации. Значит, мы берем уравнение для перемещения D S = v0 D t + a D t2 /2 и вместо D t пишем t, вместо v0 пишем 2, вместо а пишем 6. Получаем D S = 2 t + 6 t2 /2 = 2t + 3 t2. Наша задача - написать уравнение для координаты. Перемещение и координаты связаны, ведь если тело перемещается, то его координаты меняются. Как связаны эти величины? Смотрим в наш список; при прямолинейном движении D S = х - хо, откуда х = хо + D S. По условию начальная координата хо = -5, тогда уравнение для координаты принимает вид х = -5 + 2t + 3 t2. Осталось найти путь и перемещение. Перемещение находится простым вычислением значения D S = 2t + 3 t2 при t = 10: т.е. D S = 2· 10 + 3· 102 = 320 м. Так при своем движении тело двигалось все время в одном направлении (координата только увеличивалась, точек поворота не было и тело назад не возвращалось), то путь будет совпадать с перемещением: S = D S = = 320 м.
Задача № 26.
Условие.
Уравнение движения материальной точки имеет вид x = 2t - 0,2 t2 . Написать уравнение для скорости движения тела, найти ускорение, скорость, путь и перемещение через 8 секунд после начала движения.
Решение.
Для того, чтобы определить характер движения тела, мы в этой задаче имеем только уравнение для его координаты. Значит, мы должны сравнить это уравнение со всеми общими уравнениями движения, которые мы знаем. Нам известны пока лишь два типа движения: равномерное и прямолинейное равноускоренное. Для равномерного движения уравнение координаты имеет вид (это мы находим в списке основных кинематических величин) x = x0 + v D t, но поскольку участок движения у нас в этой задаче один и время отсчитывается от нуля, то D t = t и окончательно x = x0 + v t. Для равноускоренного движения уравнение выглядит следующим образом (смотрите предыдущую задачу, кроме того сразу учитываем, что D t = t) x = xo + vo t + a t2 /2.
Радикальное отличие этих двух уравнений: x = x0 + v t и x = xo + vo t + a t2 /2 заключается в том, что первое уравнение содержит t в первой степени, а второе во второй (t2). Главный отличительный признак - есть или нет в уравнении для координаты квадрат времени: если нет - движение равномерное; если есть - движение равноускоренное! Теперь внимательно глядим на наше конкретное уравнение нашей конкретной задачи. Есть квадрат? Есть! Вывод? Наше тело движется равноускоренно. А так как положение тела описывается только одной координатой, то это движение прямолинейное (вдоль оси координат х).
Прямолинейное равноускоренное движение описывается еще и уравнением для скорости v = vo + at. Чтобы это уравнение записать конкретно для нашей задачи, нужно знать конкретные значения для начальной скорости vo и ускорения а. Откуда мы их возьмем? У нас есть возможность сравнить ОБЩЕЕ и КОНКРЕТНОЕ уравнения для координаты:
x = xo + vo t + a t2 /2
x = 2t - 0,2 t2 .
И то и другое уравнения описывают равноускоренное прямолинейное движение. Просто, первое записано в общем виде (без конкретных чисел), а второе уже с конкретными числами. Чтобы из общего уравнения получить конкретное, нужно вместо букв подставить числа. Спрашивается, вместо каких букв и какие числа нужно подставить в общее уравнение, чтобы из него получилось наше конкретное. Это тест на внимательность. Кто его прошел, тот заметил, что если вместо xo подставить 0 (если величины нет, значит ее значение ноль!), вместо vo подставить 2, вместо a/2 (вот где особая хитрость) подставить - 0,2 (не теряйте знак!), то получим сразу наше конкретное уравнение. Тогда мы можем сделать вывод, что для нашей конкретной задачи имеем: xo = 0, vo = 2, a/2 = - 0,2! Начальная координата равна нулю, т.е. тело в начальный момент времени тело находилось в начале координат. Начальная скорость равна 2 м/с. Половина (!) ускорения равна 0,2 м/с2, значит само ускорение равно а = - 0,4 м/с2. Теперь нам известны все параметры, необходимые для ПОЛНОГО описания равноускоренного прямолинейного движения. Уравнение для скорости принимает вид v = 2 - 0,4t. Итак, для нашего случая уравнения имеют вид: x = 2t - 0,2 t2 , v = 2 - 0,4t. Зная уравнения движения можно найти ВСЕ, что только понадобиться узнать об этом движении.
Через 8 с после начала движения, т.е. при t = 8, координата и скорость будут равны: x = 2· 8 - 0,2· 82 = 3,2 м, v = 2 - 0,4· 8 = -1,2 м/с. Перемещение при прямолинейном движении всегда находится как D S = х - хо = 3,2 - 0 = 3,2 м. Осталось найти путь. Если в процессе движения тело движется все время в одном направлении, то путь совпадает с перемещением. Значит, первое, что мы должны определить, поворачивало ли тело назад или нет в течение нужных нам восьми секунд? Для этого есть несколько способов, но самый универсальный - построить график зависимости координаты от времени и на нем сразу все будет видно. График зависимости координаты от времени при равноускоренном движении имеет вид параболы.
В нашем случае эта парабола описывается уравнением вида x = 2t - 0,2 t2. При квадратичном члене уравнения стоит ОТРИЦАТЕЛЬНЫЙ коэффициент (-0,2), что говорит о том, что ветви параболы идут ВНИЗ!
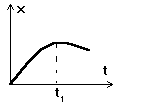
Достаточно нарисовать этот график только схематично, чтобы увидеть наличие точки поворота: до момента времени t1 координата тела увеличивалась, а после этого момента времени стала уменьшаться. Это и означает, что тело повернуло в обратную сторону. Если время t1 больше восьми секунд (если t1 > 8), то наше тело до восьми секунд двигалось без поворота. Чтобы сравнить t1 со значением 8, нужно просто найти это t1. Но как это сделать? Мы уже раньше говорили о том, что там где у параболы вершина, там скорость равна нулю. Действительно, тело, прежде чем повернуть в обратную сторону, должно на мгновение остановиться. Значит, при t = t1 должно быть v = 0. Иначе говоря, если в уравнение для скорости вместо t подставить t1, то вместо v мы одновременно должны подставить 0. Давайте сделаем это, тогда получим, что 0 = 2 - 0,4 t1. Отсюда находим время точки поворота t1 = 2/0,4 = 5 с. Очевидно, 5 < 8. Значит наше тело двигалось 5 секунд вдоль оси координат (значения координат увеличивались), а следующие 3 секунды оно двигалось обратно (значения координат уменьшаются). Это говорит нам о том, что в данной ситуации путь и перемещение не равны друг другу. Тело сначала удалилось, а потом вернулось немного обратно, значит переместилось не очень далеко, путь же, пройденный телом, будет увеличиваться постоянно, т.е. путь будет теперь больше перемещения (интересно, а может путь быть меньше перемещения?). Раз есть точка поворота, значит движение тела можно разбить на два участка: на первом участке координата увеличивалась, а на втором - уменьшалась. Весь путь, пройденный телом, складывается из путей, пройденных на каждом отдельном участке. Будем знать эти отдельные пути - сможем найти и общий (простым сложением).
Первый участок движения занял 5 секунд. В конце этого участка координата стала равна x = 2· 5 - 0,2· 52 = 5 м. Значит за первые 5 с тело прошло 5 м вдоль оси координат. За оставшиеся 3 с тело вернулось обратно, дойдя до конечной точки с координатой 3,2 м (которую мы уже сосчитали выше). Двигаясь против оси координат от точки 5 до точки 3,2, тело прошло путь 5 - 3,2 = 1,8 м. Следовательно, полный путь, пройденный телом, составляет 5 + 1,8 = 6,8 м.
В нашем случае у нас был еще один признак, говорящий о том, что у тела была точка поворота - это отрицательное значение скорости (-1,2 м/с). Знак “-” как раз и говорит о том, что скорость стала направлена в противоположном направлении (была 2, стала -1,2 - поменялся знак, поменялось направление). Однако, установив этот факт по знаку скорости, мы все равно в дальнейшем были бы вынуждены найти время точки поворота, разбить все движение на участки, найти путь на каждом участке и потом вычислить общий путь. То есть, мы все равно проделали бы все те же самые вычисления.
Задача № 27.
Условие.
Движение двух автомобилей по шоссе заданы уравнениями:
x1 = 2t + 0,2t2 и x2 = 80 - 4t.
Найти место и время встречи автомобилей. Найти расстояние между автомобилями через 5 с после начала отсчета времени. Найти координату первого автомобиля в тот момент, когда второй находился в начале координат.
Решение.
Какие ключевые признаки есть в условии, позволяющие нам проанализировать ситуацию? Признаки - “двух”, х1, х2, t2, t, “встречи”, “расстояние”, 5, “начало отсчета”, “координата”, “начало координат”. Видим, что признаков много, но не все из них важны для первоначального анализа, т.е. для определения характера движения тел.
Анализ признаков должен позволить отнести рассматриваемую ситуацию к какой-либо из известных нам моделей движения (на сегодняшний день мы с вами знаем только две таких модели: равномерное движение и равноускоренное движение).
То, что речь идет о двух телах, ясно из текста. Положение каждого из них определяется своей координатой. Обе координаты обозначены одной и той же буквой x, значит тела движутся вдоль одной прямой (вдоль оси координат х). Чтобы мы могли отличать координату первого тела от координаты второго, у них стоят номера 1 или 2. Итак, движение прямолинейное. В уравнении движения первого тела стоит квадрат времени (t2) - это явный признак равноускоренного движения. Значит первое тело движется прямолинейно и равноускоренно. В уравнении движения второго тела есть только время в первой степени (t) - это признак равномерного движения. Значит второе тело движется прямолинейно и равномерно. (К сожалению, у нас с вами нет времени сейчас углублять в такой интересный предмет как “Логика”, в котором рассматриваются важные для решения задач законы и правила. Там можно узнать о том, какие бывают определения, как правильно построить рассуждение, чем отличаются необходимые и достаточные условия или признаки и т.д.. Может быть когда-нибудь потом мы специально поговорим об этом, а сейчас давайте вернемся к решению задачи.)
Давайте получше поймем, что происходит с нашими телами (т.е. с автомобилями). Для этого нужно представить себе, где они были в начальный момент времени, как они движутся, где окажутся через несколько секунд.
Чтобы определить положение тел в начальный момент времени, нужно вычислить их координаты при t = 0. Подставим значение t = 0 в оба уравнения и получим: x10 = 0, x20 = 80. Значит, в начальный момент времени первое тело находилось в начале координат, а второе на расстоянии 80 м от него в сторону увеличения координаты. Для удобства направим ось координат вправо, тогда второе тело в начальный момент времени находилось в восьмидесяти метрах правее первого. Чтобы лучше представить дальнейшее движение тел, давайте найдем их скорости и исследуем их поведение (скорость имеет величину, которая может меняться или не меняться, увеличиваться или уменьшаться; и направление, которое может быть направлено влево или вправо и тоже может меняться или оставаться постоянной).
Для первого тела мы должны сравнить общие формулы равноускоренного движения и конкретные формулы движения нашего тела. Выпишем эти формулы рядом:
формулы для координаты:
x = x10 + v10 t + a1 t2 /2
x = 2t + 0,2 t2
формулы для скорости:
v1 = v10 + a1 t
v1 = ? + ? t.
В верхней строчке написаны общие формулы, а в нижней конкретные. Так как пока мы не знаем численных значений для начальной скорости и ускорения первого тела, то в конкретной формуле для скорости его движения на их местах стоят вопросительные знаки. Зато у нас есть возможность сравнить сразу формулы для координаты. Такое сравнение показывает, что при заменах x10 = 0, v10 = 2, а1/2 = 0,2 обе формулы станут абсолютно тождественными (неотличимыми). Это сразу позволяет нам сделать вывод, что начальная скорость первого тела v10 = 2 м/с, и его ускорение а1 = 0,4 м/с2. Теперь мы знаем, чем нужно заменить знаки вопросов в уравнении для скорости первого тела: заменяем и получаем v1 = 2 + 0,4t. В начальный момент времени его скорость была равна v1 = 2 + 0,4· 0 = 2 м/с. Это число положительное, значит скорость была направлена вдоль оси координат, т.е. в нашем случае вправо. В последующие моменты времени скорость продолжала оставаться положительной (т.е. все время направленной вправо) и увеличиваться по своему значению. Таким образом, первый автомобиль разгоняется из начала координат, двигаясь все время в правую сторону.
второй автомобиль движется равномерно. В общем случае, координата тела при равномерном движении меняется по закону x2 = x20 + v2 t. Для второго тела этот закон имеет следующий конкретный вид: x2 = 80 - 4t. Сравнение общей и конкретной формул показывает, что начальная координата второго автомобиля x20 = 80 м, а скорость его равномерного движения v2 = - 4 м/с (обратите внимание на знак!). Скорость имеет отрицательный знак, значит она направлена против оси координат. Если наша ось направлена вправо, значит скорость второго тела направлена влево. Таким образом, второй автомобиль движется влево из точки, расположенной на 80 м правее правого автомобиля. Они едут навстречу друг другу!
Если в начальный момент времени между машинами было расстояние 80 м, то через некоторое время это расстояние уменьшится (например, через 5 с). А еще через некоторое время эти автомобили встретятся (причем, место встречи будет где-то между началом координат и точкой с координатой 80). В реальной жизни эта встреча дорого бы обошлась обоим автомобилям, но в нашей задаче они спокойно прошли сквозь друг друга и как ни в чем ни бывало продолжили свое движение. Тогда еще через некоторое время второй автомобиль доедет до начала координат (где когда-то был автомобиль №1), а первая машина к этому времени уедет далеко вправо. Вот такое движение будут совершать тела в рассматриваемой задаче. Давайте нарисуем все это.
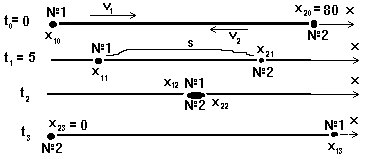
Из рисунка видно, что расстояние s между машинами в момент времени t1 = 5 с равно разности их координат: s = x21 - x11 = 80 - 4t1 - (2t1 + 0,2t12) = 80 - 4· 5 - 2· 5 - 0,2· 52 = 45 м.
Встреча - это момент совпадения координат. В момент встречи t2 координаты тел x12 и x22 совпали, т.е. стали равны: x22 = x12. Сами координаты находятся из уравнений для них, если в них подставить момент t2. Тогда для момента встречи имеем уравнение вида 80 - 4t2 = 2t2 + 0,2t22. Это выражение имеет одну букву - одну неизвестную величину t2, значит мы получили уравнение с одной неизвестной. Как решить это уравнение? Ничего не поделаешь, нужно вспоминать математику. Сначала перенесем все слагаемые в одну сторону: 0 = -80 + 4t2 + 2t2 + 0,2t22. Теперь приведем подобные (это второе и третье слагаемое): 0 = -80 + 6t2 + 0,2t22. Пытаемся по каким-либо признакам узнать тип этого уравнения (опять признаки, опять узнавание!). Главный признак уравнения - в какой наибольшей степени стоит неизвестная величина. Внимательно просматриваем с этой точки зрения все три слагаемых. Ага! Третье слагаемое стоит в квадрате, т.е. во второй степени (и степеней больше второй нет). Значит мы имеем дело с квадратным уравнением. Приводим уравнение к стандартному виду (a x2 + b x + c = 0; но в этой стандартной и привычной для математиков формуле буква х обозначает не координату какого-либо тела, а просто неизвестную величину), получаем: 0,2t22 + 6t2 -80 = 0. Теперь осталось вспомнить, как решается квадратное уравнение. Если память нас не подведет (или справочник, который конечно же у нас всегда под рукой), то мы вспомним, что квадратное уравнение вида a x2 + b x + c = 0 имеет два решения (говорят, два корня):
хпервое = (-b + Ц D)/(2a) хвторое = (-b + Ц D)/(2a).
Буквой D обозначается дискриминант, который находится как D = b2 - 4ac.
Чтобы найти решение уравнения для времени встречи нам нужно применить общее решение квадратного уравнения к нашему конкретному уравнению. Для этого напишем общие и конкретные выражения рядом и сравним их (такую процедуру мы уже проделывали не раз). Итак:
a x2 + b x + c = 0 D = b2 - 4ac
0,2t22 + 6t2 -80 = 0 D = ?2 - 4??
хпервое = (-b + Ц D)/(2a) хвторое = (-b + Ц D)/(2a)
tпервое = (-? + Ц D)/(2?) tвторое = (-? + Ц D)/(2?).
В первой строчке записаны выражения общего вида, а во второй конкретного, причем там, где мы не знаем конкретных значений, стоят вопросительные знаки. Однако, мы легко заменим эти знаки числами, если внимательно посмотри на первую пару уравнений (которые записаны в первом столбике). Нижнее уравнение - это конкретный частный случай верхнего. Верхнее уравнение в точности переходит в нижнее, если принять (попробуйте тут остановиться, написать сначала самостоятельно значения для a, b и c, а потом проверьте себя).
У меня получилось, что а = 0,2, b = 6 и с = -80. Теперь мы легко вычислим дискриминант D = 62 - 4· 0,2· (-80) = 100. Зная дискриминант, находим оба корня уравнения:
tпервое = (-6 + Ц 100)/(2· 0,2) = 10, tвторое = (-6 - Ц 100)/(2· 0,2) = - 40.
Итак, мы получили два решения, т.е. у автомобилей было два времени встречи. Если бы мы были математиками, мы бы на этом остановились. Но так как мы с вами физик, то мы знаем, что встреча у наших автомобилей могла произойти только один раз! После того как они встретились и разъехались снова, они продолжали удаляться друг от друга и встретиться более не могли. Вывод, из двух найденных нами моментов времени встречи на самом деле правильным является только один. Какой же, встает вопрос? Чтоб на него ответить, нужно понять физический смысл полученных решений. Первое время встречи не вызывает у нас никаких отрицательных эмоций. Действительно, вполне вероятно, что автомобили встретились через 10 с после начала отсчета времени (раз они ехали навстречу друг другу). Но вот второй момент времени выглядит подозрительно. Время -40 с означает, что это было за 40 секунд до начала отсчета времени. Однако, в этот момент времени тела должны были находиться еще дальше друг от друга, чем даже t = 0! Кроме того, по условию задачи нас вообще не интересует, что было ДО начала отсчета. Так что tвторое в нашем случае не имеет физического смысла и должно быть отброшено. Таким образом, время встречи автомобилей равно 10 с. Место встречи определяется общей координатой автомобилей, которую мы можем найти из любого уравнения. Мы возьмем уравнение движения второго автомобиля, так как оно проще (квадрат не надо вычислять). Тогда координата встречи будет x22 = 80 - 4tпервое = 80 - 4· 10 = 40 м.
Осталось определить координату первого тела в тот момент, когда второй находился в начале координат. Иначе говоря (смотрите на рисунок) нас интересует координата х13 в момент времени t3 когда было x23 = 0. Чтобы найти координату х13 нам нужно знать время t3. Но чтобы найти это время мы должны воспользоваться какой-то информацией (это всегда так, либо мы знаем ответ сразу, либо ищем его с помощью дополнительной информации, которую должны откуда-то извлечь). Информация всегда отвечает на какие-то вопросы. Нас интересует момент t3. Значит, спросим себя, а что мы знаем про момент t3? Если мы еще раз перечитаем условие, то обнаружим лишь то, что в этот момент времени второй автомобиль находился в начале координат. Значит, для определение момента времени t3 у нас имеется только одно условие x23 = 0. Смысл этого условия прост: если в уравнение для координаты второго тела подставить время t3, то координата будет равна нулю. Превратим эти слова в действия, подставим в уравнение для координаты второго тела ноль вместо х2 и t3 вместо t. Получим: 0 = 80 - 4 t3. Это уравнение на момент времени t3, которое легко решается. Из него мы находим t3 = 20 с.
Еще одно последнее усилие, и решение закончено мое.
Все что нам осталось сделать - подставить время t3 = 20 c в уравнение для координаты первого тела и сосчитать, что же получится. Результат будет следующий: x13 = 2t3 + 0,2t32 = 2· 20 +0,2· 202 = 120 м.
Небольшое введение для тех, кто только приступает к изучению физики
Список основных определений физических понятий по разделу “Кинематика”
Схема взаимосвязи основных физических величин по разделу “Кинематика”
Задачи на понятия “путь” и “перемещение”
Задачи на прямолинейное равномерное движение
Задачи на закон сложения скоростей
Задачи на прямолинейное равноускоренное движение
Задачи на прямолинейное равноускоренное движение (продолжение 1)
Задачи на прямолинейное равноускоренное движение (продолжение 2)