Задачи по кинематике.
Задача №1.
Условие.

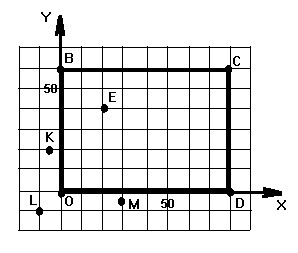
На рисунке изображен план футбольного поля.
Найдите координаты угловых флажков (O,B,C,D), мяча (E), зрителей (K,L,M).
Решение.
Прочитав условие, выделяем основные понятия, в которых содержится весь смысл задачи. Понятия для нас с вами - это главные слова в тексте. В этой задаче их всего шесть: план, поле, координаты, флажок, мяч, зритель. Теперь мы легко ответим на первый вопрос: "С чем, т.е. с какими конкретными телами, вещами (по научному - с объектами), мы имеем дело в этой ситуации. Мы имеем дело с полем, флажками, мячом и зрителями.
Все тала отличаются друг от друга. То, чем они отличаются, называется признаками. Этих признаков огромное множество: цвет, форма, масса, температура, расположение, скорость, ускорение и многое, многое другое. Мы должны знать по крайней мере некоторые признаки у тех тел, с которыми имеем дело в нашей задаче. Что мы можем сказать, например, про флажок D? Он есть, расположен в одном из углов поля, покоится, возможно развивается на ветру, наверное, имеет красный цвет и у него есть координаты. То что у него есть координаты нам известно хотя бы из условия (там так и написано: найти координаты флажков - но ведь нельзя было бы найти то, чего нет!). Среди этих признаков есть СУЩЕСТВЕННЫЕ для нашей ситуации (т.е. важные) и не существенные (т.е. не важные). Нам не важно, какого цвета будет стоять флажок в этом углу, красный или зеленый - какого бы цвета флажок там не стоял, у них у всех будут одинаковые координаты (ведь место-то одно и то же, а координаты - это характеристики МЕСТА, а не флажка). Поэтому из всех известных нам признаков мы должны выбрать только существенные, а про несущественные просто забыть. Конечно, в сложных задачах мы можем сделать ошибку и отбросить какой-либо существенный признак, или оставить не существенный, но в том то и состоит искусство решения задач, чтобы точно определить, что важно, а что нет, а в случае ошибки, исправить ее.
Единственный существенный признак в этой задаче - координаты. Если мы это себе сказали, то пришла пора вспомнить поподробнее, что же такое "координата". Итак, координаты - это числовые характеристики, однозначно задающие положение материальной точки в пространстве. Заодно придется вспомнить, что материальная точка - это тело, размерами которого в рассматриваемых условиях можно пренебречь, т.е. его размеры для решения задачи не важны. Положение - это место, в котором находится наше тело. Нам безразлично, какое тело находится в этом месте, у всех у них будут одни и те же координаты (если одно тело убрать и на его место поместить другое). В нашей задаче размеры мяча, флажков и даже зрителей роли не играют, так как их места обозначены на плане поля точками. Найти координаты наших тел - это значит найти координаты точек, в которых они находятся.
Координаты бывают разные. Но в школьном курсе физики изучаются только декартовы координаты (по имени ученого, который их изобрел). Вспомним, что такое декартовы координаты. Декартовыми координатами называются числа, которые находятся таким способом:
Рисуются две прямые под прямым углом (90о) друг к другу, т.е. взаимно перпендикулярно.
На каждой прямой выбирается положительное направление, точка пересечения принимается за нулевое значение (начало отсчета), и на каждой прямой задается единичный интервал, с помощью которого затем можно отсчитать все остальные числа. Получим две взаимно перпендикулярных числовых оси. Такая система и называется декартовой системой координат. Одна из осей обозначается обычно буквой x, другая буквой y.
Из точки, координаты которой мы ищем, нужно аккуратно опустить перпендикуляра на каждую из осей. Эти перпендикуляры попадут в какие-то значения чисел. Вот эти-то числа и называются декартовыми координатами точки, а сокращенно, просто координатами.
В нашей задаче почти вся работа уже проделана: оси нарисованы, стрелки выбраны, буквы расставлены. Осталось определить численные значения стороны одной клеточки, а затем найти и сами координаты. Давайте взглянем на рисунок. Нам надо найти значение стороны клеточки, т.е. число. Внимательно смотрим, нет ли на рисунке каких-нибудь чисел. Есть! рядом с пятой по счету клеточкой (от начала координат) написано число 50 (и по оси x, и по оси y). Если на пять клеточек приходится 50 единиц, то на одну в пять раз меньше, т.е. 10. Итак, цена деления нарисованных осей-линеек равна десяти единицам. Начинаем искать координаты.
Точка O находится в начале координат, где нами самими при построении осей назначается число ноль и для оси x, и для оси y. Значит у точки O координаты x = 0, y = 0. В сокращенном виде это записывают следующим образом O(0,0) (на первом месте в скобках стоит значение x, на втором месте стоит значение y). Берем точку B. Она находится на оси y. Перпендикуляр к оси y, проходящий через точку B, отсекает на оси y число, соответствующее значению шестой клеточки. Так значение одной клеточки равно 10 единиц, то значение шестой клеточки будет равно 60 единиц (6 раз по 10). Значит координата y у точки B равна 60. Если же из этой точки опускать перпендикуляр на ось x, то попадем в начало координат, т.е. в значение ноль. Значит координата x у точки B равна нулю. Можем записать ответ B(0,60). Видите, все очень просто! Нужно только опустить перпендикуляры и посмотреть на какую ось они упали и какое число они отсекли!
Теперь легко найти координаты остальных точек. Перпендикуляры из точки C попадают на оси, отсекая число 80 (8 клеточек по 10 единиц каждая) на оси x, и число 60 на оси y, значит для точки С x = 80, y = 60, т.е. пишем С(80,60). Точка D лежит на том же перпендикуляре к оси x, что и точка С, т.е. у нее тоже x = 80. Перпендикуляр на ось y из точки D попадает в ноль, т.е. y = 0 и мы пишем D(80,0). Перпендикуляры на оси из точки E дают значения x = 20 (на оси x отсекаются две клетки по 10 единиц каждая) и y = 40, т.е. ответ E(20,40). Перпендикуляр из точки L на ось x попадает левее ноля. Это означает, что он попадает в отрицательное число, так как мы знаем, что положительные числа идут от ноля по стрелке, т.е. для оси x вправо. Тогда влево от ноля идут отрицательные. Так как отсекается при этом одна клеточка, то значение координаты должно быть "минус одна клеточка", то есть -10! Итак, для точки L x = -10. Точно так же, опуская из точки L перпендикуляр на ось y получаем y = -10. Пишем ответ для точки L: L(-10,-10).
Теперь с последними двумя точками расправимся мгновенно. Перпендикуляр на ось y из точки K отсекает две клетки, y = 20. Перпендикуляр на ось x из точки K отсекает половину клетки слева от ноля. Значит для точки K x = "минус половина клетки" = -10/2 = -5. Пишем K(-5,20). Для точки M имеем M(30,-5). Обязательно проверьте сами этот результат, а если нужна помощь - напишите мне.
Отметим, что для решения этой задачи необходимо знать и понимать два физических понятия: координаты и декартова система координат - которые в списке основных понятий имеют номер 10 и номер 11. Если посмотреть решение и сравнить его с определениями, данными в списке, то увидим полное совпадение. В принципе, все решение могло бы состоять из одного предложения: " В соответствии с пунктом 10 и пунктом 11 списка основных понятий" имеем O(0,0), B(0,60), C(80,60), D(80,0), E(20,40), L(-10,-10), K(-5,20) и M(30,-5)."
Задача №2.
Условие.
Резиновый мячик бросили с высоты 3 м. Он отскочил от пола и был пойман на высоте 4 м. Найти путь и перемещение мяча.
Решение.
С чем имеем дело? В этой задаче мы имеем дело с мячом и полом. Что происходит? Мяч движется, причем характер движения нам известен из нашего опыта: очевидно, что мячик бросили вниз с силой, так что при отскоке он подлетел выше того места, с которого он начал свободно сам по себе падать. Нечего думать - нужно рисовать. Мяч из точки А упал в точку В и, отскочив от пола, поднялся затем в точку С.
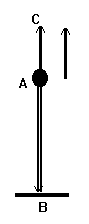
Главное тело задачи - очевидно мяч. Параметры, которыми он может описываться - размер, цвет, температура, цена, материал изготовления и т.п.. Важны ли нам в этой задаче перечисленные параметры? Это зависит от того, что мы хотим найти. Если бы нас спросили, является ли этот мяч футбольным или теннисным, тогда нам были бы важны размеры и материал. А нас спрашивают, каковы путь и перемещение. Эти понятия связаны с движением мяча, т.е. с изменением его положения в пространстве с течением времени (см. пункт 3 "Списка"). Цвет и пр. в этом случае для нас не существенны. А что существенно? Чтобы ответить на этот вопрос, необходимо вспомнить, что такое "путь" и что такое "перемещение" (ведь их нужно искать, а как бы мы искали то, что не знаем как это выглядит). Смотрим в наш список основных понятий. Под пунктом 7 находим, что путь - это длина траектории. Раз встретилось новое понятие, то сразу смотрим и его; траектория - это (см. пункт 6) линия, по которой движется материальная точка. В нашем случае размеры мяча не существенны, так что мы считаем его точкой. Линия его движения - это линия, нарисованная сначала из А в В, а затем продолженная из В в С. Это и есть траектория мяча. Чтобы найти путь (читаем дальше пункт 7) нужно проложить ниточку вдоль траектории, затем растянуть ее вдоль линейки и найти ее длину. Если мы это делаем, то получаем, что наша ниточка будет состоять из двух отрезков: отрезка АВ и отрезка ВС. Тогда ее длина будет состоять из двух длин, или точнее из длин двух отрезков: из длины отрезка АВ и длины отрезка ВС. Получаем, что ПУТЬ = АВ + ВС. По условию, расстояние АВ = 3 м, а расстояние ВС = 4 м, так что весь путь равен 3 + 4 = 7 м. Обычно путь обозначают буквой S, так что можем записать: S = 7 метров. Теперь ищем перемещение. Как мы уже начали привыкать, смотрим в список, что же это такое. В пункте 8 читаем, что перемещение - это вектор, соединяющий начальное и конечное положение тела. А в пункте 9 нам напоминают, что вектор - это стрелка. У нашего тела (мяча, имеется в виду) начальной точкой является точка А, а конечной - точка С. Значит наш вектор перемещения начинается в точке А и заканчивается в точке С (на рисунке эта стрелка нарисована отдельно, несколько правее траектории, чтобы лучше было ее видно). Слова "найти перемещение" означаю "найти длину вектора перемещения", то есть найти длину этой стрелки. Из чертежа видно, что отрезок ВС состоит как раз из отрезков АВ и АС, т.е. ВС = АВ + АС. Но длина отрезка АС и есть длина вектора перемещения. Значит, чтобы найти перемещение, надо найти АС, что легко сделать, так как теперь мы видим, что АС = ВС - АВ = 4 - 3 = 1 м. Перемещение обозначают обычно через DS, так что получаем DS = 1 м.
Задача №3.
Условие.
Вертолет, пролетев в горизонтальном направлении по прямой 40 км, повернул под углом 90о и пролетел еще 30 км. Найти путь и перемещение вертолета.
Решение.
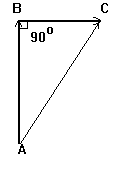
Задача по смыслу совсем как предыдущая: какое-то тело как-то двигалось, найти путь и перемещение. Раз смысл задачи такой же, значит и ход решения такой же. Все понятия нам уже известны, так что рисуем чертеж и сразу ищем все что нужно.
Мы имеем дело с телом, которое движется сначала в одном направлении, затем в другом. Вертолет (для нас материальная точка) из точки А летит по прямой до точки В 40 км, в точке В поворачивает под прямым углом (90о), затем движется снова по прямой до точки С 30 км. (Откуда мы все это знаем? Да из условия!). Именно так мы и нарисуем наш чертеж, или начертим наш рисунок.
Путь - длина траектории, а траектория состоит из двух отрезков: АВ и ВС. Тогда S = АВ + ВС = 40 + 30 = 70 км. Путь найден. Перемещение - это стрелка, соединяющая начальную точку А с конечной точкой С. Найти перемещение - значит найти длину этой стрелки. Понятно, что эта длина должна быть связана с длинами отрезков АВ и ВС, должна выражаться через них. (Понятно ли, почему понятно? Ведь если мы укоротим или удлиним АВ, то изменится и АС! Тоже самое справедливо и для ВС. Это и означает, что АС зависит от АВ и ВС). Раз эти величины связаны, то надо поискать, что же их связывает. А в нашей задаче отрезки АВ, ВС и АС связывает только чертеж! Ничего не поделаешь, внимательно смотрим на чертеж. Что мы видим? Мы видим и узнаем геометрическую фигуру - это треугольник (мы все знаем, что такое треугольник, не правда ли?). Причем, треугольник не простой, а прямоугольный, так как в нем есть прямой угол. Что мы знаем про прямоугольные треугольники? В них есть катеты и гипотенуза, у них есть углы, для них справедливы разные формулы: теорема Пифагора, формулы для синусов, косинусов и тангенсов. Может ли что-нибудь из всего того, что мы знаем про прямоугольные треугольники, нам пригодиться сейчас? Думаем, что нам надо найти - длину отрезка АС через длины отрезков АВ и ВС. Иначе говоря, нам надо найти длину гипотенузы через длины катетов. Для этого есть теорема Пифагора! (Вот что значит хорошая память!) По теореме Пифагора АВ2 + ВС2 = АС2 . Тогда АС2 = 402 + 302 = 2500 и DS = АС = O 2500 = 50 км. Конец.
Небольшое введение для тех, кто только приступает к изучению физики
Список основных определений физических понятий по разделу “Кинематика”
Схема взаимосвязи основных физических величин по разделу “Кинематика”
Задачи на прямолинейное равномерное движение
Задачи на закон сложения скоростей
Задачи на прямолинейное равноускоренное движение
Задачи на прямолинейное равноускоренное движение (продолжение 1)
Задачи на прямолинейное равноускоренное движение (продолжение 2)
Задачи на прямолинейное равноускоренное движение (окончание)
Задачи на вертикальное падение
Задачи на вертикальное падение (окончание)
P.S. Методика организации уроков и примеры используемых дидактических материалов излагаются в файле Методика и дидактика занятий по обучению учащихся искусству решения задач по физике