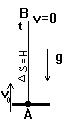
Задача №33.
Условие.
Камень бросили вертикально вверх со скоростью 10 м/с. На какую высоту поднимется камень?
Решение.
По всем известным нам уже признакам, мы имеем дело с прямолинейным равноускоренным движением, которое происходит с ускорением свободного падения g = 10м/с2. Этими признаками являются слова “бросили” (значит ПАДАЕТ) и “вертикально” (значит по прямой).
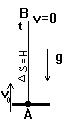
Прямолинейное равноускоренное движение описывается двумя формулами v = v0 + at; D s = v0 t + at2/2.
Очень важно разобраться со всеми ключевыми понятиями задачи, которые явно или не явно присутствуют в ее условии. “Бросили со скоростью” означает, что начальная скорость равна v0 = 10 м/с. “Поднимется на высоту” означает, что долетит до верхней точки, где остановится (на какое-то мгновение, прежде чем начать падать обратно вниз, но нас это сейчас не интересует). “Верхняя точка” означает точку, в которой тело останавливается, т.е. в которой скорость тела становится равна нулю: v = 0. “Высота” означает здесь перемещение тела от нижней точки до верхней: Н = АВ = Ds.
Теперь нужно определить, есть ли у нас векторные величины? Есть: это начальная скорость, перемещение и ускорение. Раз есть векторные величины, нужно выбрать направление положительных значений. Направим ось вверх. Тогда начальная скорость и перемещение будут направлены вдоль оси, а ускорение против. Значит, ускорение нужно брать со знаком “-”: а = - g = - 10 м/с2.
Теперь можно делать подстановку. Однако для разнообразия, не будем пока подставлять числа (кроме нолей), а используем буквенные обозначения. Тогда получаем:
0 = v0 - gt; H = v0 t - g t2 /2.
Выражаем из первой формулы время: t = v0 /g, и подставляем его во вторую формулу. Получим, H = v0 t - g t2 /2 = v0· v0/g - g(v0 /g)2/2 = v02/(2g). Эту формулу стоит запомнить. Мы доказали, что если тело бросить вертикально вверх с начальной скоростью v0, то он поднимется на высоту H = v02/(2g), если не учитывать сопротивление воздуха.
Теперь подставим числа и найдем искомую высоту: H = v02/(2g) = (10)2/(2· 10) = 5 м.
Задача № 34.
Условие.
Во сколько раз нужно увеличить начальную скорость брошенного вверх тела, чтобы его высота подъема увеличилась в 4 раза?
Решение.
Мы опять имеем дело с телом, которое бросили вертикально вверх. Только что в предыдущей задаче мы доказали, что высота подъема Н такого тела находится по формуле H = v02/(2g), где v0 - начальная скорость и g - ускорение свободного падения (влияние воздуха не учитывается).
Самое главное, это понять, что в этой задаче мы ДВА раза бросаем тело вверх. Сначала мы бросаем на одну высоту, а потом на другую. Следовательно, у нас имеется ДВЕ высоты подъема Н1 и Н2 и ДВЕ начальных скорости v10 и v20 (иначе бы высоты не различались). А это значит, что мы должны ДВА раза написать формулу для высоты:
H1 = v102/(2g); H2 = v202/(2g).
По условию задачи, Н2 = 4· Н1. Найти же нужно v20/v10. Эта проблема теперь является чисто математической. Выражаем из написанных формул начальные скорости и ищем их отношение: v20/v10 = Ц (2gH2)/Ц (2gH1) = Ц (H2/H1) = Ц 4 = 2. Ответ, чтобы высота подъема увеличилась в четыре раза, скорость нужно увеличить в два раза.
Задача № 35.
Условие.
Тело брошено вертикально вверх со скоростью 30 м/с. На какой высоте, и через сколько времени скорость тела станет по модулю в три раза меньше?
Решение.
Мы уже хорошо себе представляем, что если тело бросить вертикально вверх, то оно будет совершать прямолинейное равноускоренное движение с ускорением g. При этом скорость тела будет сначала постепенно убывать до нуля, в верхней точке траектории тело на мгновение остановится и начнет падать вниз, постепенно разгоняясь. Если начальная скорость равна 30 м/с, а скорость в верхней точке равна нулю, то где-то между ними есть точка, в которой скорость равна одной трети от начальной, т.е. 30/3 = 10 м/с. Причем, эта скорость будет наблюдаться два раза: один раз, когда тело летит верх, и его скорость уменьшается от 30 до 10 м/с (а потом до нуля); второй раз, когда тело падает обратно вниз, и его скорость увеличивается от 0 до 10 м/с (а потом снова до 30).
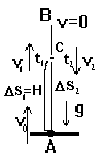
Итак, начиная движение из точки А со скоростью v0 = 30, тело движется вверх, и, пройдя перемещение D S1 = АС = H за время t1, уменьшает свою скорость в три раза, т.е. до значения v1 = 10. Скорости v0 и v1, и их значения мы написали со знаком “+”. Это означает, что значения векторов, направленных вниз, мы будем писать со знаком “-” (например, ускорение а = -g).
После момента времени t1 тело еще несколько секунд двигалось вверх до остановки, потом начало падать и к моменту времени t2 снова приобрело скорость 10 м/c, только направленную вниз. Значит, в момент времени t2 скорость v2 = -10. Перемещение, сделанное телом за время t2, обозначим D S2.
Из общих формул прямолинейного равноускоренного движения для обоих конкретных моментов времени t1 и t2 мы можем записать:
v1 = v0 - gt1; D S1 = v0 t1 - g t12 /2;
v2 = v0 - gt2; D S2 = v0 t2 - g t22 /2.
Подставляем численные данные:
10 = 30 - 10· t1; D S1 = 30 · t1 - 10· t12 /2;
- 10 = 30 - 10· t2; D S2 = 30· t2 - 10· t22 /2.
Теперь легко найти сначала времена t1 и t2, а затем перемещения D S1 и D S2.
Вычисляем: t1 = 2 c, t2 = 4 c, D S1 = H = D S2 = 40 м.
Задача № 36.
Условие.
Пловец, спрыгнув с пятиметровой вышки, погрузился в воду на глубину 2 м. Сколько времени и с каким ускорением он двигался в воде?
Решение.
Телом в этой задаче является пловец. Вряд ли его можно считать в таких условиях материальной точкой. И сам процесс прыжка: разбег, толчок, полет - не слишком похож на свободной падение. Однако в предложенных нам условиях у нас нет другого способа решить задачу. Мы должные сложный реальный процесс прыжка и погружения пловца в воду заменить простой моделью - свободным падением материальной точки, которая, попав в воду, постепенно останавливается. Каму-то эта модель может показаться слишком грубой. Но в жизни, в технике, в науке, модель (даже на вид самая грубая) может считаться вполне удовлетворительной, если ее расчетные данные укладываются в погрешности, которые нас удовлетворяют.
Итак, анализируем предложенную нам физическую ситуацию, исходя из самых простых представлений, и одновременно рисуем чертеж.
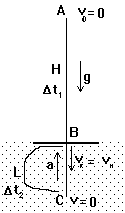
В данной ситуации имеется два участка движения: первый участок движения проходит в воздухе, второй - в воде.
Из точки А без начальной скорости начало падать тело. Не учитывая сопротивление воздуха, можно сказать, что движение тела буде прямолинейным и равноускоренным с ускорением g, которое направлено вниз к воде. За промежуток времени D t1 тело совершит перемещение DS1 = АВ = Н - высоте, с которой падало тело. На этом участке движения тело приобретет скорость vк - конечную скорость движения на первом участке.
Второй участок движения начинается в точке В. В этой точке тело имело скорость vк. Значит, эта же самая скорость (конечная скорость первого участка) является начальной скоростью для второго: vк = vн. Перемещение, совершаемое телом на втором участке движения D S2 = ВС = L, происходит за промежуток времени D t2. За это время тело постепенно останавливается, снижая скорость до нуля. Конечная скорость на втором участке v = 0. Раз скорость уменьшается, следовательно, ускорение препятствует ее увеличению, т.е. ускорение направлено против скорости. Если у нас скорость направлена вниз, то тогда ускорение движения на втором участке направлено вверх. Причем, его численное значение никак не может совпадать со значением ускорения свободного падения, ведь на тело теперь действует вода. Именно она заставляет тело останавливаться (а потом всплывать).
На обоих участках движение прямолинейное и равноускоренное. На первом участке происходит ПАДЕНИЕ, а на втором участке нужно найти ускорение, что говорит о том, что оно не меняется.
Тогда, мы должны два раза - для каждого участка по отдельности - написать формулы равноускоренного движения. Пишем.
Для первого участка движения:
vк = 0 + g· D t1; H = g· D t12/2.
Для второго участка движения:
0 = vн - a· D t2; L = vн· D t2 - a· D t22/2.
Остальное - дело техники. Осталось подставить все известные нам численные значения и решить полученную систему уравнений. Давайте проделаем все это и получим ответ. Напомню, что у нас по условию Н = 5 м, g = 10 м/с2, L = 2 м. Имеем:
5 = 10· D t12/2 Ю (этот значок заменяет слово “следовательно”) D t12 = 1 Ю D t1 = 1 с Ю vк = 10· 1 = 10 м/с Ю vн = vк = 10 м/с.
Используя уравнения движения на первом участке, мы определили значение скорости, которая является начальной для движения на втором участке. Теперь нужно рассмотреть остальные два уравнения. Подставим числа в них.
0 = 10 - a· D t2; 2 = 10· D t2 - a· D t22/2.
Это два уравнения с двумя неизвестными. Такая система решается стандартным методом: из простого уравнения выражается одна неизвестная и подставляется в сложное, которое после этого превращается в формулу с одной буквой.
Выразим D t2.
D t2 = 10/а Ю 2 = 10· (10/а) - а· (10/а)2/2 Ю 2 = 100/а - 50/а Ю 2 = 50/а Ю а = 25 м/с2.
Тогда осталось найти время D t2 = 10/а = 10/25 = 0,4 с.
Задача № 37.
Условие.
Тело свободно падает с высоты 80 м. Каково его перемещение в последнюю секунду падения?
Решение.
Свободное падение - это прямолинейное равноускоренное движение с ускорением g = 10 м/с2.
В нашей задаче самое главное понять, что такое “последняя секунда”.
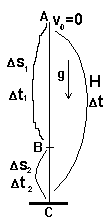
С высоты Н = АС = 80 м подает тело. Через время D t оно упало на землю в точку С. За секунду до этого оно находилось еще над поверхностью земли в точке В. Движение от точки В до точки С и заняло по условию задачи одну секунду. Значит, D t2 = 1 с, а найти нужно D s2 = ВС. Точка В делит все перемещение тела на два участка АВ и ВС. На КАЖДОМ из них, так же как и на всем участке движения, происходит это прямолинейное равноускоренное движение с ускорением g = 10 м/с2. Значит, для каждого участка, так же как и для всего перемещения, мы можем записать формулы прямолинейного равноускоренного движения.
В условии ничего не говориться о скоростях, поэтому попытаемся обойтись только формулами для перемещений. Если понадобится, мы всегда сможем выписать и формулы для скоростей.
Для полного перемещения имеем H = g· D t2/2.
Для участка АВ запишем D s1 = g· D t12/2.
Мы также сразу можем записать, что полное время движения складывается из времени движения на каждом участке D t = D t1 + D t2, а полное перемещение - из перемещений участков H = D s1 + D s2. В четырех записанных формулах есть четыре неизвестные величины: D t, D t1, D s1, D s2. Четыре уравнения с четырьмя неизвестными должны решаться, значит, нам действительно не понадобятся формулы для скоростей. Итак:
H = g· D t2/2; D s1 = g· D t12/2; D t = D t1 + D t2; H = D s1 + D s2.
Подставим все численные данные, какие мы только знаем:
80 = 10· D t2/2; D s1 = 10· D t12/2; D t = D t1 + 1; 80 = D s1 + D s2.
Теперь видно, что из первой формулы мы найдем полное время движения, затем из третьей формулы найдем время движения на первом участке, потом из второй формулы найдем перемещение АВ, и, наконец, из четвертой формулы найдем искомую величину.
Вперед, за вычисления: D t = 4 c, D t1 = 3 c, D s1 =45 м, D s2 = 35 м.
Задача № 38.
Условие.
Сколько времени падало тело, если за последние две секунды оно прошло 60 метров?
Решение.
Какие вопросы требуют нашего ответа при анализе задачи?
С чем (с какими объектами) мы имеем дело, сколько в задаче тел, что представляет собой каждый объект, каковы его свойства, что происходит с телами, сколько важных моментов времени нужно учесть, сколько участков движения надо рассмотреть, каков характер движения на каждом участке, по каким признакам определить характер движения, каковы эти признаки в нашей задаче, какова общая физическая модель которой соответствует данная конкретная ситуация, какие физические величины важны в этой модели и какими формулами они взаимосвязаны?
У нас уже накоплен достаточно большой опыт, чтобы понять следующее: мы имеем дело с перемещением тела в пространстве с течением времени, т.е. с механическим движением; тогда нас интересует в первую очередь форма траектории и характер поведения скорости, так как это для нас основные признаки ситуации; в условии задачи, в свою очередь, есть частные признаки в виде слов “падало”, “тело”, “последние две секунды”, а кроме них подразумевается признак “свободно”; эти частные признаки говорят нам о том, что движение прямолинейное и равноускоренное, с ускорением свободного падения, что есть три важных момента времени (начальный, конечный и за две секунды до конечного); значит, есть два участка движения (не считая полного участка); общая модель для данной задачи - прямолинейное равноускоренное движение; основные физические величины для такой модели - перемещение, интервал движения, скорость и ускорение; связаны эти величины двумя стандартными формулами v = v0 + a· D t, D s = v0· D t + a· D t2/2.

Рисуем чертеж. Внешне он не отличается от чертежа предыдущей задачи: из точки А без начальной скорости падает тело, за какое-то время долетает до точки В и потом еще 2 секунды движется до земли, успев пройти за это время 60 м. Мы можем использовать в этом случае все те же самый обозначения и записать те же формулы:
H = g· D t2/2; D s1 = g· D t12/2; D t = D t1 + D t2; H = D s1 + D s2.
Напомню, что прежде чем выписывать формулы, нужно также ответить на ряд вопросов: какие основные физические величины есть в задаче, как они обозначены (обязательно разные - по разному), есть ли векторные величины, куда они направлены, куда выбрано положительное направление, есть ли в условии дополнительные сведения о связи величин, можно ли из описания ситуации определить дополнительные связи между величинами, для каждого ли тела и важного момента времени или участка движения записаны основные формулы, правильно ли осуществлена замена общих величин на конкретные величины данной задачи?
Итак, мы выписали основные формулы. Они не отличаются от формул предыдущей задачи, но теперь у нас иные численные данные. Подставим их в формулы:
H = 10· D t2/2; D s1 = 10· D t12/2; D t = D t1 + 2; H = D s1 + 60.
С точки зрения математики, мы опять имеем четыре уравнения с четырьмя неизвестными (H, D t, D s1, D t1). Однако пока у нас нет формулы с одной буквой. Следовательно, наша первая цель, сконструировать из этих уравнений одну формулу с одной буквой. Для этого есть единственный способ: из одних формул выражать одни неизвестные и подставлять в другие формулы, пытаясь делать и так и эдак, пока не получится то, что нужно. Собственно говоря, это называется действовать методом проб и ошибок, но это единственный универсальный метод, известный на сегодня в науке. Поскольку у меня имеется большой опыт таких проб и ошибок, то я знаю заранее, что выражать, откуда выражать и куда подставлять (следите за стрелкам).
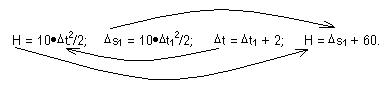
Проделав указанные подстановки, мы из четвертой формулы получим уравнение:
10· (D t1 + 2)2/2 = 10· D t12/2 + 60.
В этом уравнении теперь только одна неизвестная величина - D t1. Раскрываем скобки и находим это время: 10· D t12/2 + 10· 2· D t1· 2/2 + 10· 22/2 = 10· D t12/2 + 60 Ю 20· D t1 + 20 = 60 Ю 20· D t1 = 40 Ю D t1 = 2 с. Теперь легко находим D t = 2 + 2 = 4 с. Заодно можно найти и с какой высоты тело падало: Н = 10· 42/2 = 80 м. Кроме того, можно теперь найти и перемещение на первом участке, и скорость в момент падания, и скорость в точке В - так что если нам встретится задача с таким же условием, но с другими вопросами, то мы будем делать все то же самое, только чуть дольше.
Задача № 39.
Условие.
С балкона, находящегося на высоте 25 м над поверхностью земли, бросили вертикально вверх мячик со скоростью 20 м/с. Написать формулы зависимости скорости и координаты мячика от времени, выбрав за начало отсчета а) точку бросания; б) поверхность земли. Найти, через сколько времени мячик упадет на землю. С какой скоростью он упадет? Какой путь и перемещение он проделал за время полета?
Решение.
Начнем сразу с чертежа. С балкона из точки А с начальной скоростью v0 = 20 м/c
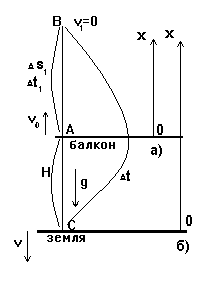
вверх бросили тело. Земля притягивает мячик к себе вниз, и он постепенно останавливается. В точке В его скорость стала равна нулю v1 = 0. В это же мгновение мячик начинает двигаться вниз к земле и, в конце концов, падает на нее в точку С со скоростью v. Движение, как мы уже хорошо знаем, является прямолинейным и равноускоренным с ускорением g = 10 м/с2.
Будем искать неизвестные величины. Что мы для этого знаем?
За все время полета D t тело совершило перемещение D s, которое идет из точки А в точку С (из начальной в конечную). Расстояние АС = Н = 25 м. Положительное направление мы выбрали сразу вверх (для обеих осей х). Перемещение же направлено вниз. Следовательно, D s = - 25. Ускорение также направлено вниз (а = - 10), но начальная скорость направлена вверх (v0 = 20). Тогда, по общей формуле для перемещения при прямолинейном равноускоренном движении, для полного полета мяча можно записать: - 25 = 20· D t - 10· D t2/2.
Это квадратное уравнение для неизвестного времени всего полета D t. Сначала нужно записать его в стандартном виде, потом найти дискриминант, потом вычислить два корня и оставить из них положительный (так как время должно быть больше нуля) или наименьший (так как тело падает на землю только один раз). Один раз подобные вычисления мы уже проделывали. В этот же раз сделайте самостоятельно это полезное упражнение. Ответ получится D t = 5 с. Раз время полета известно, ускорение известно, сразу можно найти конечную скорость: v = 20 - 10· 5 = - 80 м/с. Знак “-” говорит о том, что конечная скорость направлена против оси, т.е. вниз. Именно так и есть на самом деле.
Полное перемещение мяча мы уже знаем, осталось только найти путь и написать уравнения для координат.
Значит, надо вспомнить, что такое путь. Путь - это длина траектории. Траектория - это линия по которой движется тело. В нашем случае траектория - это линия, которая идет сначала из точки А в точку В, а затем из В в С. Длина этой линии, как видно из чертежа, складывается из длин отрезков АВ, ВА и АС. Таким образом S = = AB + BA + AC = 2· AB + AC = 2· АВ + 25. Чтобы найти длину отрезка АВ, надо вычислить перемещение D s1, которое тело совершает за время D t1, уменьшая скорость от 20 м/с до 0. Для участка движения АВ мы также можем записать формулы равноускоренного движения:
0 = 20 - 10· D t1, D s1 = 20· D t1 - 10· D t12/2.
Из них получаем D t1, = 2 с, АВ = D s1 = 20· 2 - 10· 22/2 = 20 м. Окончательно, путь равен S = 2· 20 + 25 = 65 м.
При прямолинейном движении координаты и перемещение связаны формулой (это мы можем вспомнить с помощью списка основных формул) x = x0 + D s. Если отсчитывать время от t0 = 0, то промежуток времени D t = t. Тогда для прямолинейного равноускоренного движения можно написать x = x0 + v0 t + a t2/2. Оси координат у нас выбраны вверх, начальная скорость направлена тоже вверх, а ускорение направлено вниз. Значит v0 = 20, а = - 10.
В первом случае начало отсчета координат совпадает с точкой бросания. Значит начальная координата равна нулю x0 = 0. Тогда в случае а) уравнение для изменения координаты с течением времени имеет вид x = 20· t - 10· t2/2, или проще x = 20· t - 5· t2.
В случае б) начало отсчета находится на земле. В нулевой момент времени мячик находится на балконе, который на 25 м выше земли. Значит, начальная координата в этом случае x0 = 25. Получаем уравнение для координаты в случае б) в виде
x = 25 + 20· t - 5· t2.
Небольшое введение для тех, кто только приступает к изучению физики
Список основных определений физических понятий по разделу “Кинематика”
Схема взаимосвязи основных физических величин по разделу “Кинематика”
Задачи на понятия “путь” и “перемещение”
Задачи на прямолинейное равномерное движение
Задачи на закон сложения скоростей
Задачи на прямолинейное равноускоренное движение
Задачи на прямолинейное равноускоренное движение (продолжение 1)
Задачи на прямолинейное равноускоренное движение (продолжение 2)
Задачи на прямолинейное равноускоренное движение (окончание)