
Задача № 21.
Условие.
При аварийном торможении автомобиль, движущийся со скоростью 72 км/ч, остановился через 5 с. Найти тормозной путь.
Решение.

Тело двигалось, но затем, в следствие торможения, остановилось. Двигалось, по-видимому, прямолинейно (так подразумевается по умолчанию). А так как скорость в процессе движения менялась (при торможении скорость уменьшалась), то движение принимается равноускоренным. Ключевые понятия, характеризующие автомобиль в процессе торможения: скорость (72 км/ч = 20 м/с), 5 секунд (время) и путь. Итак, выписываем общие формулы прямолинейного равноускоренного движения тела, связывающие скорость, время и путь (точнее, перемещение, которое совпадает с путем при прямолинейном движении без поворотов; также для простоты обозначений пишем вместо D t просто t):
v = vo + at, D s = vo t + a t2 /2. Теперь рисуем чертеж.
Где-то с левой стороны автомобиль долго ехал к нам со скоростью 20 м/с, но в како-то момент времени водитель вдруг нажал на тормоз и автомобиль начал останавливаться. В тот момент, когда водитель нажал на тормоз, мы включили секундомер - это был начальный момент времени to = 0. В этот момент времени скорость vo была еще такой, с которой автомобиль ехал к нам, т.е. 20 м/с. Ускорение, которое в этой задаче уменьшает скорость, в течение времени t = 5 с свело всю скорость на ноль (когда тело остановилось его скорость v стала равна нулю). За 5 секунд автомобиль успел по инерции проехать расстояние D s, которое и равно тормозному пути (т.е. пути при торможении). Чтобы его найти, нам осталось применить общие формулы равноускоренного движения к нашей конкретной ситуации, т.е. для начала подставить в них все данные из условия задачи. подставляем и получаем: 0 = 20 + a· 5, D s = 20· 5 + a· 52 /2. Как всегда, внимательно смотрим на результат нашей подстановки и ищем формулу с одной буквой. Это первая формула, из которой мы находим значение ускорения а = - 4 м/с2. Знак “минус” говорит о том, что ускорение было направлено против скорости (скорость мы взяли со знаком “+”). Теперь легко находим искомое перемещение Ds = 20· 5 + (-4)· 52 /2 = 50 м.
Задача № 22.
Условие.
Уклон длиной 100 м лыжник прошел за 20 с, двигаясь с ускорением 0,3 м/с2. Какова скорость лыжника в начале и конце уклона?
Решение.
При скатывании с горки скорость лыжника возрастает, а движется он при этом прямолинейно. Значит, мы имеем дело с прямолинейным равноускоренным движением, которое в общем виде описывается двумя формулами ( t = D t) v = vo + + at, D s = vo t + a t2 /2. Пройденный путь является перемещением D s = 100 м за время движения t = 20 с. Ускорение а = 0,3 м/с2 является причиной увеличения скорости от некой начальной vo до некой конечной v. Причем, мы не можем считать начальную скорость равной нулю, так как нам нужно ее найти. Даже без рисунка понятно, что теперь нужно просто подставить все численные данные в исходные формулы: v = vo + 0,3· 20, 100 = vo · 20 + 0,3 · 202 /2. Вторая формула содержит только одну неизвестную букву (величину - это vo ). Ее без труда находим vo = 2 м/с. Тогда конечная скорость v = 2 + 0,3· 20 = 8 м/с. И все!
Задача № 23.
Условие.
При скорости 15 км/ч тормозной путь автомобиля равен 1,5 м. Каким будет тормозной путь автомобиля при скорости 90 км/ч? Тормозящее ускорение считать в обоих случаях одинаковым.
Решение.
Последние несколько задач мы решили очень быстро, описывая ход решения в краткой форме. Чтобы не забывать общую технологию решения, эту задачу снова рассмотрим по подробнее.
Итак, с чем имеем дело? С движущемся телом. Это тело рассматривается в двух ситуациях. Каков характер движения тела в этих ситуациях? В каждой из рассматриваемых ситуаций тело останавливается, т.е. постепенно изменяет свою скорость от начального значения до нуля. Поскольку каких-либо специальных оговорок не сделано, считаем движение прямолинейным. Ускорение подразумевается постоянным (и одинаковым). Значит, по перечисленным признакам можно сделать вывод, что мы имеем дело с прямолинейным равноускоренным движением. Общие формулы для такого движения имеют вид:
(t = D t); v = vo + at, D s = vo t + a t2 /2.
Поскольку у нас рассматриваются две ситуации, значит нужно нарисовать два чертежа, ввести независимые обозначения для характеристик движения тела в этих ситуациях и применить общие формулы к этим конкретным случаям. Выполняем намеченную программу действий.
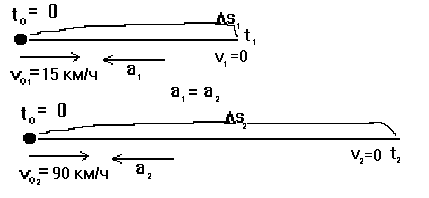
В первом случае автомобиль остановился за время t1 от начальной скорости v01 = =15 км/ч = 15· 1000/3600 = 4,1(6) м/с, пройдя перемещение D s1 = 1,5 м, двигаясь с ускорением а1. Значит мы должны записать: v1 = vo1 + a1 t1 , D s1 = vo1 t1 + a1 t1 2 /2, или после подстановки чисел 0 = 4,1(6) + a1 t1 , 1,5 = 4,1(6) t1 + a1 t1 2 /2.
Во втором случае автомобиль остановился за время t2 от начальной скорости v02 = =90 км/ч = 90· 1000/3600 = 25 м/с, пройдя перемещение D s2 = ? м, двигаясь с ускорением а2. Значит мы должны записать: v2 = vo2 + a2 t2 , D s2 = vo2 t2 + a2 t2 2 /2, или после подстановки чисел 0 = 25 + a2 t2 , D s2 = 25 t2 + a2 t2 2 /2.
После проделанной процедуры мы получили четыре уравнения:
0 = 4,1(6) + a1 t1 , 1,5 = 4,1(6) t1 + a1 t1 2 /2;
0 = 25 + a2 t2 , D s2 = 25 t2 + a2 t2 2 /2,
из которых нам нужно найти неизвестную величину D s2.
Теперь осталось учесть еще один важный факт, который был в условии. Там говорилось, что в обеих ситуациях ускорение одинаковое, т.е. а1 = а2. Раз они совпадают, то мы можем обозначить их одной и той же буквой: будем писать а1 = а2 = а. Заменим в наших формулах теперь а1 и а2 на а. Получим:
0 = 4,1(6) + a t1 , 1,5 = 4,1(6) t1 + a t1 2 /2;
0 = 25 + a t2 , D s2 = 25 t2 + a t2 2 /2,
С точки зрения физики мы всю необходимую работу проделали, но с точки зрения математики все только начинается. Вообще говоря, решить эту систему относительно искомой величины - полезное упражнение и приятное время провождение. Но для тех, кто вечно спешит, кому постоянно не хватает времени, я кратко продемонстрирую необходимую арифметику. Будем действовать последовательно.
Разберемся сначала с уравнениями 0 = 25 + a t2 , D s2 = 25 t2 + a t2 2 /2. Почему начнем с них? Просто, последнее уравнение содержит неизвестное перемещение, но кроме него там видны еще и совершенно нам не нужные a и t2 . Чтобы от них избавиться, их нужно сначала откуда-то выразить. Предпоследнее уравнение как раз может нам в этом помочь. Нужно еще решить, какую из величин a или t2 нам выражать из уравнения 0 = 25 + a t2 , чтобы потом подставить ее в уравнение D s2 = = 25 t2 + a t2 2 /2. Принцип выбора таков, нужно избавляться от той величины, которая нам мешает больше всего, про которую мы знаем меньше всего. Если про ускорение а мы знаем хотя бы то, что оно в обоих случаях одинаково, то про время t2 мы не знаем вообще ничего. Значит будем избавляться от него, будем выражать и подставлять его. Делаем: t2 = -25/a, D s2 = 25 (-25/а) + a (25/а)2 /2 = - 625/а + 312,5 а2/а = - 625/а + 312,5 /а = - 312,5/а. Уже легче, теперь искомая величина выражается простым образом через ускорение а, которое придется откуда-то искать. Откуда? Ответ очевиден. У нас есть еще два уравнения (для первой ситуации). В этих уравнениях содержится ТАКОЕ ЖЕ ускорение а. Найдем его оттуда! Делаем это уже известным нам способом, т.е. избавляемся от того, что нам больше всего мешает (от t1).
Из уравнения 0 = 4,1(6) + a t1 находим t1 = - 4,1(6)/а. Подстановка в уравнение 1,5 = = 4,1(6) t1 + a t1 2 /2 дает 1,5 = 4,1(6) (-4,1(6)/а) + a (-4,1(6)/а) 2 /2 = - 8,680(5)/а. Отсюда находим а = - 8,680(5)/1,5 = - 5,787(037) м/с2 (“-” говорит о торможении). Возвращаясь к D s2 окончательно получаем D s2 = - 312,5/а = - 312,5/(- 5,787(037)) = = 54 м.
К сведению любопытных читателей: расчеты в этой задаче можно было сделать гораздо быстрее в алгебраическом виде. Из первой пары уравнений находим D s1 = = - vo1 2/2a и аналогично из второй пары уравнений D s2 = - vo2 2/2a. Делим одно равенство на другое, сокращаем на 2а, получаем D s1 / D s2 = vo1 2/ vo2 2.
Выражаем D s2 = D s1 · vo2 2/ vo1 2 = 1,5 · 902/ 15 2 = 54 м.
Однако, пока нас с вами не сильно интересуют математические тонкости, хитрости и приемы проведения вычислений. Главное - понять физическую суть задачи и аккуратно довести до конца все необходимые действия по ее решению.
Задача № 24.
Условие.
Велосипедист начал свое движение из состояния покоя и в течение первых 4 с двигался с ускорением 1 м/с2; затем в течение 0,1 мин он двигался равномерно и последние 20 м - равнозамедленно до остановки. Найти среднюю скорость за все время движения. Построить график зависимости скорости от времени.
Решение.
Давайте, для разнообразия, чертеж нарисуем сразу (вообще-то обычно чертеж и анализ задачи делаются одновременно, ведь чертеж делается руками, а анализ мозгами и одно другому не мешает. В условиях же книги эту технологию соблюсти довольно трудно).
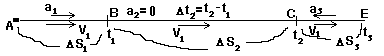
Подумаем над характером движения тела. По-видимому, велосипедист двигался все время вдоль одной прямой. Весь его путь разбивается на три участка движения. На каждом участке движения велосипедиста характеризуют СВОИ значения существенных физических величин (скорости, времени, перемещения, ускорения), так что мы должны все эти величины отличать друг от друга (по разному обозначать).
На первом участке он двигался равноускоренно (признак - наличие постоянного ускорения а1 = 1 м/с2) и за время D t1 = t1 = 4 с совершил перемещение D s1 = АВ, достигнув из состояния покоя (vo = 0) скорости v1.
На втором участке движение равномерное (признак - слово “равномерное” в условии задачи). Совершенное перемещение равно D s2 = ВС. В течение всего промежутка времени движения на втором участке D t2 = 0,1 мин = 6 с скорость тела была постоянной и такой, какой она была в начальной точке второго участка. А в начальной точке второго участка скорость была такой же как в конечной точке первого участка, т.е. v1, значит на всем втором участке скорость была равна v1. Отметьте для себя, что промежуток движения D t2 и время движения t2 это вещи разные. Промежуток движения измеряется от начала участка до его конца, а время движения t2 измеряется от начала всего движения (точки А) до конца второго участка (точки С). Поэтому, время t2 (именно его показывает секундомер, который включили в точке А) включает в себя и время t1 и промежуток D t2; t2 = t1 + D t2 = 10 с.
Когда велосипедист достиг точки С он нажал на тормоз. В этот момент времени его скорость все еще была равна скорости v1 с которой он въезжал на участок №3. Под действием тормозящего ускорения а3 он остановился (vk = 0), пройдя за время D t3 перемещение D s3 = 20 м. Его движение было равноускоренным (признак - слово “равнозамедленно”, которое означает “равноускоренное торможение”). Время всего движения t3 складывается из времени движения на самом третьем участке D t3 и времени t2, прошедшем от начала движения до начала третьего участка t3 = t2 + D t3.
Теперь можно выписать общие формулы движения.
На первом и третьем участке движение было равноускоренное, значит для их описания необходимо использовать две формулы равноускоренного движения: v = = vo + a D t, D s = vo D t + a D t2 /2.
На втором участке происходило равномерное движение, значит мы должны использовать формулу равномерного движения s = D s = v D t.
Последний шаг - применить общие формулы к нашим конкретным участкам движения. Вперед, за работу!
Для первого участка движения мы должны записать общие формулы равноускоренного движения, снабдив все величины номером №1. Получим (t1 = D t1):
v1 = vo1 + a1 t1, D s1 = vo1 t1 + a1 t1 2 /2.
Теперь вместо величин мы подставляем их значения (если, конечно, мы их знаем, а если не знаем, оставляем буквой). Имеем:
v1 = 0 + 1· 4 = 4 м/с, D s1 = 0· 4 + 1· 42 /2 = 8 м.
Разобравшись с участком №1, переходим к участку №2. Делаем аналогичные действия, записываем общую формулу с номером 2 у величин и подставляем значения (напомним, что v2 = v1):
D s2 = s2 = v2· D t2 = v1· D t2 = 4· 6 = 24 м.
Для последнего третьего участка опять нужно использовать формулы равноускоренного движения: v3 = vo3 + a3 D t3, D s3 = vo3 D t3 + a3 D t3 2 /2. Начальная скорость третьего участка совпадает с конечной скоростью второго vo3 = v2 = v1 = 4 м/с, а конечная скорость равна нулю, т.е. v3 = 0. Подставляя в формулы численные данные, получаем:
0 = 4 + a3 D t3, 20 = 4 D t3 + a3 D t3 2 /2.
С такой системой уравнений мы уже сталкивались (два уравнения с двумя неизвестными). Чтобы ее решить, нужно из простого уравнения выразить одну величину и подставить в сложное. Выразим из первого уравнения ускорение третьего участка а3, получим: а3 = - 4/D t3. Теперь подставляем во втором уравнении вместо а3 равное ему выражение - 4/D t3 и получаем: 20 = 4 D t3 + (- 4/D t3) D t3 2 /2.
Упрощаем выражение:
20 = 4 D t3 + (- 4/D t3) D t3 2 /2 = 4 D t3 - 4D t3 /2 = 2 D t3. Отсюда находим D t3 = 20/2 = = 10 с.
Теперь мы можем найти ускорение а3 = - 4/D t3 = -4/10 = - 0,4 м/с2.
Мы нашли ВСЕ физические величины, характерные для движения на КАЖДОМ участке. Это означает, что мы можем теперь ответить на любой вопрос, связанный с движением велосипедиста. Что нам нужно найти по условию задачи? Среднюю скорость? Пожалуйста! Смотрим в списке величин, что такое средняя скорость - это полное перемещение деленное на все время движения. Полное перемещение складывается из перемещений на каждом участке, значит оно равно D s = D s1 + D s2 + D s3 = 8 + 24 + 20 = 52 м. Полное время движения - это время t3 = t1 + D t2 + D t3 = 4 + 6 + 10 = 20 с. Значит средняя скорость vср = D s/ t3 = 52/20 = 2,6 м/с.
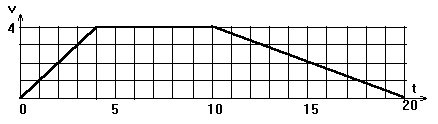
Теперь осталось построить график зависимости скорости от времени. Это сделать просто, ведь мы знаем, что в течение первых 4 с скорость увеличивалась от нуля до значения 4 м/с, в течение последующих 6 с скорость не менялась, а затем в течение последних 10 с скорость упала до нуля снова. Так что рисуем:
Небольшое введение для тех, кто только приступает к изучению физики
Список основных определений физических понятий по разделу “Кинематика”
Схема взаимосвязи основных физических величин по разделу “Кинематика”
Задачи на понятия “путь” и “перемещение”
Задачи на прямолинейное равномерное движение
Задачи на закон сложения скоростей
Задачи на прямолинейное равноускоренное движение
Задачи на прямолинейное равноускоренное движение (продолжение 1)
Задачи на прямолинейное равноускоренное движение (окончание)