This book comes from a science teacher and is addressed primarily to teachers. Any person, however – a parent, a school or a district official – who wants to participate in a current heated discussion on what is wrong with the current education (if any), and how to fix it (if needed) will find in this book many unusual and even controversial statements (Chapters 8 to 12 are addressed mostly to science teachers, but have a content which does not require any specialized knowledge, and provide ideas useful for any subject teacher).

The first goal of this book is to present a coherent description of the teaching philosophy (based on an extensive and successful teaching practice), which can be used by a teacher when planning and reflecting on his or her teaching work.

The secondary purpose of this book is to offer several unorthodox views on what is happening in the field education. That is why, while reading this book, sometimes it might feel like reading a science paper, or a political pamphlet, or listening to a person thinking out loud, or being involved into a heat discussion.

FYI: please, pardon my English, I learned it by watching TV shows, listening to a radio, but mostly by teaching mathematics and physics to college and university students.

_________________

This work has been inspired by and dedicated to Jon Stewart and Stephen Colbert – two the smartest persons in the whole world.

Chapter 1: Questions that no one asks.

My friends know that sometimes I exaggerate things.

For example, when I say that this book has everything what anyone who cares about education needs to know about teaching, my friends would know that I am making an overstatement. No single book can ever provide complete knowledge about teaching (or anything else, for that matter). However, I stick to my opinion that everyone who cares about teaching should read this book to make his or her mind about the issues discussed in it.

Can a dumb person be a teacher? Should an idiot know that he or she is an idiot?

Ask anyone and everyone will tell you what makes a teacher to be a good teacher. If everyone knows how to teach, why do we constantly hear about so many bad teachers in schools?

Why a decade after a decade the NSF and private foundations spend hundreds of millions of dollars on improving the US education and yet every new report cries about a low level of education in the U.S.?

These and many other questions have been brewing in my mind for quite some time and I am absolutely convinced should be brewing in anyone's mind, as long as one cares about teaching. We may have different answers to those questions, but we have to at least compare them hoping to find a common ground.

You might ask yourself: “Who is this guy, and why should I listen to what he says?”

To begin with, I am a teacher - like you. I am just thinking out loud; you don’t have to agree with me, in fact I’d rather prefer if you would criticize me (isn’t questioning and offering a critique is the core of the highly praised Socratic method of thinking?)

Let me tell you a little bit about myself.

I’ve got about 20 years of teaching experience. I’ve taught in two different countries, on two different continents. I’ve taught physics and mathematics, logic and problem solving. I taught courses to middle school students and high school students, to college students and university students, to students with learning disabilities, to middle school teachers and high school teachers (very often on the same day). And yet, can you imagine that right after graduating from a university, I didn’t even want to become a teacher? For me and my classmates becoming a teacher was the worst-case scenario (profession-wise).

When the Russian economy collapsed the assistant professor salary was not nearly enough to support my young family. So I began tutoring and also picking up around the city any classes available for teaching. One thing led to another and about 10 years later I got my PhD in education (with the concentration in teacher professional development, you can find more info at http://teachology.xyz/mathhealth/rezume.htm). I went into teaching for money, but I stayed in it because I found there something more than just a way to financial stability. I found the path to self-realization.

FYI: I do not teach below the college level any more, but that is not my fault. When I came to the U.S. I really wanted to work in a middle or a high school, I sent my resume to almost every US school district. Turned out it was easier to get into a college than into a school.

I am a good teacher. It took a while to realize that. I remember the first time when I noticed that I was actually not bad at teaching. A college student handed me a problem to grade (trembling hands, scared look). It was correct, and I said so. And she said, that was the first physics problem in her life she solved completely on her own.

Was I born a good teacher? Of course not! When growing up I liked reading a lot, I liked solving chess puzzles, and I played in a band. Today I realize that my childhood experiences helped me learn how to talk to people, how to reason, and how to be confident in front of a crowd. But the main reason that I’ve become a good teacher is that I had good teachers around me for the most part my life.

First I want to thank my parents; they were very patient with me. Only when I became a parent I understood how difficult it might be at times. Plus, my parents always had subscriptions to popular magazines about science and technologies. Reading those magazines as well as lots of science fiction stories boosted my imagination and fascination by math and physics.

I also had many excellent middle and high school teachers and university teachers. At that time I did not know that they were excellent. Only when I started teaching myself and started professionally observing how other people teach, I realized how good my teachers were. They knew their subjects very well.

And they demanded from us - students - to memorize a lot of stuff. But they also encouraged us to think and helped us to learn how to do that. In hindsight, it turned out, not many teachers do that in schools.

So, when I started my teaching career, I just mimicked my teachers without even realizing that. Later on, when I entered the field of professional development of school teachers, I didn’t really teach them how to teach, I just mostly shared my own experience of growing up as a teacher. And this is exactly what I want to do again by writing this book.

Please, spend a couple of minutes and read the quote below.

“University are conducting research on the relationship between mathematical knowledge for teaching (MKT), teaching practice, and student outcomes. The study of MKT is embedded in a study of the effectiveness of the Math Solutions professional development model. Math Solutions is a widely used professional development provider started by Marilyn Burns. The study builds on work of the research team and differs from earlier work in that 80 fourth and fifth grade teachers in twelve Albuquerque, NM schools are randomly assigned to either the treatment group or the control group. Randomization occurs within grades within schools. Math Solutions provides teachers in the treatment group professional development that has a strong focus on MKT. Teachers in the control group receive the typical professional development offered by the district.

This consists of a combination of summer mathematics institutes and three-to-six hour introductions to Everyday Mathematics, the instructional materials used by the schools in the study. The research questions are as follows. How effective is Math Solutions as compared to a typical ad-hoc mathematics professional development?

Does Math Solutions improve teachers’ MKT, the quality of their instruction, and/or their students’ outcomes? How are different aspects of teachers’ mathematical knowledge and instructions related to student achievement? Teacher MKT is measured by Learning Mathematics for Teaching (instruments developed by the PI and colleagues) and student achievement is measured by assessments developed recently by the PI with the NSF support. Classroom observations and video provide data on classroom instruction.”

This was a quote from an abstract of a grant proposal of a certain university (the grant received an award from the NSF).

I don’t know about you, but when I read this, I picture an entomologist looking at the bunch of ants, or maybe an Army marine biologist who studies how to better train dolphins to attack enemy submarines. “Hey teachers, this is what we are going to do to you, and then we will measure if you ever become better.”

I believe that research like this one will generate many academic papers, and reports, and policy recommendations, and future grant applications, but in the end it will not make much of a difference for students of those teachers (researches simply will move on to study new aspects of their theories).

I believe that nowadays we do not need to spend considerable amount of money to study what is teaching or what is learning or what school teachers should know.

Instead:

1. We should agree on working definition of teaching and learning and use them to propel positive changes in teaching practices.

2. We need to concentrate available funding on teacher preparation, which will result in propelling positive changes in teaching practices. The most of the book is an attempt to provide the support for the two statements above (you will also find below my version of the answers to the questions presented at the beginning of this chapter).

Chapter 2: What is teaching?

Below is the quote from Google search on: “what is teaching” (the top answer):

The second meaning of “teaching” is transparent: “teaching is a synonym for philosophy”. But the first description does not really say much what teaching is. “Teaching is what a teacher does”.

Well, what does a teacher do? And why?

In general we all do what we do for the same reasons (look up, for instance, the Maslow’s Hierarchy). Everyone wants to be healthy and successful and no one wants to be ill and poor. The only difference is how we want to achieve our success. There are people who use other people as a tool for climbing the life ladder. I would not recommend people like that going into teaching. Children feel when they are being used and always find the way to escape – one way or another. Anyone who wants to be a teacher (or an educator of some sort), should do it to help children to succeed in their life, and they will return the success.

Teaching is an important human practice. According to a general theory of human practice, an individual always acts accordingly with his or her definition of the practice. “A definition” usually means an intuitive understanding of what the practice is for, and how it should be acted. Normally, we do not give any specific reasons for why do we act the way we do. We just do.

FYI: when Socrates was asking people questions, his ultimate goal was to make them to see those internal reasons for their actions (and then to present the contradiction between the actions and the pronounced goals of those actions, which usually made people to hate Socrates – but this is a different discussion).

The reason that almost everyone thinks he or she knows how to teach is because most of the people use a very simplified (we could say – primitive) definition of teaching. In short, it sounds like “do as I say”.

This very approach is built in our DNA. Our parents used this approach when teaching us. Animals use this approach when teaching cubs, pups, baby birds (they rather use the “do as I do” version, which is also very popular among humans). Even the very people in academia who teach teachers do it using the old fashion “do as I say” way.

If teaching was indeed merely “do as I do” or “do as I say” practice, then of course everyone could do it! Teaching would not be much different from training animals (“a stick and a carrot” would do the trick).

So, why does the country spend millions of dollars on teacher preparation (and why it does not seem working well)?

First of all, clearly, teaching is something more complicated than just “do as I say”. And, secondly, not everyone can become a good teacher. Everyone can cook at home, or drive a car. But not everyone can become a successful chef or a racecar driver. And when we say this out loud, it does not sound controversial – because it’s obvious! Yes, we know that some people are a better fit for some practices than others, and some people are not a good fit for some practices.

In particular, some people just do not fit to be teachers (not their fault, by the way), and one of the goals of a teacher preparation program should be identifying those people and helping them to find another professional path (a high teacher turnaround sometimes might be not a bad thing).

So, what is teaching, or, what does it mean to be a teacher?

I believe that the answer to this question forms a fundamental basis for the whole professional philosophy of a teacher and for the practice built on that philosophy. One of the first indicators of a true teacher is that he or she has a certain answer to this question. I also believe that there is no single correct answer to this question. I believe that every teacher should search for and find his or her own answer (although the answers might sound very similarly). In this book I want to share my answer to the question “what is teaching?”.

To me, teaching is guiding students through a specifically designed set of learning experiences (a.c.a. student activities) to help them to develop or advance desired skills and knowledge – this is my formal definition of teaching (hence, a teacher is a person who teaches in accordance with this definition).

A teacher might be not the one who designs the whole set of student activities, but should have a deep understanding of the reasons for the activities and measures of the success or failure of the activities.

We all know the old saying that one can bring a horse to water but one cannot make it drink. Well, a teacher cannot make a student learn unless that student wants to learn. Unfortunately, too often students want to learn only to avoid some kind of punishment. This kind of teaching might happen when a teacher does not really care about students, but just functioning to avoid being punished himself (mimicking/faking teaching). On another hand, a teacher might be very forceful on students (“It is for your own good”) to become being praised. I believe, no matter what a teacher does, students should not have any psychological damage (like, feeling stupid). Teachers - like doctors – should take “a Hippocratic Oath” of a Teacher and promise “never do harm to anyone”, because there is always something more important in teaching than merely transmitting knowledge or training skills. A true teacher knows the limits.

Ideally, parents should be the first true teachers. The best gift a parent can give to a child is good habits and love for learning. The same is true for a teacher.

Look at infants and little children – they always try things and want to learn something new! Now look at school graduates – so many of them do not want to learn anything new anymore (or cannot learn anything new, which is even worse).

If children lost their curiosity and desire to learn, that only means they did not have a true teacher in their life.

A true teacher is not the one who just loves teaching (“do as I say”), but the one who above all loves learning. The art of teaching is based on love for education, and passion for sharing this love (and also on the science of learning).

Every student has his or her own learning style. Every classroom is different from another. Teaching constantly presents challenges: students do not act the way a teacher expects, parents or officials put pressure on a teacher. If a person cannot withstand challenges that person should not go into the business of education in any form; she/he is not going to be a good teacher, or administrator or a researcher in the field.

For centuries teaching was a very closed profession, but now this situation might change (I believe it has to change). In principle, contemporary technologies allow to broadcast live from every classroom. Everyone who wants to become an educator should imagine that there is a web camera watching him or her all day long. If that would have become an issue, this person should not go into teaching.

No one is perfect. Everyone makes mistakes (the difference is what we do after we made it - do we try to forget it as soon as possible, or we learn from it). Mistakes are an inherent part of our life. Mistakes are inevitable and unavoidable. Especially when people learn something new.

A teacher should understand that students will be making mistakes. Learning is based on continually overcoming mistakes and learning from them. If a student did not learn something, which he or she was supposed to learn, chances are that it was because a teacher made a mistake (an experienced teacher can present a long list of those).

A true teacher never stops learning (mostly because no matter how good we are there is always a room for improvement: new students are different from the former ones, world changes, a new year is never the same as the previous one).

And a true teacher is always open about mistakes he or she has done, even (especially!) if it happens in front of a class.

So, to summarize, what does make a teacher to be The Teacher? Patience, love of learning, understanding and accepting personal limits (of students and of themselves), genuinely caring for students (they intuitively feel if for the teacher they are just pawns in his/her game for personal success), constant professional development – including, but not limited to – having deeper knowledge of the content of the subject he or she teaches, deeper understanding of the fundamentals of the knowledge development within a specific science (each school subject is a projection or a simplification of a certain science), deeper understanding of the fundamentals of the knowledge development in general (including knowledge elicitation and knowledge management), understating of human behavior in general and behavior of a child, understanding of the fundamentals of human learning and teaching, and constant broadening the set of teaching skills.

From a procedural point of view, the simplest model of teaching is “teaching = motivating + demonstrating + instructing + explaining + assessing”, hence a teacher should have right personal qualities, knowledge and skills which will allow to be able to motivate, demonstrate, instruct, explain, and assess (within the limits placed by “do no harm” rule).

A true teacher is not always the one whose professional description says so. A teacher is a person about whom other people (at least one) say that they have learned something important from that person.

There is one more issue I would like to address briefly before moving to the next chapter. Many people (including policy makers, parents, business representatives) think that to be a good teacher one just needs to know the content he or she teaches. That however is not true.

The content knowledge is only one of many components of a good teacher, and not the most important one.

Firstly, I have met people who had excellent content knowledge but were terrible teachers.

I had professors who were at the top of the achievement list in academia, but who could not teach at all (they were very interesting storytellers, though). Clearly, they knew how to do difficult science and they did it. But they could not explain what they did, and why.

Secondly, content knowledge is just a result of a certain amount of effort. Any reasonable person who spends a reasonable amount of time can obtain content knowledge in the amount sufficient to teaching at any reasonable level. Personal qualities like willingness to learn till the first day of the retirement (at least), patience, etc. are much more important for becoming a true teacher. A teacher is - first - a person, and - second - a knowledge storage, a skill presenter, a guide, a trainer. If one wants to become a teacher for something more than just money, that is already a sign for him or her having right personal qualities.

Finally, let’s answer the questions: “Can a dumb person be a teacher?”, and “Should an idiot know that he or she is an idiot?”

Yes, a dumb person can be a teacher, but not a good one. We can grab a person off a street and make him/her to coach a football team.

Well, of course he/she can always tell the players: “run faster”, kick straighter”, “hit stronger”, and other obvious advices. But that could hardly be called coaching. Same is true for teaching; one does not have to be a rocket scientist to tell students “open the book”, “read this out loud”, “solve this problem”, and issue any grade which feels appropriate. But that could hardly be called teaching.

No, an idiot should not know that he or she is an idiot. Being an idiot is a medical condition, it is programed in a DNA. Everyone can and should learn to the highest level allowed by the nature, and if one’s level is lower than someone else’s there is no shame in that. There is some shame, though, in not trying to achieve the most what the nature gave.

Chapter 3: What is learning?

A dictionary tells that learning is:

* the acquisition of knowledge or skills through experience, study, or by being taught.

* knowledge acquired through experience, study, or being taught.

For a teacher this definition may be a starting point for reaching a deeper understanding of how people learn. There are so many books on this topic so it is almost impossible to say anything new. Hence, I will just try to say the same things with just slightly different accents.

The first fundamental notion is that the ability to learn is programmed in our DNA. Every healthy person can learn a considerable amount of knowledge and develop a significant volume of skills. Imagine a healthy person of any race or gender, who for the first 20-ish years of his or her life was loved by the nicest parents, did not know any economic or social hardship, was surrounded by the team of the best in the country teachers and supportive professionals. There is no doubt in my mind that that person would learn everything he or she would want to learn at the highest level of achievement allowed to attend any Ivy League University and gradate it with the perfect GPA. The reality, of course, is much different from this thought experiment. The conditions of the thought experiment state: “healthy person”, “loving parents”, “no economic or social hardship”, “best teachers and supportive professionals”. Any deviation from those conditions - and – well, we all know what is happening in the real life.

The second fundamental notion is that learning is a basic need, like food, or oxygen. The need for learning is also programmed in our DNA. There is a “slight” difference, though. With no food or oxygen a person ceases the biological existence (a.c.a dies). Without learning a person ceases the social existence (reason for all dictators to micromanage education - they are scared of free thinking which comes with true education).

Without learning one remains just a purely biological item which existence does not affect society. In this case one subconsciously feels his or her “non-existence” (from a social point of view) and struggles with it (which might be expressed in many different forms of antisocial behavior).

Learning - as a process and as a result - is solely responsible for the prosperity of a society (even if the prosperity still is very uneven). Clearly, people responsible for learning – teachers – should have respect and support from, well, everyone. Why this is not always a case? In part because too many people (including policymakers) define teaching as just “do as I say” practice: “Anyone can do it; I can do it; if I can do it why do I have to give this guy - a teacher - a special treatment?” (people usually feel respect to people who can do something they themselves cannot do).

Thirdly, learning is a process; it has phases, it has stages (that is why a college does not accept middle school graduates; although, I have seen some colleges accepting adults with the knowledge of an 8th-grader; how does teaching in a college or a university might look like, and what is wrong with the research on teaching at those levels requires a separate discussion).

Learning stages might differ in length and difficulty, depend on many parameters (subjective - like age, race, brain development of a student; contextual – what science is this subject about; social – culture, traditions, economics),but they are as objective as stages in the seasons we observe every year.

The existence of these stages results in the existence of the specific patterns of learning, which must be reflected in the specific patterns of teaching. We cannot jump from a spring right into a winter; similarly, we cannot jump into learning quadratic equations right after learning the addition within a hundred

(the normal process of giving a birth requires 9 months and should go through well-established phases - from an embryo to a baby: the process of “giving a birth” to an educated person– from having no knowledge and skills to having them at a specific level - also has specific stages and requires certain time).

If despite our best efforts a student did not learn how to solve a quadratic equation, it means that his/her learning path had missed in the past some of the important stages (assuming that students’ learnability is adequate).

Finally, learning is a result, it is an achievement. There are many achievements in our life which – kind of - just happen; learning how to walk, learning how to talk. Achievements like that happen usually in a natural way, they do not normally require special prolonged management, do not have to be controlled, assessed, regularly measured, at least if everything happens as expected.

However, reading and writing, adding and subtracting, solving equations, etc. are skills to learn which a special and longitudinal effort is required, and hence, these skills have to be assessed. What needs to be assessed, how, when and by whom, however, are some of the most controversial questions of the Teachology (a practical science of learning and teaching – what you're reading right now is my Teachology, you are welcome to borrow it or you may want to write your own).

True learning never happens by just watching and listening (i.e. by merely attending lectures), it happens by doing. You can observe every cycling tour; interview every famous racer, that will definitely help you to understand the theory of biking, but to learn how to ride a bicycle you have to ride a bicycle. You can watch for hours other people swimming, but if you want to learn how to swim you have to get yourself into water and start trying. In the latter case, it would help having around someone who could explain you what you do wrong and how to correct it (your friend screaming “you can do it, you can do it” would not be much of a help).

Lectures, of course, are not absolutely useless (if done correctly). Lectures help to boost motivation, develop vocabulary, give a perception that things are not as hard as they might be seemed. Reading (and watching, and listening) also helps to form a vocabulary, to strengthen some relationships between the current knowledge and the upcoming one, to ignite curiosity, to boost imagination, to reinforce self-discipline, to advance mental capacities.

Skills, however, are only formed by doing.

If we reverse this statement, we can say that only what we do results in formation of corresponding skills. For example, if the only exercise students had been doing for 12 years is squats, they will not be good at push-ups and pull-ups. If we want students to develop a certain skill, we have to give them an opportunity to practice that skill (ideally – as long as they need to master it).

If students do not demonstrate a skill, it means that they did not have an opportunity to do activities leading to mastering the skill.

Our brain is acting in a way our regular muscles act (I have been using this principle in my teaching since the beginning of my teaching career).

Memorization is a mental activity very much different from creating new images, searching for new meanings, describing new phenomena, or developing new approach to solving a problem: and during different mental activities a brain does a work of a different kind. Hence, if for 12 years in a school students only have been memorizing facts, it is not reasonable to expect from the graduates an ability to think critically, or to be creative.

FYI: if you want to keep your brain in shape, do not be lazy and do not go to lumosity.com, better learn a new language, or how to play a piano – any meaningful learning experience will do much more good for a brain, plus, you will get a useful skill.

Thinking critically is a specific mental activity, which requires comprehensive methodology, meticulous planning, detailed procedures, and designated time (much more time than just memorizing and retrieving facts). However, proponents of critical thinking often forget that any kind of thinking must be concrete, it has to lead to a specific goal.

Knitting together words and phrases without proving a certain point of view is a pure speculation which might seem as a creative thinking, but in reality just a fog used to cover the absence of an intellectual substance (it could be used, though, as a mental exercise at the beginning stage of advancing creative thinking to help to shake internal intellectual barriers).

Whether we like it or not, but this is a fact: within the limits placed by the current standards, curricula and learning environment critical thinking development does not fit in the regular teaching process (advocating for critical thinking without advocating for significant changes in the structure of teaching process – including its budgeting – is just a wishful thinking).

Another commonly discussed issue is the absence of transfer of learning. In many papers it is described as a case when students solved a problem they had been taught how to solve and could not solve a modified problem. In different forms, one can find similar statements again, and again, and again. Tons of books are written on transfer of learning. A teacher as a practitioner does not really need to read all of them to study all possible theories and approaches. A teacher needs a working model, which he or she can immediately use and gradually advance based on the experience and reflection. I happened to develop a theory which works for me, and which can be used by any teacher as a starting point.

FYI: a theory – any theory – is simply an intellectual tool, which we use to organize our actions; while it works, we use it; when it stops working, it is a time for a new one – just like a hammer.

1.Transfer of learning is a myth, it does not exist. If one learned how to perform a task, one can repeat it in the future as many times as one has to repeat the same task. The key word is “the same”. Our brain is a powerful pattern recognition machine (and as any other skill the pattern recognition skill also can be trained).

As soon as a brain recognizes the task, it retrieves from the memory the sequence of the actions, which has to be performed to succeed.

Of course, we assume that that particular brain is capable of storing and retrieving information and governing actions required for fulfilling the task (otherwise we have to discuss a case of learning disabilities).

If a brain does not recognize the task, we have two options:

(a) the task is the same but due to some features it is camouflaged as a different one - transfer of knowledge is not required (required actions are recognition, retrieving and reapplying);

(b) the task is indeed different (at least in some parts) and is really new for the brain and the brain does not have the solution (at least in full) in its storage – hence there is no knowledge to transfer (naturally, we could talk about how much the new task is different from ones done in the past, but this conversation is not directly related to “knowledge transfer”).

FYI: a word “a problem” has so many meanings, so I redefined it for my own purposes; by my definition, if a person has “a problem” to solve and knows the solution and just have to apply it (retrieve from the memory and re-act), it is not a problem - it is a task; if a person does not know the solution and has to create it – this is a problem. Using this language, there are only two situations: (a) one has to perform a task – no transfer of knowledge is required; or (b) one has to solve a problem by creating a new (for the person) procedure, i.e. one has to create a brand new (for the one) solution; of course, one must utilize some of the knowledge previously stored in the memory and we could call this action “utilization of previous knowledge”, or “reactivation of previous knowledge”, but “transfer of knowledge” would not be just the right term to describe this situation.

2. Every teacher has to teach students to two different practices: (a) how to perform specific tasks (the set of those tasks should be specified by a curriculum); (b) how to create a solution to a problem which has not been solved in the past (by that person); the latter practice, in turn, requires a practice in making a conclusion regarding the familiarity of the given assignment - is it the same as one from the past (is it a task?) or different (is it a problem?)? Development of such a skill also requires specific practice (hence, time; hence, money).

Teaching thinking critically (a.c.a. creatively) means teaching how to create/invent solutions (actions, procedures) which have not been presented/trained before (at least in full).

Now we can see, that - in general - the answer to the question “what is learning?” depends on the personal interpretation of who is asking this questions.

For example, one can believe that learning is …

1. memorizing facts and excelling in performing certain task (actions).

Or one can think that learning is …

2. obtaining knowledge and developing skills which will allow to create (a.c.a “construct” – for those who loves constructivism, as I do) solutions to problems which have never been solved by the person in the past.

My personal definition of learning is a combination of the two above (in fact, I am sure the true learning in accordance with the second one automatically includes the first one; true creativity is always concrete and based on solid knowledge).

From a procedural point of view, the simplest model of learning I use is:

Learning = goal making + memorizing + reiterating/practicing + thinking/analyzing + self-assessing (reflecting on the actions done during the problem-solving process).

A teacher should be able to facilitate in students all the components of learning (an example of actions a teacher can use for facilitating problem solving process in physics is given in Chapter 9). Goal making represents a transition from “I do not want/care” to “I want to do it”. Memorizing is responsible for the transition from “I do not know” to “I know”. Training, practicing is responsible for the transition from “I cannot do it” to “I can do it”.

Thinking is responsible for the transition from “I do not understand it” to “I got it!”. Reflecting is responsible for the transition from “I am confused” to “I learned it!”.

I believe that teaching how to think critically, teaching how to create solutions to new problems is the most important goal and the most difficult task of the contemporary education. If a person cannot solve a new (for that person) problem, it is hard to expect this person would generate some knowledge (or product, or business) new to the society.

However, if a person can solve problems which he or she has not solved in the past, there is at least a chance that that person would give us something absolutely new and unexpected (good or bad – that is a different conversation). We should keep in mind, though, that critical thinking cannot be learned without a solid foundation in facts and skills, and requires much more time than rote memorization.

Chapter 4: What do we need and what don’t we need to research?

Many teachers are involved in some kind of research directed toward better understanding of how to teach better. My view is that a teacher has to play the central role in guiding the research. In order to do that he or she does not need to have an advance degree in education or psychology; a teacher needs to have his or her own working (and loud) opinion on what research is and what he or she wants from it.

All sciences are equal, but some are more equal than others (paraphrasing George Orwell).

The history of science teaches us that every science evolves through similar stages and gets a substantial boost when its fundamental principles and common practices had been quantified (such highly quantified fields as math, physics, chemistry come to mind).

Teachology, as a practical science of learning and teaching is still in its infancy. Using the language you can often find in IQ tests, when comparing the current condition of Teachology with what it should become in the future we can say “Teachology to science is like alchemy to chemistry”.

Yes, we know a lot about learning and teaching; yes, we have many handy rules we can use when developing our teaching policies and strategies, but we still do not have a comprehensive theory of learning and teaching which has predictive power – a cornerstone of a true science (and many people still believe in the existence of a “silver bullet”, “a magic wand”, or of “a philosopher’s stone” if you will, a.c.a a perfect teaching process which will solve all the current problems we see in education – all we need is to discover that process and train all teachers to use it).

FYI: the fact that engineering has a comprehensive theory behind it (physics) and education hasn’t does not make people who do education less respectable, or smart, or socially important than engineers (or any other professionals); as well as the fact that a comprehensive theory of education does not exist yet does not make researchers working on the building of this theory less respectable, or smart, or socially important than physicists (or any other scientists).

On the contrary, doing education (teaching) and conducting research in education is harder than doing physics (precisely because physics is already a well established science, but Teachology is not).

A “simple” question – what grade each student will have at the end of the year – cannot be answered (try asking this question to an educational scientist teaching you how to teach, and then ask, if a science cannot make a prediction, is it really a science?). A better question would be – this is my class, what specifically should be done to assure that each student will ace the material? and two following questions - how much time should that take? and what resources must be utilized?. A comprehensive theory of learning and teaching must provide clear answers to these questions. I believe, that everyone would agree that having such a comprehensive theory of learning and teaching is exactly the reason the government must finance research in education. And the government had spent on this research millions and millions of dollars (check nsf.gov). So, why those millions did not help to improve education to the desired level?

Well, at first you can ask, who said the education has not improved?

The answer is – the government! Just search online for “statistic on education in the U.S.” and read the first top ten web-sites. For example, below is a quote from https://www.dosomething.org/facts/11-facts-about-education-america (not a government site but uses its statistic):

“11. High schools are not preparing students with the skills and knowledge necessary to excel after graduation. Only 1 in 4 high school students graduate college-ready in the 4 core subjects of English, reading, math and science.”

We all want to believe that the money the government issues to researches really helps to bring education to a new level, but I, personally, could not find solid evidence of that.

What I found is papers which goal was to prove that students with good teachers do better than students with not so good teachers; students in small classes do often better than students in large classes; students in poor neighborhoods do on average worse than students in richer places. Results of such kind of research often find a place on TV or radio. And every time when I see such a paper I ask myself - do we really need to spend money to prove that having a good teacher is better than having a bad one?

If a team loses a game, after a game, after a game, a year, after a year, every team owner always does the same thing, i.e. replaces the coach. Everybody knows that a good coach is the first condition for any team to perform well. We can discuss what does it mean to be a good coach, and how to find a good coach, and how to keep a good coach, but we do not want to waste money to study if a team can win without having a good coach – because it can’t, and because it is obvious!

Soon after I started teaching in the U.S. I learned about FCI (Force Concept Inventory). First time when I used it I just asked students to do it at the beginning and then at the end of the semester. I observed some gains, which of course made me feel good. Next time, though, I incorporated most of the questions from FCI into my lectures. Do you think that (a) that instructional action affected the post-semester gains, and if you think it did – (b) how do you think it affected them? For anyone who has the slightest teaching experience this is no-brainer; of course, after I had incorporated the questions into the instructions the post-semester gains went up. What does this prove? This proves the simple fact that when a teacher teaches - students learn.

If learning did not happen, there are only two reasons for that: (A) a teacher did not teach properly, or (B) a student was not capable to learn. In the latter case we also have only two options: (a) a student had some intellectual/mental/brain-associated deficiencies; (b) a student did not have appropriate background (which means, the student was not properly taught in the past and the teacher did not take it into consideration, which really brings us again to case (A)).

I believe that anyone who can learn how to use a multiplication table and how to solve a quadratic equation is capable of learning quantum gravity (just as an example of something considered very difficult): there are only two reason for that not to happen, either the lack of the desire from a student, or a wrong teacher.

When a teacher teaches (appropriately to the student abilities, of course) – students learn. Students do not learn what is not being taught (or self- taught, for the sake of generality). These statements (laws, principles, postulates, axioms) are obvious and do not require specially funded research.

And yet, one can find papers like: “we divided students into two groups, in one group students were instructed to learn that, in another group students were not instructed to learn that, the result is, students in the first group learned that, and students in the second group did not ”.

I do not think a teacher participating in this kind of research would benefit from it. I do not think this kind of research deserves special funding. I think, though, that a teacher should be able to recognize this kind of “research: and say NO to it. A teacher also should read some scholarly literature, but should be very critical to what he/she is reading (an example of such critical reading is given in Chapter 13).

Let us go back for the moment to the quote from a grant abstract I presented in chapter 1.

This consists of a combination of summer mathematics institutes and three-to-six hour introductions to Everyday Mathematics, the instructional materials used by the schools in the study. The research questions are as follows. How effective is Math Solutions as compared to typical ad-hoc mathematics professional development? Does Math Solutions improve teachers’ MKT, the quality of their instruction, and/or their students’ outcomes?

How are different aspects of teachers’ mathematical knowledge and instructions related to student achievement? Teacher MKT is measured by Learning Mathematics for Teaching (instruments developed by the PI and colleagues) and student achievement is measured by assessments developed recently by the PI with the NSF support. Classroom observations and video provide data on classroom instruction.”

This is my translation of this abstract into a plain English: the researches want to study if a math teacher needs to know math. Of course, if they would have said just that, they would not get any funding. Hence, a beautiful scientific language. The authors most probably would argue that they wanted to study what specific math knowledge a math teacher should know. Well, I can give an answer to this question – for free! I teacher – any teacher, should know the material at least two levels above the level he or she teaches, for example, a fifth grade math teacher should be confident doing a seven grade math (at least). This is the minimum requirement. Ideally every school math teacher should know math at the introductory college level (same should be true for any teacher of any subject).

I hear people screaming: “how do you know that, do you have evidence?” Yes, I do – from the observations of hundreds of teachers, but more importantly, from my own teaching practice (please, check chapter 1).

For our current discussion, however, it is not important if you trust me or not. You do not have to trust me at all. You should trust your logic.

Scientific process is based on a hypothesis and facts, which in the end either support or oppose the hypothesis (a littlie bit more on a scientific method is in Chapter 13).

Let us treat my statement above as a hypothesis. Then, let us train teachers in math to the selected level (we know from the school curriculum what math should be learned). Then let us measure learning outcomes of the teachers’ students. If they are at the desired level, my hypothesis was correct.

Otherwise, well, what first comes to mind is the teacher did not get a good training, or this person is not fit to be a teacher, or the new students were very different from the students in the past, or ... (I am sure you can add at least a couple of more possible reasons).

Now we need to make a decision on what might went wrong and how to fix it. You may say that this does not look like a scientific research any more, and you will be absolutely right, because it is not! Just bear with me for a couple of more minutes and I will try to explain what I mean.

If teachers are getting training, in the end their skills have to be assessed. But to assess math knowledge and skills there is no need for developing a special tool (like Learning Mathematics for Teaching), a standard final exam will do the trick. Did the training affect learning outcomes of the students? Let us look at the grades students getting from those teachers. You do not trust the assessments the school district uses to measure students’ learning outcomes? Let us make better assessments. You do not know which teacher training program is more efficient, Math Solutions or a “typical ad-hoc mathematics professional development”?

At first, let us compare the full textual description of each and see if there is any difference; and it will be clear if there should be any significant difference in the teachers’ outcomes. If you expect one program will give a much better result, just drop another one. Or, finally - which would be the best way to compare any programs of professional development - let teachers choose, they are smart and capable of figuring out what helps them do a better work, and they talk to each other.

FYI: teachers (as anybody else) may need to feel some pressure to get into professional development. If a teacher does not really care what kind of professional development program to attend, maybe (a) this person should not be a teacher, or (b) the teacher needs a better a supervisor.

Naturally, this approach does not represent a pure scientific research any more. Which is why it is better! It guarantees positive changes for students (and teachers, of course) without spending money on things which do not have any practical purposes.

There is no need for Learning Mathematics for Teaching, there is a need though for robust tools to measure math knowledge of anyone at all levels/stages/phases of learning math.

The practical realization of this approach, of course, requires much more detailed planning, and a lot of political will.

Thank you for bearing with me. I will try to describe now why we do not need some of the current research and what should be done instead.

In general, there are three kinds of human practices with the goal of advancing human life: (a) scientific research - the goal of a scientific research is discovering new knowledge; (b) engineering and art - the goal of an engineering development is building new devices (systems of devices), the goal of art is bringing artifacts of art; (c) social advancement - the goal of a social advancement project is developing or adopting new collective practice(s). Since all three practices/projects have different goals, they all should be managed differently.

Clearly, every practice has some elements of a scientific research: when we start a project, we generally have some understanding of what we want to achieve and how we want to achieve that (“a hypothesis”), and how will we assess (measure) how close we are to the goal (“facts”).

But if we want to induce some societal change, we have to initiate and manage a social project. Social progress is the result of innovative practices of people doing something new - to them – which they did not do in the past. Scientific progress is the result of practices when people do something new to a large part of human culture (a.c.a. “science”). A scientific research might be a part of a social project, but the goal of the project should dominate the formulation of the research questions.

An innovator, i.e. a person who is a subject of an innovative practice, does not always have to be a researcher (and v.v.), but when an innovator and a researcher work together on achieving a positive societal change, the goals should be stated by an innovator.

Many of the projects “imposed” on teachers are social projects by their nature, and should be treated and managed as such. Only in this case there will be visible results - not just for the authors and their scientific colleges, but also for the teachers and most importantly for students.

Knowing all what I said above about research, a teacher can (and should) respond to a researcher with his or her view of what a project should aim at, and how to access the success of it.

For a teacher the ultimate goal of any project should be not just a paper with his or her name as a subject of an experiment, but the improvement in learning outcomes of students.

It does not mean, however, that there is no fundamental research left to do in education. There are lots of fundamental questions to study, and every teacher can be a part or a principal of such study.

If I had to select what to fund I would start from looking around for a list of fundamental scientific facts and relationships that had been discovered in the science of education over the last two or three decades, and then for the list of questions that should be studied now and answered as soon as possible (an analog of the Hilbert’s list of problems). The first thing I would ask every researcher applying for a grant is what is his or her version of this list, and how his or her research is connected to the fundamental questions to be answered by the research community. If they give an answer, that is a research project (belongs to the NSF), otherwise the project is social (belongs to N Social F?).

FYI: every teacher also can and should ask every researcher – when met - for such a list.

My view is that everyone who applies for a grant to fund a scientific research in education should demonstrate the use of the scientific method developed in physics, math, chemistry, but applied to study phenomena in the realm of education.

Nowadays, when a physicist is trying to understand how the nature works, he/she uses clear terminology and well-defined measuring tools and procedures. He or she starts from building the simplest model which reflects some of the most important features of the system under study.

In many cases to begin building such a model a physicist starts essentially from building up a classification table of the objects and processes under study (a model is a loaded word, but essentially it is some kind of a description of some part of the nature - verbal, graphical, mathematical, etc. – which we use until the model works, and then we refine it or we replace it with a better model).

In education everything is happening with people and in people (in their brains and muscles).

The number of different kinds of learners (different by age, gender, race, social background, economic background, intellectual background, language, motivation, learning abilities and psychological characteristics) is finite. The number of combinations of different learners in different class settings is also finite. The number of scientific subjects to learn is finite. The number of stages for each subject to be learned (and, hence, the time to learn it) is finite.

For any subject, the process of learning it has a finite number of steps, elements, “atoms”. Hence, the “grand classification table of learning spaces and trajectories” has a finite number of elements, and, hence, needs a finite time and resources to be developed. If developed, it would have answered a question: “for the given type of a student, and for the given learning and social environment, what learning activities should the student perform in order to master the given subject?”

FYI: as a simple initial model I would treat the “learning space” of students in any class as (essentially) three dimensional: students might differ by their 1. background (previously learned knowledge and skills); 2. learnability (rate and volume of attaining and retaining knowledge and skills as a function of time and effort); 3. motivation (aspirations, willingness to learn – very often related to the cultural background of a student).

I believe that if the government really wants to move the needle in education, it has to change its own approach to funding the fundamental research in education. In particular, it has to set specific long term but achievable and measurable goals (the Manhattan project, or the Apollo program come to mind as examples of such approach). For example, the development and study of the mentioned above the “grand classification table of learning spaces and trajectories” could be one of such fundamental researches.

As a part of the fundamental research I would also suggest to study how “Taylorism” can be used as an instrument to improve teaching practices.

Please, do not take me wrong, I do not think that teachers should be acting like robots performing a strictly specified sequence of activities and spending strictly specified time on each action. On the contrary, I know that would be a disastrous approach.

What I think is that - since every learning action, every learning experience takes a certain time (which depends on the type of the learner and the learning environment) - we need to know how much time it might take for learners of different types to learn each “atom” of a subject, so we could better plan and perform teaching activities using for each student the most efficient ones.

It is obvious (i.e. does not require a specifically funded research) that presenting an algorithm for solving a quadratic equation takes much less time than guiding students toward developing such an algorithm.

If we knew how much time, on average, under average conditions, for an average student would take to absorb each required fact (including very complicated ones), and master each required skill (including high level of intellectual work), we could do better everything we do today in education.

The government spends billions of dollars on collecting the ocean of information about citizens. It could spend some on the money on collecting data on students (anonymously , of course); race, edge, gander, short term memory, long term memory, concentration, attention span (lots of instruments to measure such feathers had been developed since 1960-s), and correlate with grades, and with social parameters of the learning environment.

If there was strong political will it could have been done (the “Manhattan Project” and the “Apollo Program” again come to mind).

Finally, when we talk about education, we talk about controlled teaching, i.e. about teaching managed by a certain person – a teacher (naturally, people also learn on their own, but we will not discuss how that kind of learning might affect the controlled one).

Every single thing a teacher does, every teaching action, every instructional move also takes time.

Teaching practice also is composed of “atoms”. If we want that teachers could manage teaching practices effectively and efficiently, we need to know in the fist place how much time a teacher (of a certain type – which are different) spends on each “atom” of his or her teaching practice.

As we can see, there is a room for fundamental research in education. Teachers, however, do not have to become scientists and get deeply immersed in a fundamental research (unless they want to; in fact, a practitioner who becomes a scientist is usually the best kind of a scientist from R&D point of view). A teacher should reflect on his or her work from the point of view described above, i.e. analyzing the factors, which affect learning of his or her students and his or her own teaching practice.

A teacher also should be able to tell a researcher if the offered research does not help him or her to teach better (which means, a teacher should know what he or she needs to learn and to have in order to teach better).

The way I see things is that research like quoted twice before looks to me as a waste of money – from the point of view of the societal change it will make, of course.

FYI: naturally, “a waste of money” is an exaggeration. But if it was up to me, I would rather give those $ 4.7 million dollars to those 80 teachers, so they could spend the money on their professional development. The social outcome would be much greater.

Coming back to the question, what do we need and what don’t we need to research, my answer is – unless the research aims at the fundamental questions discussed above, we do not need it. Instead, we need to fund projects directed toward specific societal changes, mostly related to teacher professional development. Unfortunately, the shift from funding purely scientific projects to funding social projects does not happen as fast as needed. If you ask me - why, my answer is, I don’t know. My guess would be (a) traditions, (b) ambitions.

Chapter 5: What do we have to do to fix the issues reported in every report of the last decades?

I have to admit from the beginning, that I do not know how to answer the question in the title of this chapter. I also do not believe that there is anyone who does. But I do have a couple of suggestions based on my understanding of the general theory of human practice (in Russian, the name of this theory is “Methodology”, like “a science about methods – in general – for improving human practice of any kind”). Plus, I also believe that every teacher should have an opinion on what is wrong with education in general and how to fix it (it should be a part of his or her teaching philosophy: what is teaching, why is it important, how it should be done, how it should be governed, what is learning, etc.).

First of all, economy, financial situation, money distribution trumps everything else. Until teachers’ conditions, including wages, will be the same as in the best schools in the country, talking about significant changes in the quality of teaching is merely wishful thinking (hence, spending money on something else would be mostly a waste). Miracles do happen, but not en masse (that is why we call them a miracle).

If I had to make a choice what to finance: education or research on education, I would choose education (until teachers’ conditions, including wages, will be the same as in the best schools).

One however can dream. Imagine that there is plenty of money for everything. In that case we can ask what would be the most efficient way to finance different projects on advancing education.

In any profession, or more broadly, in any human practice, The Master is the one who, among other qualities, knows criteria of a successful work, can articulate the criteria and uses the criteria to measure his/her own success. The latter means constant reflection on what has been achieved and how to do it better (and did the criteria worked or they may need to be modified)? The same is true for organizations. That is why it is critical for every teacher, and every professional involved in education, to reflect on his or her work, what has been achieved, what went wrong, what to do differently, etc.

(For instance, the NSF (or maybe an independent party) should do a research on how the NSF finances a research, was it worth to spend money the way it was spent?).

Every institution which invests in education should draw a clear line between scientific research projects (which mission is developing new knowledge) and social projects with the mission to advance social changes.

In education many projects which proposed as a research are social by their nature. Social projects have to be managed and judged based on the social goal they propose to achieve. That includes the way money should be distributed to the participants.

Albert Einstein famously said that doing the same thing over and over again and expecting different results is insanity. One of the recurring activities funded on a regular bases is revising curricula. The common motive is: “the world has changed, so should what we teach”. Yes, the world has changed. But mathematics (physics, chemistry) hasn’t so much.

Content-wise, more than 95 % of what students should learn in STEM courses remains (and will remain for quite some time) a constant of education.

If we want to incorporate some new hot topics (robotics, networks, etc.), the fastest, easiest, and the cheapest way is just to allow teachers to choose 5 % of the curriculum and teach anything they want during that time (of course, approved by the officials), and to provide opportunities to choose from offers coming from universities and other providers of professional development programs.

We know from many reports, which say it over and over again, that the quality of education is not sufficient, that the quality of teaching is not as a good as needed.

Maybe it is a signal that we are doing something the same over and over again, which does not work? Maybe it is a sign to try some new approaches to fixing recurring problems? For example, let teachers to decide how to advance their professionalism?

Education is a big industry, it is a huge market.

Many people (at least in the U.S.) believe that free (but fair) market should be able to satisfy the demands of the consumers. Who is the consumer and who is the supplier on the educational market? It is usually agreed upon that the teachers are the most important suppliers and we all (as taxpayers) are consumers. That is why we demand from teachers the best teaching results (and to know the results we – via the government – develop various systems to measure it).

But no one is born to be a good teacher (chapter 2).

Becoming a true teacher takes time and effort. Everyone who wants to become a good teacher has the right to demand the best available training. Everyone who wants to become a good teacher becomes a consumer of the teacher professional development system. I believe that teachers should be granted money which they can use on their own professional development. Probably, money should not go to an individual teacher directly but to a some kind of a teacher association (a union?).

That association should be placing orders for various teacher preparation activities/programs, and also keep track of the effectiveness of those programs (government officials should keep track of the results of teaching and make them openly available, and parents should keep teachers to be accountable for the results of teaching). To advance the preparation of the current and future teachers we all need to start trusting them with the way they improve their work (trust, of course, should be balanced by verifying that the results of their work show an improvement).

Instead of experimenting on teachers (will they learn something or not if we make them do this and that?) universities (and other providers) should reach out to teachers and ask them what do teachers need to be developed (in exchange for the money the teachers have from the NSF or other sources), or market to teachers already developed solutions.

Don’t we usually say that the best way to teach someone to take responsibilities is making the person to be in charge? Maybe it is time for teachers to say: “Let us make in charge for our own professional growth”?

The key problem of contemporary education is not an insufficient teaching, it is an insufficient teacher preparation.

Effective, productive, sufficient teacher preparation will result in effective, productive, sufficient teaching (assuming the economical issues are resolved). This statement does not require research. Using scientific way of thinking, we should take this statement as a postulate, as an axiom, and start using it to make social changes we need.

For example, the absence of effective, productive, sufficient teaching is the sign of the absence of effective, productive, sufficient teacher preparation. What should be done in this case? My version sounds like this: “Hey, Teacher, I am the Union, here is money, go and become better prepared! (but, please, keep in mind, if you fail, we will have to let you go)”.

There is no mystery in the minimum of what every teacher has to know. Does a teacher teach math in 7th grade? If yes, no doubts (no research needed!) he or she must know the math at least for all grades up to and including the 7th.

Teaching math to a 7th grader and teaching it to a teacher who teaches in 7th grade, however, are two different things requiring two different strategies. No doubts, a teacher should have taken a course about teaching math, and a math course.

But the math course for a teacher has to be multi-dimensional; while learning math a teacher also should exercise in reflecting on how he or she learned it, so a teacher would know how the new math knowledge had been developed (produced, internalized, trained) in his or her own brain (of course, this kind of a course would require more time, hence would be more expensive!). And this is the kind of professional development course a teacher should demand.

If we rely on market, what the government should do?

The first duty of the government is to fulfill the fundamental financial needs of the education: buildings, books, equipment, wages, etc.

Imagine for a moment that all teachers and officials are the best in the field and do not need any further preparation, and there are no vacancies for any position, how much would it cost to provide to all schools across the country the same top level of financing? This number should be the target number for the government.

The second most important duty of the government is to establish an efficient comprehensive system for assessing students’ learning outcomes (people rightly say “what can’t be measured, can’t be managed”). Imagine unthinkable: all 50 states have different temperature scales (or standards of mass, or time) and they do not have conversion factors, hence, measurements done in one state cannot be understood in another state. Sounds kind of ridiculous, doesn’t it? Imagine now that all 50 states have different currency, and there are no exchange rates, there is no way to use money from one state in another one (what’s left is just using barter).

This situation is even more than just ridiculous, it is impossible! And yet, this is exactly the current situation with measuring learning outcomes of students. In an ideal world any parent, teacher, official should be able to compare how a child is doing at a school relative to any other child anywhere in the country.

Imagine what a strong motivation to do the best he/she can would a teacher had if at the end of every year everyone could see how his/her students performed comparing to the rest of the country!

To be fair, everyone also should see what was the initial background of the students, how much the students gained. You may agree with the concept, but think that in realty it is impossible to create such a measuring system. Well – yes and no. Technically it would have been a very easy task to develop such a system for STEM subjects (Chapter 10 offers one possible approach).

Ensuring the wide spread adoption of such system, though, could be very hard. One source of the resistance would be “I do not believe it will work”, “we have never done it before and we are fine” (page 24: (a) traditions). Another source of the resistance would be “who are those people?”, “we know better how to teach our students” (page 24: (b) ambitions).

Until teachers begin demanding working, open, and uniform system for measuring learning outcomes I do not except any significant improvements in learning outcomes on a large scale.

I would also expect standardized test making companies to lobby against this approach because currently they make a lot of money by selling those.

Lastly, I want to address a problem of school management. A regular public school, or a private school, a pilot school, or a charter school is only as good as its principal.

Every good school administrator, as any good manager, has to know rules of the “game” (laws, instructions, official prescriptions governing the functioning of his/her administrative unit, e.g. a school), has to have people skills, be a good motivator, has to know how to determine the current state of a system (is the functioning goes at a normal level or there are issues?). But one of the most important abilities of a good manager is “seeing through people”.

A manager manages people who have different experiences (and many other qualities), but most importantly, (a) who have different aspirations, professional goals, and (b) who have different professional abilities and limits. For a teacher, having a desire to a constant professional growth is a must have quality; and for a principal, stimulating this desire is a must have effort (my doctoral thesis shows, in particular, how to help a principal to see teachers who want to grow professionally and who just make an impressions that they want to).

A good manager can perform a “position analysis” and see who in the team is an innovator, who is an imitator, who is reliable, and who can make people feel good, who is a cooperator and who likes to work alone, etc. The term “a position analysis” came from a game of chess, where chess masters can just look at the board and see how the position of each piece make it or other pieces strong or vulnerable, maneuverable or confined. Similarly, a manager can see a professional and communal position of each member of the team and direct his/her ensemble toward a mutual goal in the most effective way.

Since teachers tend to work alone behind closed doors, but the success of a school as a whole heavily depends on how they work as a team, the ability to preform a position analysis is especially important for a school principal.

We need good school principals as badly as we need good teachers. Everything what I said about teacher preparation can be directly applied to professional development of school officials. But there is something more, which could be done (at least in theory).

What happens to a firm if it goes bankrupt? Usually, another business buys it, it changes the owner, a new owner supposedly is more efficient, knowledgeable, productive (otherwise he/she would not have money to buy the failed firm in the first place). The best way to deal with a failed school would be putting if for “an auction”, but not for a sale, of course.

A failed school could have become a branch of another school managed by a successful principal (especially if managing more students and teachers would be reflected in the principal’s wage).

The winning principal would be one of several principals competing for taking over the failing school (and he/she will find and train his/her "proxy" to manage failed school, who will become another good principal). Only if no other acting principal wants to take over the failing school, in that case the government should step up and overtake it.

I do understand that this approach would break the current system of financing the schools ( (a) traditions), and could lead to turf wars ( (b) ambitions), but if it works for everything else, it should work for schools, as well. I also believe that teachers can and should influence the process of selecting or promoting school principals (through teacher associations).

Chapter 6: “To test or not to test?” This is NOT the right question!

Anyone who is interested in the fate of education reform in the U.S knows about the heated debate around standardized tests ongoing in all media. The most of the media share a sentiment which sounds like: “all current data show no big improvement in student learning outcomes expected after NCLB had been voted for, the reason for not having expected growth in learning outcomes is that teachers have been teaching to a test, the reason for teachers teaching to a test is NCLB, hence, we have to change the law and take out standardized testing”.

First: I would like to point out at a contradiction no one seems to notice: if teachers do indeed teach to a test, why are test results so low? If you want to pass a driving test, you study questions and you practice, and as the result you get your driver’s license. Why does not this happen in math, or reading, etc. (for decades!)? Is it really a problem with using tests, or there is something deeper, which should be addressed?

I have a feeling that there are people who are looking for a scapegoat to explain why after 14 years of implementation of the law and hundreds of millions spent on it the state of education has not changed as much as it was expected. And here it is – testing! After testing became mandatory, teachers failed to teach! Well, “after that” does not mean “because of that”. If teachers have been teaching to a test and tests results are low, blaming tests for that should be the last thing to blame.

Second: I do not know a single author who would loudly said: “I am against accountability in education, we do not need to know what students learned”. If someone would have said that I would understand his or her position and would argue why accountability is important and should be the part of the system. But if an author is not against accountability in education, he or she is automatically for measurability in education, and has to offer his or her vision on what to measure and how to measure.

It means in turn that the author has to critically analyze the current system used to measure learning outcomes of students and to offer a specific way to improve it, or should describe a brand new system which should be used to replace the current one.

The same approach should be adopted by everyone who is criticizing teachers and school for not teaching students creativity. Every adept of developing critical thinking skills (for example) should either (a) state that he or she does not want to know if students actually had the skill developed, or (b) offer a specific instrument for measuring the skill, or (c) accept the fact that he or she does not know how to measure the skill he or she finds the most important for students to have.

There is no paper criticizing standardized testing which would offer a specific solution to improve the situation. But they all have a common factor, they all call for investing more money in education. Having not enough money becomes another common blaming target. But there is no such thing as enough money, there is no industry or human practice where people would say: “Stop, we do not need more money any more”.

Of course, education needs investments, but how do we know that new money will make change we need, considering that old many did not make it? The structure of investments is more important than the volume, and teachers have to be given a right to veto investments which they think will not help them teach better.

A vast amount of money goes somewhere around education, to study what a 7th grade math teacher needs to know (I suggest the answer, he or she needs to know math at least as the 7th grader), for developing new tests (happening every year, in every district, or a state or at the federal level), for rewriting standards (99 % of the topics students need to learn in math, physics, chemistry has not changed for more than a century, do we really need brand new standards every few years?).

The new version of the law has to address the fundamental principles for distribution of the funds across the system of education, constructing the hierarchy from the top (buildings, teacher wages, teacher preparation, communications, textbooks), to the bottom (everything else).

A question “do we have to continue using standardized test?” leads the discussion away from the actual issues which have to be addressed and resolved.

At first, everyone has to make a clear statement against or for accountability, and then talk about mechanisms, procedures, tools which should be used to let us know (if we want to know) what students learned.

And in the end, someone, somewhere has to take a look at the current structure of expenditures related to education (on all levels) and tell us which did and which did not help students to learn. Otherwise in about 10 years the upcoming reincarnation of the law will be criticized again for not making the change everyone would have hoped to be made. And again everyone will be blaming teachers for that to happen. Unless teachers take the stand now.

Examples of the sources for this chapter:

1. Reauthorization of the Elementary and Secondary Education Act: Time to Move Beyond Test-Focused Policies, By Kevin G. Welner, William J. Mathis, Feb. 2015, http://nepc.colorado.edu/publication/esea

2. Why reports of progress on No Child Left Behind rewrite may not be a good sign

by Valerie Strauss, Mar. 2015, http://www.washingtonpost.com/blogs/answer-sheet/wp/2015/03/12/why-reports-of-progress-on-no-child-left-behind-rewrite-may-not-be-a-good-sign/

3. Five reasons standardized testing isn’t likely to let up

by Valerie Strauss, Mar. 2015, http://www.washingtonpost.com/blogs/answer-sheet/wp/2015/03/11/five-reasons-standardized-testing-isnt-likely-to-let-up/

4. New York Times Fails Education Reform – Again, by Daniel Katz, Mar. 2015, http://danielskatz.net/2015/02/22/new-york-times-fails-education-reform-again/

5. In Defense of Annual School Testing, by Chad Aldeman, Feb. 2015, http://www.nytimes.com/2015/02/07/opinion/in-defense-of-annual-school-testing.html?_r=1

Chapter 7: Why have hundreds of millions of dollars been spent on developing the common core math standards if content-wise they are not much different from the ones they replace?

I have already voiced my opinion that teachers need to be a critical force in making decisions on money distribution, as long as the money even remotely related to improving results of education. In this chapter I want to present an example of a vast waste of money, which – ideally- should have been prevented, probably by teachers (and for teachers – because those money could have been used for their professional development, for example).

The radical reformation of the U.S. system of education started after the Russian Sputnik orbited the Earth. Since then every President claimed continuing the reform as the national priority. Hundreds of millions of dollars have been spent. Every decade (on average) the Congress considers a new bill to continue the reformation (and numerous laws had been passed by the states). Naturally, the world does not stay still and education has to catch up with the changes, but if we single out one parameter of a success - learning outcomes of students, even after fifty-ish years of reforms there is still a lot of work to do.

According to the Trends in International Mathematics and Science Study (nces.ed.gov/TIMSS; the picture below shows the results for 2011) the U.S. score is nine points above the world average, but the U.S. is still behind Korea, China, and even Russia (which economy has been in shambles for decades).

Considering the fact that an annual U.S. educational budget is almost ten times greater than the Russia’s, we have to make a conclusion that the amount of money invested in education does not matter as much as the way it is spent (i.e. distributed). If we want to avoid another decade(s) of spending hundreds of millions of dollars and not seeing a significant improvement in learning outcomes of students, we need to analyze the reasons for not having a significant improvement in the past.

I. If we want to improve the results of teaching, we have to change the way we invest in teacher preparation.

Remember an old joke? A policeman approaches a drunken guy crawling around the side-road light and asks, “Sir, what are you doing?”. “I am looking for the keys to my home”, the guy says. “It should not be too hard to find them at such a bright place” says the policeman. “I didn’t loose them here, I lost them over there”, says the guy. “For the God’s sake, why are you looking for your keys here, then?”. “Because”, says the guy, “it is brighter here.”

Where have we been looking for the keys to the educational reform?

The list is long. Charter schools, early college high schools, new textbooks, new standards, bringing tablets in classrooms, providing high speed internet, just to name a few.

Of course, the infrastructure matters a lot. But textbooks, or tablets do not teach students, teachers do. If the percentage of good teachers does not increase, nothing will help to increase learning outcomes of students nationwide. New charter schools will just affect the distribution of teachers between schools. New textbooks will not be used effectively by inefficient teachers.

The # 1 investment (maybe not by the volume but by the priority) should not be an investment into infrastructure but in teacher preparation. This kind of investment currently is also vast and systematic, no doubt. The quality of teaching, however, remains to be not as good as everyone wants (report after report is criticizing the quality of teaching – for decades). Two questions immediately come to mind: why, and what to do about it?

Let’s use an analogy again (the joke above was an analogy, too).

A space shuttle really looks like an airplane.

However, it is impossible to invent and to construct a space shuttle just by making airplanes better, and better, and better. Even the very idea of a spacecraft (including a shuttle) cannot be derived from the ideas which had lead to the creation of airplanes. Scientists and engineers had to find an absolutely new principle to just start thinking about the possibility of getting off the Earth.

For making a drastic change in improving the quality of teaching we have to find today a new leading principle to guide the reform of professional development of teachers.

Here I want to repeat my statement I made in Chapter 5: “The key problem of contemporary education is not an insufficient teaching, it is an insufficient teacher preparation. Effective, productive, sufficient teacher preparation will result in effective, productive, sufficient teaching (assuming the economical issues are resolved)”.

This statement does not require any research. This statement is a postulate.

All people reading this book are deveined now into two camps: the ones who accept this postulate as a postulate, and the other ones. There is nothing wrong with this, this is how any science works; the future will show who is right (if we accept this postulate and base our actions on it and the actions lead to the “better world” the postulate becomes a law, otherwise, it will be replaced with a different one and eventually will be forgotten by everyone except historians).

Naturally, as the author of the postulate, I base on it all my future logic (and my current actions).

The first consequence from this postulate is a statement that the absence of effective, productive, sufficient teaching is the sign of the absence of effective, productive, sufficient teacher preparation. Which means, in turn, that the current system of teacher preparation does not work, or at least is very much ineffective.

What should be done about it? How can we make a qualitative change in teacher preparation? My version of the answer to this questions sounds like this: “Hey, Teacher, I am the Union, here is money, use it to become better prepared! (but, please, keep in mind, if you fail, we will have to let you go)”.

Until teachers become true and demanding customers on the teacher professional development market, they will be fed by many “professional development” activities which will not help them becoming better teachers.

II. Research in education only matters if it targets the ways of teaching.

Let's carry out a mental experiment. Let us assume, hypothetically, that we put together a group of the best in the world designers of car wheels and gave them everything they had asked for to do their job. Then we had separately formed a group of the best designers of car engines.

And we had independently formed a group of the best car body designers. Etc., etc. All the groups finally had developed the best car wheels in the world, the best car engine in the world, the best auto body in the world, etc. Now, ask yourself, what would had happened if we tried to put all these best auto parts together? The obvious answer is - nothing! They would not match each other, they would not fit with each other.

The absolutely same situation is happening now within research in education. Someone writes a fine textbook for middle school students. Another person independently writes a collection of problems for high school students. A third person creates an electronic encyclopedia for students at the college level, etc., etc. Each didactic tool can be helpful for a certain group of students, but they do not match each other! Hence, they will not make a visible change in the overall results of teaching.

Why?

Learning is a long and complicated process. As any process it has stages and phases, which are based on sequences of learning actions like “reading a text of the problem”, “making a sketch”, “listening to a teacher”, “writing a question”, “observing data”, and many others. Each learning action takes a certain period of time (different for different type of students, by the way). An effective/efficient learning process obeys the certain timing.

This means that an effective/efficient teaching process must obey the same timing.

However, if you read papers on education, you will not find one which would discuss the timeframe of using a newly invented learning tool. Maybe this textbook or that collection of assignments is good on its own, but a teacher is just unable to fit those teaching tools in the existing timeframe of teaching. If a teacher would try to use all newly developed learning tools in his/her lessons, the whole learning process would be just broken. But using just a single new element will not make a big effect on learning outcomes of students.

Instead of trying to decompose the learning process into individual “learning atoms” and time each of them to depict the exact structure of a learning process, the main research effort is concentrated on creating more and more new but functionally disconnected teaching tools.

The main reason for this “crisis of variety” of educational instruments is that to this day there is no social force which main goal would have been “forcing” researches into cooperation: funds go to almost anyone who offers a new and existing initiative, but there is no one who tries to connect them together and direct toward a mutual goal.

Ask yourself, what factor united all scientists, engineers, generals and all the staff of Manhattan Project? If you said “The mutual goal”, it would not help much, because it would not be specific (too general). And such a goal as “Making a new highly destructive weapon” could pretty much separate people because people may have different ideas of “highly destructive weapon”.

But, the goal “Making a U-bomb” made people united because this goal had an absolutely specific outcome – an atomic bomb - which “everybody” could see, touch, use - the clear and measurable outcome.

Analogically, “Making a good education” or “Improving education” is not a uniting goal. But “Making a certain/specific educational environment” could be the one. The measure of achieving the goal would depend on the specificity of the goal, i.e. on the learning environment chosen to be created.

A goal like that, when achieved, should lead to a visible impact on the system of education. It should be replicable.

It should be related to a learning process of a large entity of the system. My view is that the “specific learning environment” should be composed of a set of classes “vertical” within one school – for example, one class for each elementary/middle/high school level. That would require a work of a large team of teachers. I think that teachers should ask for this type of research and even refuse to participate in research which addresses only small and local problems.

III. Any reform happens only when there are people who want to make it happen.

Please, answer the following question (and be honest to yourself): “Which social group has “improving learning outcomes of students” as the goal # 1 for every member of the group?”.

The goal # 1 for a politician is to be reelected. The goal # 1 for a school or district official is to have the contract resubmitted. The goal # 1 for a parent is to have a healthy child. The goal # 1 for a teacher is to keep his/her job.

Whether we like it or not, we all are governed by the instinct to survive – as a biological entity, and as a social entity. Every biological system, including human beings, functions in such a way, which allows it to be alive as long as possible (exemptions are rare and do not represent a healthy subject).

To be alive a biological system must utilize some resources like food, for example. Where can a biological system get food? Only from the outside of itself (it cannot eat itself and keep a long life). In the social world “outside” means from other people. But instead of taking an actual food or something else, we take money as the universal equivalent for goods.

When other people give us money, usually it is not a gift, usually they want something in exchange. So, the logical sequence is simple; to support our life we need resources; to get those resources we need money; to get money we need to give away to other people something they need from us.

In short: to support our life we need to be needed.

To be needed is the strongest motive for our activities, which is imprinted deeply inside of our human nature. This motive governs 90 % of brain activities hidden from our consciences.

Our brain (but not us) can “feel” if there is a risk for becoming “not needed” any more, and starts looking for any way to escape that kind of a risk – even if consciously we do not have any suspicions of what might happen. As the result (one of many), we do what we are getting paid for. I mean, not what we are told we are paid for, but literally, what we are paid for by people who want something from us - as our brain sees it.

I understand that I described a very primitive model of human behavior. But this model is pretty much sufficient for our discussion of what should we do to reform the reform. And the first conclusion we should make is that people involved in education should be paid for the results of their work as educators.

We the people want from our teachers, school principals, district officials high learning outcomes for our students. Hence, we have to pay them only for high results the students achieve (“the merit pay” comes to mind).

Hence, in the first place, we need to know the results as accurate as possible. Hence, we have to talk about measurability of the learning outcomes.

This is a very hot topic. The biggest problem – as I see it – is that almost everyone who is involved in the discussion has a strong opinion (different from others’) what and how should be measured. We have again a huge variety of tools used in different states, districts, at different levels.

Teachers, students, parents are overwhelmed just by the sheer volume of the tests. As the result, we see a strong resistance to even the idea of testing.

The solution is not getting rid of testing, but making testing reasonable. The very first and the hardest thing to do is to change the approach to the development of testing materials.

I propose that tools and procedures used to measure learning outcomes of students must satisfy the following conditions:

(a) Every aspect of the development and the use of the tool has to be open to public (including teachers) and be able to be examined by anyone.

(b) The use of the tool must lead to gradable information on student’s skills and knowledge.

(c) The use of the tool must lead to gradable information on student’s skills and knowledge which must not depend on any features of the teaching or learning process and which must allow to compare on the uniform bases the learning outcomes of any and all students using the tool.

(d) Any institution adopting the tool becomes an active member of the community, which can propose possible alternations to accommodate changes in the understanding of what students should know and be able to do.

It might seem impossible to develop measuring tool, which satisfy these conditions. But it actually can be done (Chapter 10 offers a possible approach in physics, which can be transferred to other subjects).

Officials at the federal or state or even district levels should not use their own measuring tools, but should rely on the same system of collecting data on learning outcomes of students used by a school.

Quizzes, tests, exams a teacher uses during a year and at the end of a year should be sufficient to make a conclusion on the quality of teaching. Development of such a system should be an immediate goal of the government.

Let’s assume the new system to measure learning outcomes of students is in place.

Should we start using it to differentiate teachers’ pay?

No! (I know I gave a different answer just several paragraphs above, but I did not really meant it, I just wanted to offer a very common logic, which I will disprove right now).

The survival instinct is so strong that the most expected outcome of direct connection between the teacher wage and the learning outcomes of students is faking good results to cover poor ones (just recall all the movies where a bad guy from the CIA wants to blow up civilians pretending terrorists would did it only because the government wants to cut the budget – the similar idea of faking things to keep to be needed, and also actual cases of correcting students’ test results).

The merit pay will not affect weak teachers the way we want.

The idea of the merit pay is based on the assumption that the strongest motive to do a good work is the fear of being fired. But this assumption is wrong. Hence, the statement I made above that “we have to pay them only for high results they achieve” is wrong (the word “only” makes it wrong; and I did it on purpose). Yes: “we need to be needed”.

We want to be needed. But humans are social beings, and “to be needed” for us is more than just “being paid”, it is “being accepted as a professional”, it is “being respected as a teacher”.

Let’s assume the new system to measure learning outcomes of students is in place.

The next step is making all the results open and available to anyone.

“I am a teacher, and anyone in the world can see how my students performed last year, and how my students perform now. But I should be paid the same wage as another teacher who teaches the same subject, at the same level, the same amount of hours, to the same number of students. I also know, though, that if another person can do my job better than I, I can be easily replaced.

That is why I always want to learn how to do my job better. That is why I need extra money so I could buy for myself a good professional development course”.

A teacher has to become the central force for reforming the reform.

Researchers, officials, politicians are not really interested in significant improvement of the system of education (at least, directly). “We need to be needed” – remember? Imagine unimaginable: every school is perfect, and every teacher is a top notch professional, and all students really learn all subjects. Many people would not be needed any more. Subconsciously we know that for many of us constant reformation is much more socially “profitable” than the finished reform (“profit”, of course, means more than just money, it is also a respect, fame, recognizability, power, …). That is one of many possible reasons for us to see new standards written every several years.

The latest incarnation of the standards is “The Common Core Standards” (CCS) developed by “The Common Core State Standard Initiative” (http://www.corestandards.org/).

I make a claim that the hundreds of millions of dollars spent on the development of CCS for mathematics is mostly a waste of money. The vast part of mathematics we want our students to know has not changed for decades (if not for centuries). The stages of learning math also have been known for decades and cannot be changed more than by a little: you cannot teach quadratic equations right after finishing teaching addition within a hundred – it would be waste of time.

Hence, if you place on a table the new common core standards and the one they replace, and compare them side-by-side, the difference in the content of math students have to learn will not be more than several percent (I think no more than 7-8 %).

If the content prescribed by the new standards is not much different from the content prescribed by the old ones, what was the point of spending millions?

The supporters of the CCS say, that the new standards provide a better structuring of the material and focusing on developing critical thinking skills. The latter statement is a wishful thinking (at best) because no one can reliably and on a large scale measure such skills.

Better structuring of a material means using a different language for describing the same knowledge and skills.

It makes some difference for researches – they can claim a novel way for describing math. But it does not make much difference for teachers. They still have to teach the same content. And finally, standards do not measure learning outcomes. Hence, even having the same standards states and districts can use absolutely incomparable measuring procedures – exactly as they have done it for decades before.

Some people say, the key word in “CCS” is “common”. Finally, the states will have a common ground to promote and assess education.

First – again – the standards do not measure the learning outcomes (see above).

And second – there is no need for spending hundreds of millions of dollars for having a common math standard. Since all current math standards are essentially the same, the governors could have just taken 50 pieces of paper, write on each the name of a state, put them all in a hat, shake the hat, and pull one piece out. Done.

So, why have hundreds of millions of dollars been spent to achieve almost nothing?

The shortest answer is: the force of habit.

Problem? => Let's pour money on it. Let's splash money around, some of it will stick to a right person at a right time.

If you are a teacher, do you think this approach is working for the school you work in, or if you are a parent do you think this approach is working for the school your kid goes in, especially considering the fact that the total government debt is about a quarter of the GDP? I don’t think so.

IV Some comments

P.S. I used to teach Physics at a small for-profit college. My students were smart and hardworking, but 99 % of them had serious problems with simple Arithmetic, and even more serious problems with Algebra.

The only reason for that is that my students were taught in a wrong way (so, I had to re-teach them). When I read a publication on how to improve education, I see the huge gap between what researchers are talking about and the every day needs of teachers. It seems to me that the vast part of money spent on research in education does not really help teachers to teach better.

P.P.S. There is The Theory of Multiple Intelligences, which is becoming more and more popular among educators. One of the reasons for the growing popularity of the theory is the interpretation which sounds like “You can’t think? Relax, you can run pretty fast”.

This approach implies that a poor teacher has a good excuse for the poor teaching job done in a class. It is a huge trivialization of the fact that human beings are capable of solving complicated problems in different fields including sport, music, design, art etc. But the fact that a person likes to dance more than anything else and can do it better than anything else does not mean that the person cannot or does not have to learn the multiplication table. The only reason that a good sportsman does not know basic Algebra (if it happens) is the poor performance of the math teacher (who in this case has to be responsible for the intellectual damage done to the student by the poor teaching work). There is a definition of “a good physical health” and if a doctor has some damage done to the physical health of a patient, the doctor gets punished very hard. It is a time to define “a good intellectual health” and to start worry about intellectual health of the Nation.

P.P.P.S. Personally, I think that the most effective tool/environment for reforming the system is an On-Line Open Public School (at least a high school). The School has to be the combination of Internet, TV and in-paper teaching instruments. Anyone (at least potentially, as “a horizon”) should be able to get an education from a scratch to the level enough to pass SAT-I (at least). Focusing the efforts on that kind of a goal gives us - as the outcome - a logically and technologically connected grade-to-grade sequence of educational instruments.

P.P.P.P.S. There is a reason why politicians are suspicious to the role teachers might play in the reform.

Teachers are conservative by the nature of their job (the subject they teach has not changed much over long periods of time). Hence, the government turns to researches: “Dear professors, please, tell us what do we need to do to teachers to make them teach better?”. I would not say that this approach is working. The government’s job should be making teachers to want to grow but still feel safe, making teachers to want to demand from researchers new good teaching tools and providing financial support for that. The hardest, the most important, and the most promising job of the government is creating the system in which a teacher would be constantly motivated for a continuous improvement of the results of his or her work.

P.P.P.P.P.S. “Be careful what you wish for, it might actual happen”. President Obama wants that every high school graduate could get into a college and get a degree. The fastest way to achieve this goal is to accept into any college anyone who wants to enter and to print out a diploma for anyone who asks – just merely based on the fact of asking - done. But is this really what Mr. Obama wants? Of course not. What he really wants is having everyone to have the high level of knowledge and skills. Let’s say one more time: “the high level of knowledge and skills”. Without having a tool to measure the desired level this goal is unachievable. And another thing: until the majority of high school graduates does have that knowledge and skills, which allow them to succeed in a college, there is no much sense to talk about any research on college education at all (except its economics).

P.P.P.P.P.P.S I worked at a college, which had accreditation but accepted students who could not solve a simple 8th-grade math problem. Since then I do not trust the current accreditation system any more. Teachers should have a goal (one of many) of making sure their students would succeed in a college. But I think teachers also should have an opinion on how a college should teach their students, and what to do to make the college work better.

Chapter 8: What does “thinking as a physicist” mean?

Learning happens in a brain (and muscles). When we teach science, we teach to think, to discuss, to make a point. Different subjects use different way of thinking. Even if the general logic is the same for all sciences, each also has a specific set of reasoning techniques, tactics, approaches. A history teacher should be able to describe what does “thinking as a historian” mean. A chemistry teacher should be able to describe what does “thinking as a chemist” mean. As a physics teacher I can only describe what does “teaching as a physicist” mean, but I believe, even if a history teacher (or any other teacher) reads my description, it might help him or her to formulate his/her own description of the way of thinking within the subject they teach.

For me, the visible result of being able to think as a physicist is in ability to solve problems. I have heard many times (as thousands of other physics teachers) a student saying that he or she understands physics but just cannot solve problems.

I always say in return, that physics is one of the clearest (and I would add easiest) subjects, since it has a very straightforward logic which underlines the thought process. However in order to teach how to solve physics problems a teacher should not be focusing on demonstrating how to solve specific physics problems (!), but instead should demonstrate the thinking process happening when an expert problem solver is constructing a solution for a given problem (this approach, however, requires much more time than a regular course can provide). When a student does not know how to solve a problem, he or she should not ask a question “how to solve this problem?”, or “how did you solve this problem?”, but instead should ask a question “how did you come up with this solution?”. And a teacher should be able to demonstrate the thinking process of the creating that solution.

There are specific learning aids, which can help a student to begin solving a problem and to keep him or her on the track till the solution is found (Chapter 11 offers some examples).

In this Chapter I want to offer a short description of a general thinking process of an expert physics problem solver.

Not everything in physics requires understanding – this is a common misunderstanding. Students often say: “I do not understand”, but in actuality it usually means: “I do not know the basics”. There are many important physical concepts, which do not require understanding, but require rote memorizing; in a standard physics textbook all those concepts are laid out in paragraphs “facts to learn” (or similar). Well, of course, some understanding is required at this level, for example, understanding of the meaning of the words and sentences (that is why I do not write in Russian the book aiming at American students). The set of the facts to be memorized comprises that knowledge, which someone might mean when saying: “I know physics”.

The next level of understanding comes when students are making connections between the just learned concepts (which might be of an abstract kind) and their knowledge of everyday life, which came from their every day experience. The existence of these connections makes students to say: “I understand physics”. This level of understanding might help students to explain some phenomena they observe around them, but usually is not enough for making them being able to solve physics problems.

The true (actual, complete) understanding underlines the ability to apply previously accumulated knowledge for analyzing new specific physical situations and comes with the experience of solving specific physical problems, and then reflecting on the process of the creating the solution.

This level of understanding is tested by the ability to solve physics problems not congruent to previously solved problems (please, visit http://teachology.xyz/mocc.htm for the difference between congruent, analogues, and similar problems).

This level of understanding demonstrates the existence of strong connections between knowledge (acquired using rote memorization), and actions, which have to be performed in order to solve a problem.

The best (and only!) way for achieving this kind of understanding is solving physical problems. Learning solving physics problems is like learning how to drive a car, or how to swim; no one can do it just by watching how other people do that; it requires a lot of personal practice, preferably guided by an experienced instructor.

If you read a text of a problem and you know what to do, it is not really a problem; it is rather just a training exercise, a task. A real problem happens when you do not know what to do and have to construct the solution on a spot.

As I often like to say, study physics without solving problems is the same as learning how to swim with never entering in water. To learn how to swim is necessary to swim, i.e. to lie down on water, start moving hands and legs, and see what happens. At the very first time, certainly, you will fail; you will drink some water and move to nothing, but gradually, a try after a try you will be doing better and better. And the time will come when the first actual swim is accomplished! You can swim now!

Precisely the same situation happens when you need to find a solution to a physics problem (and, actually, to any other problem in life). To learn how to solve problems it is necessary to solve problems, i.e.: to read a text of a problem, to imagine as clearer as possible a described situation, to draw a picture, to write down formulas, and to try to make sense of them. And of course, at some point in construction your solution you might get confused or make a mistake. Getting confused and making mistakes is a natural thing when solving problems (any problems). I make even stronger statement: making mistakes is a necessary element of learning how to solve problems. True learning actually gets triggered only when a mistake had been made and we start thinking about how to correct it (people say “learn from your mistakes”, but in reality there is no other way to learn!). Of course, when we make a mistake, we usually feel some discomfort (one of the legacies of a poor schooling).

We need to be able to overcome that discomfort. In fact, we need to embrace it, because this is the sign of a true learning happening in us.

The felling will pass and be replaced with the joy of having problem solved (the # 1 goal of any teacher is to lead a student through these emotional stages; “make physics fun” is a wrong and misleading approach because it will not leave students with knowledge and skills, the right approach is “make physics joy-able”).

The folk wisdom tells: “If you didn’t succeed first time, try and try again”. This rule is partially correct. If you keep doing the same thing you keep repeating the same mistake. Every new trial has to be in some way different from the previous ones.

That means that when you make a mistake you should figure out what went wrong (or at least to make a guess what might have gone wrong), so you would not repeat the same mistake again, i.e. you should reflect on the thinking you have used to get to this point in your solution.

The very first difficulty many students run into when they have to solve a problem is “how to begin”? My usual answer is “try something, anything”.

Let's assume, that you are invited to a party. You come, and there are so many unfamiliar people over there. What do you usually do in this kind of a situation? You usually are trying to find somebody familiar and approach him or her.

The exactly same thing is happening when we start solving a problem. Our brain is a powerful patter-recognition computer, and the first thing it does in a problematic situation is starting looking for familiar patterns. And it finds them, even if we do not feel that way. So, if you do not know what to do, your brain knows, so just trust it and do the first thing which comes to mind, but DO IT!

Of course, you can help your brain to find the appropriate pattern faster and with more confidence by using various learning aids (the general algorithm for developing a solution, a picture, a MOCC, a dictionary, a classification table).

When you are looking for a familiar person, your brain automatically analyzes a set of indicators, like a face expression, a voice, talking manners, a gait, a shape of a figure, etc. Every physics problem has some indicators/parameters, too, which differ one problem from another, but also which combine similar problems into a certain cluster of problems. When you recognize to which cluster this problem belongs, you can immediately employ the method you used in the past for solving similar problems, or at least you can try using similar strategy, reflect on it, and correct it, if needed.

Physics studies specific phenomena, i.e. specific processes happening to various objects.

Phenomena are the first things we all observe from our birth. We feel a lot of things: we can see, we can smell, we can touch objects and hear sounds. And we have developed many words we use to describe these phenomena to each other. But in science we have to use a specific language, which represents a purified/simplified/specified version of an every day language (the main reason for using a specific language is to minimize misunderstanding between scientist).

Hence, when we read a text of a problem we often have to make a translation from an everyday language to its scientific version. This is a skill which every expert problem solver has, and which can be trained, too.

Another important thing to remember when solving physics problems is that in physics we NEVER can solve any real world problem, because all real world problems are simply too complicated (because in the real world “everything is connected to everything” and the number of connections is huge)!

We always must make some simplifications, some assumptions, which make the situation described in a problem being manageable. Instead of actual objects we use idealizations, i.e. abstract objects, which do not exist in nature but have the same important properties as the real objects in a problem. For example, we do not draw the Earth to scale keeping its exact shape with all the oceans and continents, we just draw a sphere.

When solving a problem, it is important to make a clear statement of the assumptions which are made, because (a) our solution is limited by these assumptions, and (b) if something goes wrong, maybe it is because one of our assumptions was incorrect and we have to rethink them.

Since we do not deal with the actual world, but rather with an imaginary world which, in a way, is a reflection of the actual world, having a good imagination is as useful as being good at math.

Physics studies what happens to the objects around us and why. Some objects are huge, some tiny, some very fast, some not moving at all. We use a specific language to name physical objects (using nouns), to describe their properties (using adjectives), to name processes happening to the objects (using verbs) and to describe the properties of the processes (using adverbs). Any textbook gives a sufficient description of that language and how to apply if for describing the physical world.

Every word in that text has a very specific meaning and everyone must know that meaning exactly/literally; usually we call such special words/terms as physical quantities and use letters (a.c.a. variables) for a short representation of those quantities in the equations we write. Each equation represents a specific connection between quantities/variables.

Physicists, as all scientists, are always looking for patterns. A pattern is a process which repeats itself (as long as we do not drastically change the conditions describe in the problem).

When we find a pattern (might take a while to prove it is actually a regular pattern of nature), we call it “a law”. We use laws to predict what might happen under certain circumstances and to build devises, which we want to use for our purposes. Ideally, a law should be written in a mathematical form, i.e. as an equation, so we could use math to derive our predictions (and we could use the laws to form a MOCC). In physics there are only two fundamental kinds of equations: every important equation in physics is ether a definition or a law (and we have many other derived from definitions and laws combined).

A definition is basically an agreement between all the physicists in the world on the meaning of a quantity/variable. Definitions come mostly from observations of the phenomena happening to objects.

In physics, a law is a well established mathematical connection between quantities/variables (previously defined); laws come from experiments specifically designed to test those laws when they have not been called “a law” yet, but just “a hypothesis”.

Of course, there are many additional relationships which are derived from laws and definitions by algebraic manipulations, which also might be very useful when solving problems (memorizing those relationship might save valuable seconds on an exam).

As soon as we laid out all the definitions and laws related to a problem, we can start manipulating with them for creating a solution of a problem, we can reflect on our way of thinking and make a correction (if needed), and after practicing in doing all this we become experts in solving physics problem.

Let’s provide a short example of thinking as a physicists. Let’s say, we need to find the speed of a meteorological satellite which is orbiting the Earth. At first we recognize in this problem the following situation: there are two objects - the Earth and the satellite, and we assume that there is only one interaction in the system (gravitational attraction).

The Earth is not moving (another assumption), the satellite makes a circular motion with the Earth at the center of the circle (another assumption).

Key concepts for recognizing the physical situation described in the problem are “gravitational attraction” and “circular motion”. We know, that “attraction” is a kind of interactions and interactions give rise to forces, and forces are related to motion of objects via the Newton’s second law. We also know that for an object making a circular motion there are specific relationships between its kinematical variables (for example, speed, acceleration, radius).

This information is already enough to start constructing the solution.

We can draw a picture, we can write the equations we have mentioned, and start manipulating with the equations until we get a relationship between the speed of the satellite and other important parameters of the problem. If we got it, we are done, if not, we start looking for a missing link or for a mistake in our previous reasoning.

Many of students taking my courses are pre-med students.

For those students the importance of taking a physics course is far beyond getting prepared for a MCAT (in fact, a MCAT is a more complicated exam than any of the elementary physics exams).

For not physics major students the most important outcome from study physics is assessing their own personal abilities to guide their own thinking process when solving a problem – any problem.

There are deep similarities between the kind of mental work a student taking physics course have to do, and the kind of mental work a med students has to do when becoming a doctor. Some of the similarities shown in the table below. A teacher should be able to tell students what kind of mental work commonly used when study his or her subject is similar to mental work required by some common professions.

I am absolutely sure of the existence of a direct correlation between an ability of a person to learn elementary physics and the ability of that person to treat people (or, for that matter, to do any high intelligence work; I would love to teach a one semester physics course for business majors). I would not like very much if my physician had less than A- for the taken elementary physics course (as well as my financial adviser).

FYI: similarities between the kind of mental work a student taking physics course have to do, and the kind of mental work a med students has to do when becoming a doctor.

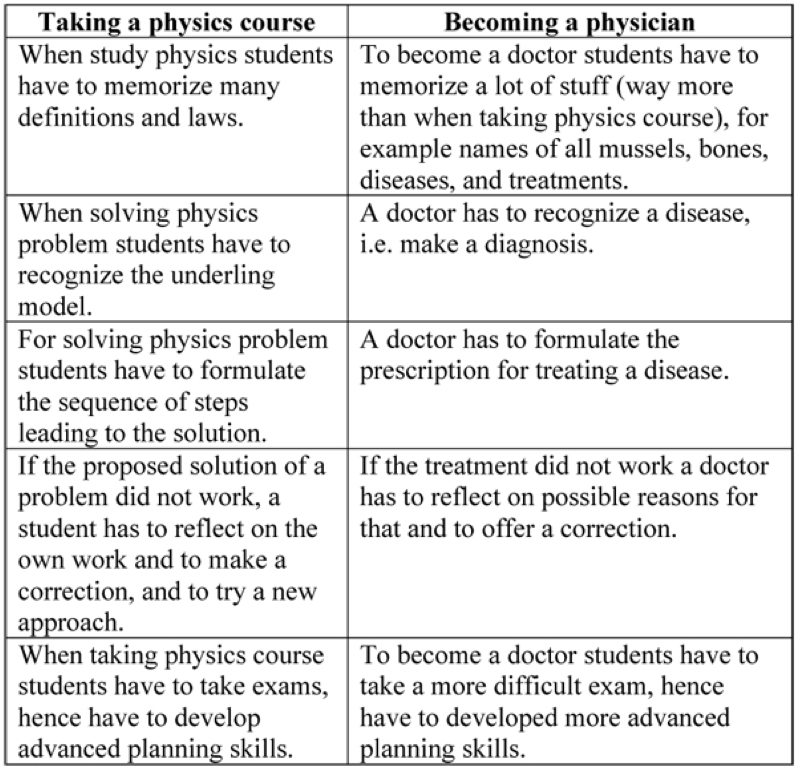
Chapter 9: A General “Algorithm” for Creating a Solution to a Physics Problem

This chapter is a continuation of the talk started in Chapter 8. Every teacher should know and be able to describe the way of thinking within the subject he or she teaches. I have developed some specific learning aids which might be useful sometimes for facilitating a problem solving process of a student taking a physics course. Similar learning aids might be developed by teachers and for teachers in other subjects.

My learning aids are based on my theory of learning (mostly covered in Chapter 2). There are many other theories on how to teach students to solve physics problems. A theory – any theory – is simply an intellectual tool, which we use to organize our actions; while it works, we use it, when it stops working, it is a time for a new one – just like a hammer.

My theory, which works for me, and I hope, might work for you, too.

First I want to remind the difference between a problem and a task.

If a person has “a problem” to solve and knows the solution and just have to apply it (retrieve from the memory and re-act), it is not a problem - it is a task; if a person does not know the solution and have to create it – this is a problem.

Every teacher has to teach students to two different practices: (a) how to perform specific tasks (the set of those tasks should be specified by a curriculum); (b) how to create a solution to a problem which has not been solved in the past (by that person); the latter practice, in turn, requires a practice in making a conclusion regarding the familiarity of the given assignment - is it the same as one from the past (is it a task?) or different (is it a problem?)? Development of such a skill also requires specific practice.

Hence, teaching how to find a solution means - before all - teaching how to recognize the old task in the new one and to apply the appropriate method (which worked in the past).

Teaching how to create/invent solutions (actions, procedures) which have not been presented/trained before (at least in full) means teaching thinking creatively (a.c.a. critically).

Although due to the definition of “creativity” the act of creating something new should be seen as the result of an insight, a teacher can help a student to get to that insight as close as possible using the “algorithm” described below.

This “algorithm” is for a teacher, who is guiding a student.

Part III of the “algorithm” (“Logic of creating a solution”), however, can be offered to a student as a printed guide in order to help him or her to begin the thinking process.

I. Psychology of creating of a solution.

1. Convince yourself that the problem has a solution (no one starts acting unless he or she believes “this can be done!”, or being forced into acting).

2. Convince yourself that you can create the solution of the problem (no one starts acting unless he or she believes “I can do this!”, or being forced into acting); it is not really important can you do it absolutely independently or with engaging of somebody’s help (teacher’s, friend’s); convince yourself that it is possible to think about the problem, to do some actions related to the solution of the problem, to reflect on your actions.

3. Formulate some simple operations/actions you can perform, some steps you can do to begin a solution, something that is possible to do right now (under the conditions described in a problem).

4. Make a choice of what action are you going to do right now and do it ("enter into a cold water").

5. Keep acting and acting, make different attempts to obtain any new information from the text of the problem, try various versions of your actions in different order, reflect on their outcomes.

6. Reflect on what is the difference between the goal of the problem (an unknown) and what you have achieved.

7. "Convert your “defeat” into a key to a solution " (quoting Viktor Zarezki):

- Analyse the reasons for your previous activities, think about why have you been acting like you have been acting (what has forced you to act in that way – your assumptions, your beliefs).

The reason for errors were made or for you got stuck lies either in an inaccuracy of your premises, or in their insufficiency (you have made a mistake at some step or you do not have all the necessary information).

- Formulate the new question to the problem, the answer to which could allow you to make a new step in a solution of the problem.

- Locate/state the areas/topics for the search to find the answer to the new question, formulate methods for searching the answer to the new question.

- Search and find the answer to the new question, state what additional information do you have now.

- State what new steps could have been used now (with this new information), establish the new sequence of steps which could lead to the solution (basically, this is your hypothesis on a method for creating a solution of the problem).

- Check your hypothesis, proceed, try your new approach.

- Get the result, if not there yet, ask yourself the following of questions: Am I really want to solve this problem, Am I sure of my success, Who can assist me in my work, Am I ready to start, Do I get myself thinking in circles repeating again and again the same steps, Why have I started to do this but not that, Because of what ideas I proceeded my reasoning in this way, How can it be done in a different way, What can I try to do instead of doing this, What can be the obstacle preventing me for solving a problem, What else can be tried out in order to bypass or to remove an obstacle and why is this?

- Get the result, if not there yet, go back to part 6. To help yourself in creating a solution, reread the technique for creating a solution in physics.

II. Technique for creating a solution in physics.

1. Analysis of a situation:

Select (and formulate the reasons for your selection):

- Key objects.

- Main interactions between objects.

- Main processes happening to objects.

- Have you met the similar situation before?

2. Abstractization and schematization:

- Determine main empirical terms (everyday words) used for the description of the physics situation of the problem.

- Make the visual image of the situation (draw a detailed picture).

- Link/connect the empirical terms to appropriate physics concepts (state/locate the appropriate region/area/topic of physics).

3. Translation of a problem into theoretical language:

- Find the correspondence between empirical terms and theoretical terms (“a car” = “an object”, etc.).

- Translate the text of the problem from empirical language into theoretical

4. Determination of a model:

- Select main parameters describing the objects and processes (formulate the reasons for the selection).

- Select key parameters describing a situation as a whole.

- Determine variables for chosen parameters.

- Correlate/compare the chosen variables with the variables for similar physical models.

- Determine classes of the phenomena most relevant to the situation described in the problem.

- Select models the closest to the situation considering the set of variables used to the algebraically description of the key physical parameters/quantities.

5. Mathematical description:

- Establish the correspondence between specific objects, processes, quantities essential to the considered situation and the general (abstract, theoretical) objects, processes, quantities describing the chosen classes of the phenomena and models.

- Establish the set of main categories essential to the description of selected classes of the phenomena and corresponding models.

- State main laws and definitions relevant to classes of the selected phenomena and models.

- Write main algebraic statements/expressions corresponding to the laws and definitions.

6. Solution:

- Substitute the given numbers in the stated equations.

- Perform the mathematical transformations necessary for determination of the values of the quantities.

- Analyze the obtained results from the point of view of their reasonableness, naturalness, consider the possible limiting cases.

III. Logic of creating a solution.

Corresponding to the technique described above, the below is a description of mental operations which have to be realized at each stage of the solution; this part of mental work consists of the answers to the following questions:

1. Analysis of a situation:

- What can we say about objects (bodies, things) in the condition of a problem?

- What is happening to the objects, in what processes are they participating, do they experience any changes, what changes?

- What is influencing the objects, do some objects act on another, are there some interactions, what interactions?

2. Abstractization and schematization:

- What words (usually they are nouns) are used to name the objects/bodies?

- What words (usually they are verbs) are used to describe the processes (what is happening to the objects)?

- What words (usually they are adjectives or adverbs) are used to describe/indicate properties of both bodies and processes?

- How can you visually represent each object and what is happening to it using a picture?

- What theoretical categories/terms a physicist would use to describe the similar objects and processes?

- What is a possible "translation" of the text of the problem into a theoretical language?

3. Determination of the type of a model:

- What are the main physical quantities (terms, categories) used for the description of a situation?

- What physical phenomena can be described by using the same physical quantities (terms, categories)?

- What are the main parameters of classification used to select an appropriate model?

- What are the values of these parameters for your problem?

- What is the name of the physics model(s) which has/have the same values of the same parameters?

4. Mathematical description:

- What are the main physical quantities used for the description of the selected models?

- What of the main physical quantities from above are connected by some physical relations/dependents?

- By what kind of equations are the physical quantities connected?

5. Solution:

- What physical quantities used in the equations which are relevant to the selected model/models?

- Can we select appropriate variables (letters) for the physical quantities using in the model and can we write the equation corresponded to connections between them?

- What numerical values can be substituted in the equations for the labels/letters of the quantities (corresponded variables)?

- How many unknowns and algebraic equations are obtained as the result of the substitution?

- How can we solve the obtained set of equations?

- Do the obtained solutions look reasonable or they contradict to your experience?

IV. Reflection on the process of creating a solution.

- Analyze the process of creating a solution: - about what, in what sequence, for what reason, with what outcome it was necessary to think during creating a solution; what happened during the reasoning; what problems had been overcome; what kind of emotions have been experienced?

- Analyze the solution found: - is the method of creating the solution applicable to only the given problem or it can be generalized for the class of problems; what indicators/parameters determine this class of problems (by using which indicators can a problem be assigned to the given class)?

- State a general method for solving a problem from the given class/set of problems.

The most important part of the mental activity leading to the development of skills needed for creating a solution of a problem is reflecting the own activities performed during the problem solving process. Technically, this part of the activities is carried out by answering to a number of questions pointing to oneself, such as: "Am I really want to solve this problem?", "Am I sure of my success?", "Who can assist me in my work?" , “Am I ready to start?", "Do I get myself thinking in circles doing again and again the same steps?", and etc..

All textbooks start solutions from writing down the necessary equations, which then get applied to solve the problem. When reading this approach for solving a problem, students do not know how did the author know what kind of equations to choose? In reality, writing down the necessary equations is the final step of analysis! Physics is done after that! Math is starting. The main cause for misunderstanding Physics and for inability to solve Physics problems is the lack of experience of making the analysis which leads to the necessary equations! This is the focus, the main goal and the most valuable result of Physics education.

The described “algorithm” introduces one of the most interesting problems of creating new efficient educational tools, which belongs to psychology, neurology and educational science.

Any algorithm, like any written or spoken text, has a sequence of words (or symbols), which connected to each other in a specific way, mostly linear (like the text you are reading right now). But a brain analyses a huge amount of signals simultaneously, a brain does not work linearly, it works making at the same time a lot of “parallel calculations” (like a computer with a lot of processors working in parallel). The structure of the information translated to students does not correspond to the structure of the information a brain used to deal with. Hence there must be a certain/specific process a brain is using for transforming one kind of the structure into another. The effectiveness of this kind of transformation has to have a direct influence on the effectiveness of mastering a subject. Usually this process happens in a natural way without a purposed influence from a teacher. I believe, if a teacher could effectively help a brain to make a transformation between different types of structuring information a brain is processing, it would lead to better learning outcomes of students (and it would require new approaches for constructing educational tools and organizing lessons). The presented “algorithm” is one of the instruments a teacher can use when helping a brain of a student with organizing its (brain’s) work.

“What can’t be measured - can’t be managed”. This sentiment is widely accepted by the members of a financial and business community. In education, however, the discussion of “accountability”, and “measurability” brings many controversial views and opinions on absolutely all levels. What should not and what should be measured, when, by whom, what conclusions and decisions should be derived from the results?

But the most controversial question is “how”? Currently there is no tool for measuring learning outcomes of students, which would be broadly accepted by teachers, schools and district officials, by parents, policymakers. An open to public, consistent with the learned content, and uniform by the procedure and results tool for measuring learning outcomes does not exist. The situation is like all 50 states had different currency, and there were no exchange rates, there was no way to use money from one state in another one.

As the consequence, any data on the quality of teaching are always readily adopted by one “camp” and vigorously disputed by another one (the latest example is represented in The Boston Globe, on March 19, 2015, in article “Boston’s charter schools show striking gains”).

As a physics teacher I am concerned with having a reliable tool for measuring learning outcomes of students taking physics courses. I firmly believe all teachers should be concerned with the methods and techniques used to measure learning outcomes of their students. The method described below had been developed for measuring learning outcomes of students taking physics course, but the methodology can be applied to other subjects as well, and I am inviting teachers to use that methodology and develop their own measuring instruments.

Many instruments to measure learning outcomes in physics have been proposed and used, including but not limited to: the Force Concept Inventory (Hestenes et al.), the Force and Motion Conceptual Evaluation (Thornton, Sokoloff), the Brief Electricity and Magnetism Assessment (Ding et al.), SAT physics subject test, AP physics exam, MCAT (physics questions). However, all current tools for measuring learning outcomes suffer from at least one, or several deficiencies listed below:

1. the list of concepts depends on the preference of a developer and usually not open to a user (one using an inventory can derive an assumption about the concepts analyzing the questions in the inventory, but that is only an assumption).

2. The set of questions depends on the preference of a developer.

3. The set of questions is limited and cannot be used to extract gradable information on student’s skills and knowledge.

4. The fundamental principles used for development of a measuring tool are not clear or not open to public, teachers, instructors, professionals.

5. The set of questions becomes available for public examination only after being used, hence it only reflects the view of the developers on what students should know and be able to do, there is no general consensus among the users, instructors, and developers on what should be measured and how to interpret the results.

6. The set of questions change after each examination, which makes impossible to compare the results of students taking different tests (public should just rely on the assertion of the developers that the exams are equivalent, having no evidence of that).

I certain that a tool and a procedure used to measure learning outcomes of students taking physics course (or, for that matter, any STEM course) must satisfy the following conditions:

(a) Every aspect of the development and the use of the tool has to be open to public and be able to be examined by anyone.

(b) The use of the tool must lead to gradable information on student’s skills and knowledge.

It might seem impossible to develop a tool, which would satisfy all the conditions above. However, in fact, there is a singular example of the use of a tool like that: without a solid theoretical foundation, but rather as a practical instrument a similar tool for measuring learning outcomes of prospective students had been used at Perm Polytechnic Institute (Russia, ~ 1994 - 2003).

The methodology for development of the tool is based on a “driving exam” approach, which requires - instead of a verbal description of skills and knowledge a student has to display after taking a course (a.c.a. “standards”) – a collection of exercises and actions for which a student has to demonstrate the ability to perform (assuming the full level of learning).

The methodology is based on the following three principles.

1. In physics every component of student’s physics knowledge or a skill can be probed by offering to a student to solve a specific problem.

2. For a given level of learning physics there is a set of problems, which can be used to probe student’s knowledge and skills.

3. For a given level of learning physics a set of problems, which can be used to probe student’s knowledge and skills, has a finite number of items.

Hence, it is plausible to assume that to test the level of acquired physics knowledge and skills a collection of problems can be developed which - when solved in full - would demonstrate the top level of achievement in learning physics (an A level of skills and knowledge). A subset of a reasonable size composed from problems selected from the set can be used as a test/exam, which can be offered to a student to collect gradable information on student’s skills and knowledge.

In early ninetieths in Perm Polytechnic Institute a set of about 3000 problems had been developed and used to compose an exam constituted of 20 problems with different difficulty level to be offered to high school graduates applied to become PPI undergraduates.

The philosophy behind the approach was simple: it is just impossible to memorize the solutions to all problems in the book (a book was openly sold via PPI book store), and even if there was the one who could memorize all the solutions, PPI would definitely wanted to have this person as a student (FYI, the competition to become a PPI undergraduate was fierce).

The path to the theoretical foundation of the describe approach had been laid out by me in my work in 1996 – 1998.

Below is a summary of the publications (my translation from Russian) related to the project.

There are three fundamental principles which represent the theoretical basis of the work.

The first principle states that all physics problems can be classified by (a) the set of physics quantities which have to be used to solve a problem;

(b) the set of mathematical expressions (which by their nature are either definitions or laws of physics, or derived from them) which have to be used to solve a problem; and (c) the sequence of the steps which have to be acted in order to solve a problem (an example of a general “algorithm” for solving any physics problem is at http://teachology.xyz/general_algorithm.htm).

The second principle states the importance of the new terminology needed to describe and classify different problems (in physics many similar problems use very different wording). All problems which can be solved by applying the exactly same set of quantities (a) and expressions (b) and the same sequence are congruent to each other. Problems which use the same sets (a) and (b) but differ by sequence (c) are analogous problems. Two problems for which set of physics quantities (a) differ by one quantity are similar. Four problems below are offered to illustrate the terminology. Among three problems below problem A is analogous to problem B, and congruent to problem C. Problem D is similar to problems A, B, and C.

Problem A. For a takeoff a plain needs to reach speed of 100 m/s. The engines provide acceleration of 8.33 m/s2. Find the time it takes for the plain to reach the speed.

Problem B. For a takeoff a plain needs to reach speed of 100 m/s. It takes 12 s for the plain to reach this speed. Find acceleration of the plain during its running on the ground.

Problem C. A car starts from rest and reaches the speed of 18 m/s, moving with the constant acceleration of 6 m/s2. Find the time it takes for the car to reach the speed.

Problem D. For a takeoff a plain needs to reach speed of 100 m/s. The engines provide acceleration of 8.33 m/s2. Find the distance it travels before reaching the speed.

It is important to stress, that all congruent problems can be stated using a general language not depending on the actual situation described in a problem.

Problem E below is congruent to problems A and C and stated in the most general language not connected to any specific situation.

Problem E. An object starts moving from rest keeping constant acceleration. How much time does it need to reach a given speed?

The third principle states that for every problem a unique visual representation can be assign to it, which reflects the general structure of the connections within the problem. This visual representation is a graph (an entity of a graph theory): each node (vertex) of the graph represents a physical quantity without the explicit use of which a problem cannot be solved; each edge of the graph represents the presence of a specific equation which includes both quantities connected by the edge (link).

Each graph represents a specific example of a knowledge mapping, but has to obey to two strict conditions (which makes each graph unique and this approach novel):

1. every quantity represented by a vertex/node of a graph must have a numerical representation, i.e. has to be measurable (capable of being measured).

2. every edge (link) between any to vertices must have an operational representation: i.e. for any quantity represented by a vertex, if its value is getting changed, and the values of all but one other quantities represented by other vertices connected to the changing one are being kept constant, the quantity represented by the remaining vertex linked to the changing one must change its value.

Graphs, which satisfy the above two conditions, represent a novel technique to represent specific scientific content (I call it “a map of operationally connected categories”: MOCC).

Knowledge maps usually represent the thought process of an expert in a field solving a particular problem (analyzing a particular situation). MOCCs represent objective connections between physical quantities, which imposed by the laws of nature.

The second condition eliminates possible indirect connections/links (otherwise the structure of a graph would not be fixed by the structure of the problem, but would depend on the preferences of a person drawing the graph). However, even in this cases there is a room for a discussion: should the links/edges represent only definitions and fundamental laws or also expressions derived from them? This question should be answered during the trial use of the developed tool.

All problems which graphs include exactly same set of quantities (a) are called like problems (they compose a set of like problems). A problem which is stated in a general language and which is like to all problems in a set of like problems is the root problem of the set (any specific problem in a set can be seen as a variation of the root problem). The project is based on a proposition that a set of root problems can be used to describe desired level of learning outcomes of students.

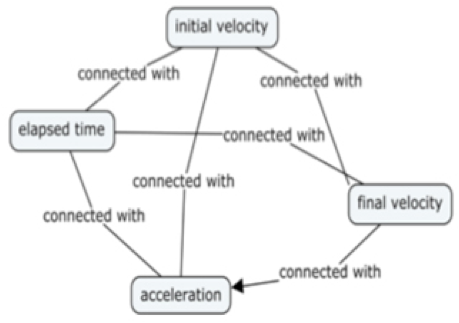
One of the consequences of the graphical representation of a problem is the ability to assign to it an objective numerical indicator of its difficulty D = NV + NE, which is equal to the sum of the number of vertices included in the graph NV and the number of unique equations represented by the edges of the graph NE. This indicator can be used for ranking problems by their difficulty when composing a specific test to be offered to a student. This indicator of difficulty does not depend on a perception of a person composing a test and provides uniformity in composing tests (this is the simplest of the objective indicators of difficulty of a physics problem which are based on the topology of MOCC corresponded to the problem).

For example: every specific problem congruent to problem E corresponds to the graph on the right with difficulty D = 5 (four quantities and one equation which relates them).

Each link of the graph on the right represents the same connection/equation:

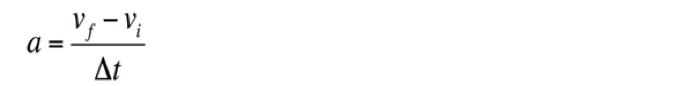
(the graph was drawn using CmapTools: http://cmap.ihmc.us/)

I am positive that MOCCs represent the best instrument for classification of physics problems and developing a tool for objective measuring learning outcomes of students taking physics courses.

The same principle also can be used for developing an analogues tool for measuring learning outcomes of student taking any STEM course.

In math, and chemistry to assess learning outcomes of students all we need to do is – as we do it in physics – to offer them to solve several problems – theoretical (“calculate the landing speed of a ball released from rest 5 m above the ground”, “find a hypotenuse of the given right triangle”, “finish the chemical reaction”) or experimental (“measure the critical coefficient of static friction”, “find the value of number ?”, “use following chemicals and extract hydrogen gas”); some people may like to add some specific theoretical questions (“what is the definition of average velocity?”, “state the Newton’s second law”, “state the Pythagorean theorem”, “What is an endothermic reaction?”).

The good thing about questions and problems in STEM subjects is that the number of such questions and problems which could be used for assessing learning outcomes is finite! Of course, one can invent infinitely many wordings/versions for the same problem, which may look differently, but the underlining thinking process for the development of the solution for all those problems would be the same (“congruent problems”).

The collection of all truly different problems (not “congruent” to each other), which are sufficient to measure the level of learning, is limited. In math, for example, instead of describing what skills students should demonstrate by the end of the 7th grade, one could generate an exam using items from a book of all problems and questions students should be able to solve and answer at the end of the 7th grade (to get an A, to get an A-, etc.).

Note, please, that the book would be the same for all teachers teaching 7th grade math, but the exams used by different institutions could have been different – but comparable (!).

Literature for additional reading:

Edward F. Redish, “A Theoretical Framework for Physics Education Research: Modeling Student Thinking”, http://arxiv.org/abs/physics/0411149.

Arnold B. Arons, “Teaching Introductory Physics”, Wiley, 1997.

K. Heller, P. Heller, "The Competent Problem Solver, A Strategy for Solving Problems in Physics", McGraw-Hill, 1995.

A. Elby, “Helping physics students learn how to learn”, American Journal of Physics, Physics Education Research Supplement, 69(7), S54-S64 (http://www2.physics.umd.edu/~elby/papers/epist1/epist_curric.htm).

David Rosengrant, Alan Van Heuvelen, and Eugenia Etkina, “Do students use and understand free-body diagrams?”, Phys. Rev. Special Topics – PER 5, 010108, 2009.

D. Van Domelen, “Problem-Solving Strategies: Mapping and Prescriptive Methods”, http://www.eyrie.org/~dvandom/Edu/thesis.html

Lillian C. McDermott and Edward F. Redish, Resource Letter: PER-1: Physics Education Research, Am. J. Phys. 67, 755 (1999).

Joseph D. Novak, D. Bob Gowin, Jane Kahle, “Learning How to Learn”, Cambridge University Press, 1984.Thornton R.K., Sokoloff D.R. (1998) Assessing student learning of Newton's laws: The Force and Motion Conceptual Evaluation and Evaluation of Active Learning Laboratory and Lecture Curricula. . Amer J Physics 66: 338-352.

Hallouin I. A., & Hestenes D. Common sense concepts about motion (1985). American Journal of Physics, 53, 1043-1055

Hestenes D., Wells M., Swackhamer G. 1992 Force concept inventory. The Physics Teacher 30: 141-166.

Hestenes D., 1998. Am. J. Phys. 66:465

Ding L., Chabay R., Sherwood B., & Beichner R. (2006). Evaluating an electricity and magnetism assessment tool: Brief Electricity and Magnetism Assessment (BEMA). Phys. Rev. ST Physics Ed. Research 2

Voroshilov V., “Universal Algorithm for Solving School Problems in Physics” // in the book "Problems in Applied Mathematics and Mechanics". - Perm, Russia, 1998. - p. 57.

Voroshilov V., “Application of Operationally-Interconnect Categories for Diagnosing the Level of Students' Understanding of Physics” // in the book “Artificial Intelligence in Education”, part 1. - Kazan, Russia, 1996. - p. 56.

Voroshilov V., “Quantitative Measures of the Learning Difficulty of Physics Problems” // in the book “Problems of Education, Scientific and Technical Development and Economy of Ural Region”. - Berezniki, Russia, 1996. - p. 85.

Chapter 11: Learning aides for students taking physics.

In the previous Chapter I described a map of operationally connected categories (MOCC) as an instrument for classifying physics problems (http://teachology.xyz/mocc.htm).

In my teaching experience, MOCCs also proved to be a helpful teaching instrument/learning aid.

One of the use of MOCCs is having it drawn for a problem being solved in front of a class. The visualization of logical connections between quantities helps students to grasp the logic of creating of the solution. Some students develop a habit of using MOCC when study physics. MOCC also can be used as an end of a topic assignment, when students should use it to visualize all the important connections they have learned. Below you see an example of such a MOCC developed by a student after topic “Direct Electric Current”.

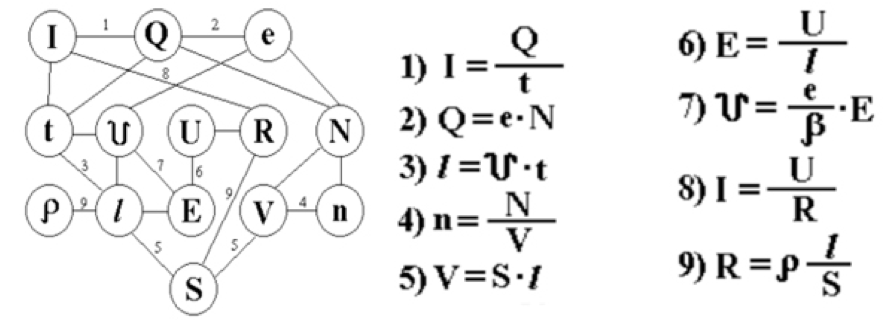
In the diagram and equations above for the most of physical quantities we assume a common variable representation, except V (here - volume), and U (here - voltage).

The pedagogical use of MOCCs is more efficient if combined with the use of other learning aids. All of the learning aids described below can be used for developing similar aids (i.e. aids based on similar principles) for students taking other than physics courses.

(I) A physicist always compares a given problem against a set of previously known situations (models), and to do that he or she uses a certain classification (usually on a subconscious level).

A teacher can show students this kind of mental work as a part of the problem solving process.

Any process of recognition is always based on some classification parameters and their values. For example, in elementary Kinematics, to identify the model we deal with two main parameters of classification: 1. The form of the trajectory; 2. The behavior of the speed. Within the standard framework, the following values of the parameters are important:

The form of the trajectory: The behavior of

the speed:

a) STRAIHGT LINE; a) DOES NOT

VARY (constant);

b) CIRCLE; b) VARIES

(changes).

In relation to the values of the parameters, four main kinematics models can be identified.

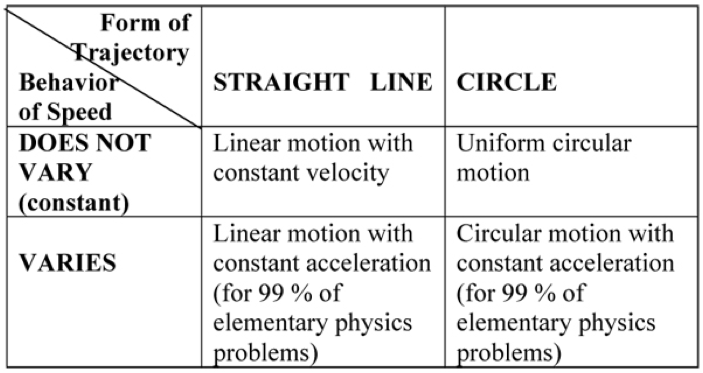
We cannot use the table to solve any problem on Kinematics, but we can use the principle!

(II) When the model is identified; then we can assemble a set of the most important physical quantities needed to investigate the model, for example as shown in the table an the next page (these are the physical quantities which are most probably involved in solving a problem on Kinematics).

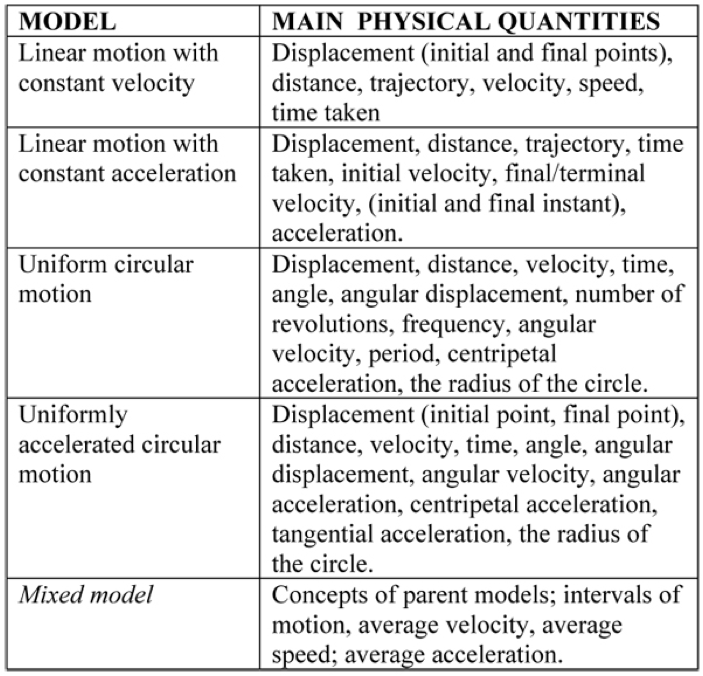
(III) Finally, we can write equations which (most probably) will be useful for solving a problem. For example, the table below represents the correspondence between the kinematical models and the formulae which can be used for them.

It is important to emphasize that this step – choosing equations – is usually the last step of the analysis of the problem (when done by an expert). After this step physics is done, merely mathematical calculations are left.

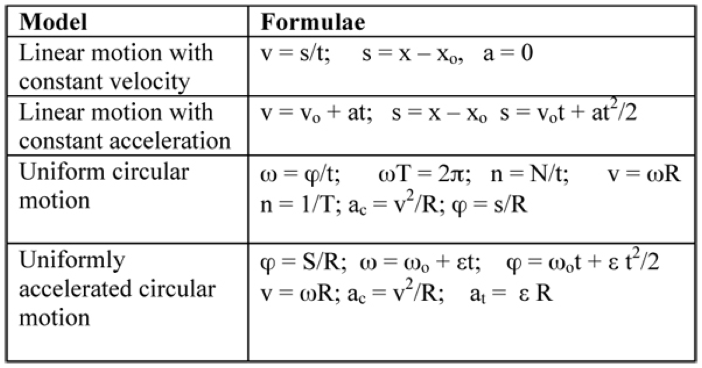
(IV) When a physicist reads a problem he/she translates it immediately (and intuitively) into the text written using a general language.

For example, a problem “For a takeoff a plain needs to reach speed of 100 m/s. The engines provide acceleration of 8.33 m/s2. Find the time it takes for the plain to reach the speed.” will be translated as: “A body moves from rest with a constant acceleration (which is given) and at some instant of time (which is unknown) has a specific speed (which is given).”

A special tool – “a dictionary” – will help students to conduct this kind of translation. An example of such “a dictionary” is on the next page.

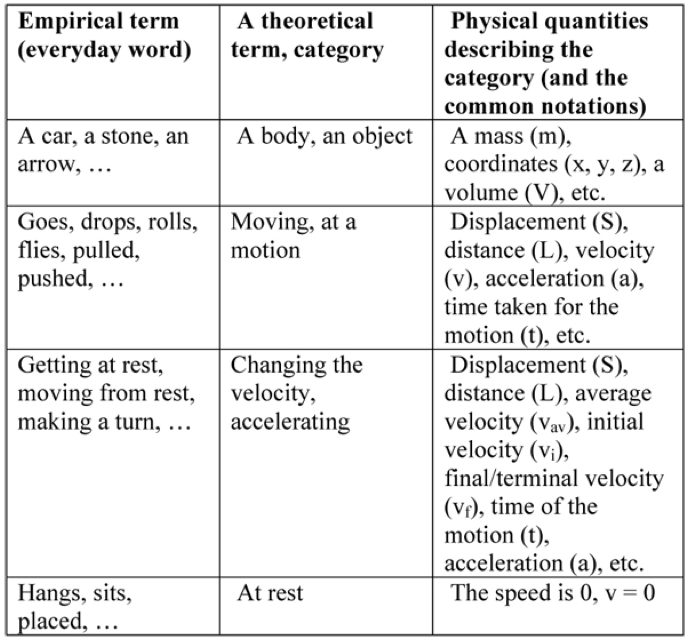
All the learning aids (a.c.a. teaching tools) describe above can be used as a part of the toolbox for measuring learning outcomes of students taking physics course: students can be offered identify a model, translate a problem, draw a MOCC for the given problem, to follow a general algorithm for solving physics problems. I believe, the principles used for developing the tools can be used for developing similar teaching tools/ learning aids in different subjects. I think an experienced teacher should be able to develop similar or even more advanced tools for his or her students.

Chapter 12: Math self-test for science teachers (and teachers students planning on taking physics course).

Back in a day, when I was just starting my teaching career, I had been tutoring a lot - dozens of hours a week. Tutoring is an indispensible tool for a teacher to get deep understanding of how people think (tutoring, if done correctly, is basically a clinical study). My ultimate goal always was to guide a student to n answer, and only if it would have taken too much time I would gave the answer away. Eventually, after one or to meetings with a new student I could “predict” either what would be the maximum grade the student get in a class, or how much time would we need to training the student to an A (or A-, but if that did not seem possible for me, I would find some words to express my concerns or doubts).

When I started teaching college physics, I quickly came to a conclusion that the final grade of a student is heavily based (among other things) on his or her math background. I could not asses logical abilities or cultural background, but I have developed a short mat test which I offer to my students as a self-assessment (FYI: wouldn’t it be awesome to have students take a quick test and tell them “which your current background the maximum grade you can get is B-; if you want a better grade this is what you need to do”).

Study physics without solving problems is like learning how to play tennis without ever using rackets. To solve physics problem the use of some level of math is inevitable and unavoidable. If a student spends on the test about an hour and solves about 85 % of problems, that student should not have any problems with getting an A for the course. Otherwise, a student needs to address as quick as possible some of topics from math class.

I also believe that every science teacher should be able to do this test quickly and in full.

And I also think an experienced teacher should be able to develop a similar test for students taking his or her class.

The instructions to the self- test are self-explanatory.

Test your math background

Below you find a set of different mathematical problems. Try to solve as many as possible. The math skills required to solve the problems are important for taking any algebra based Physics course. When solving the problems try using your calculator as least as possible. If you are not sure how to solve a problem – that is something to work on before taking Physics (although during the course I will provide the examples of the solutions to similar problems). Good luck!

Here is some information from trigonometry commonly used for solving physics problems.

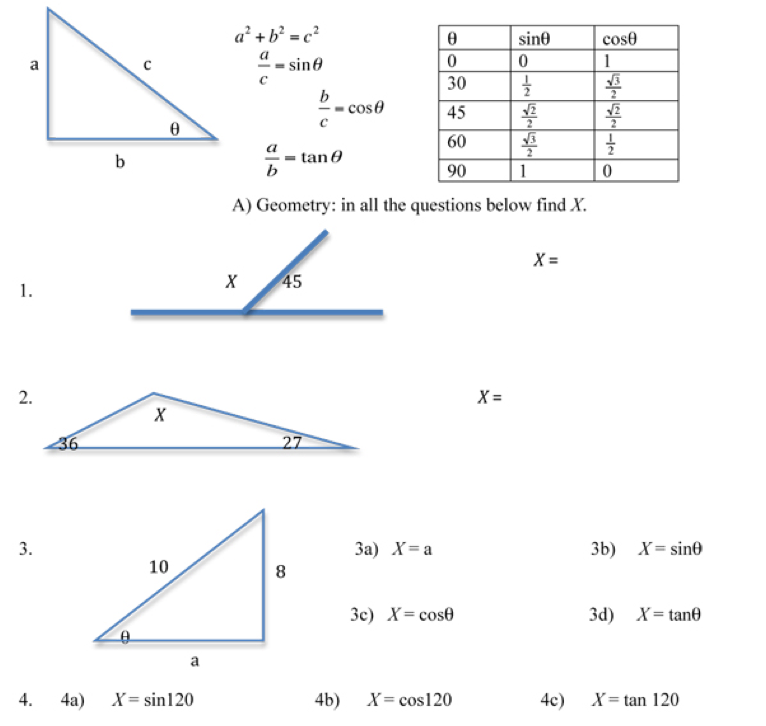
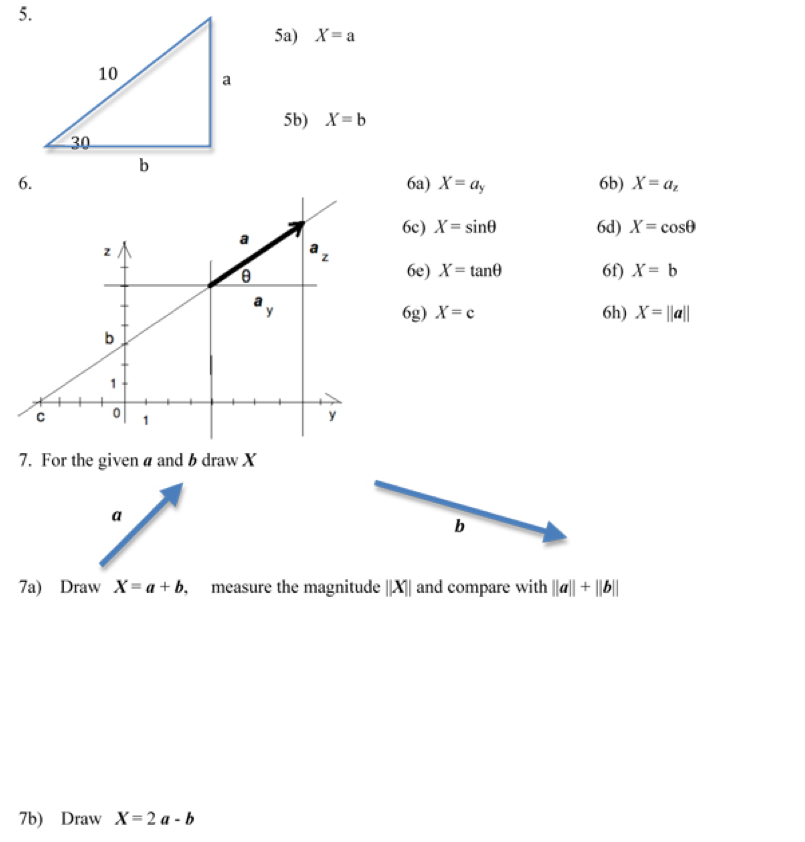
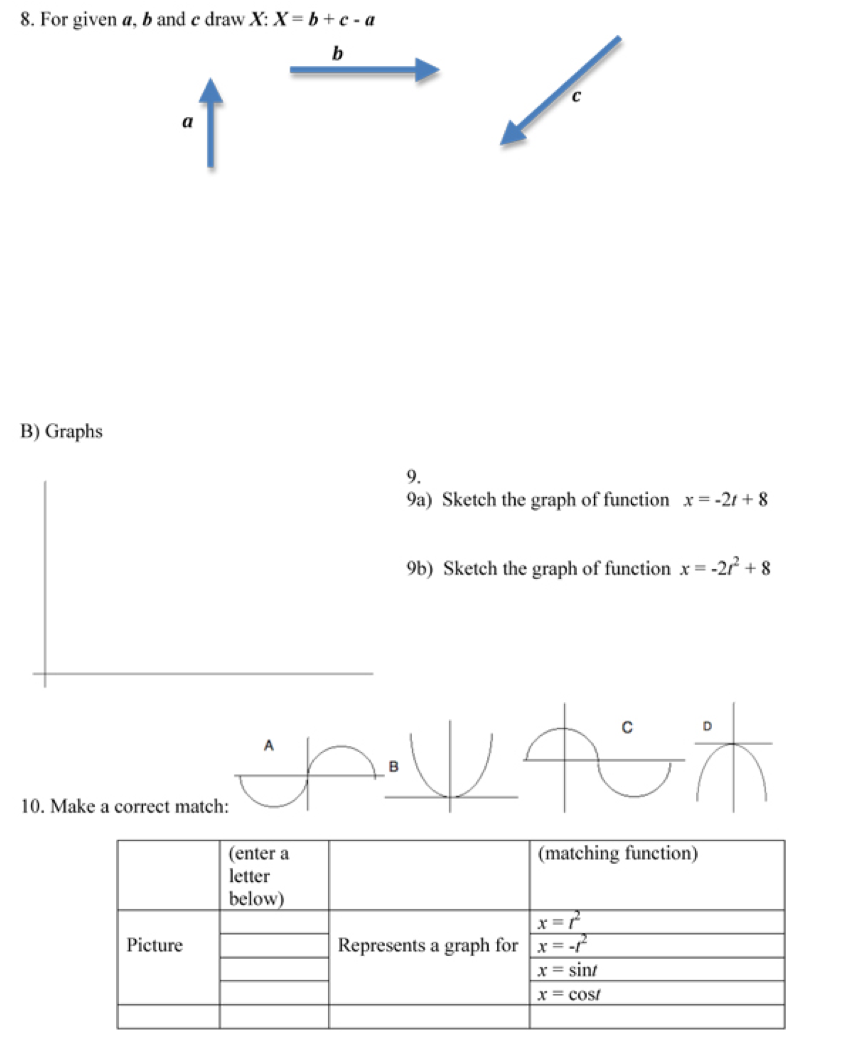
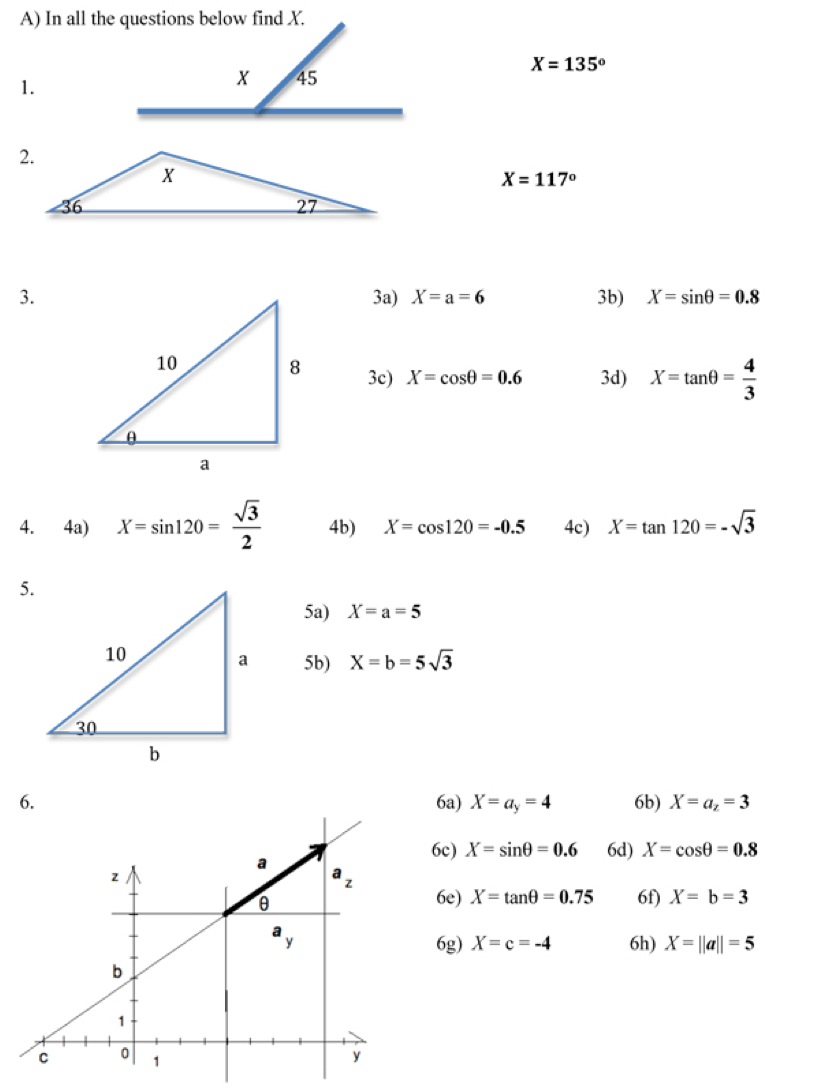
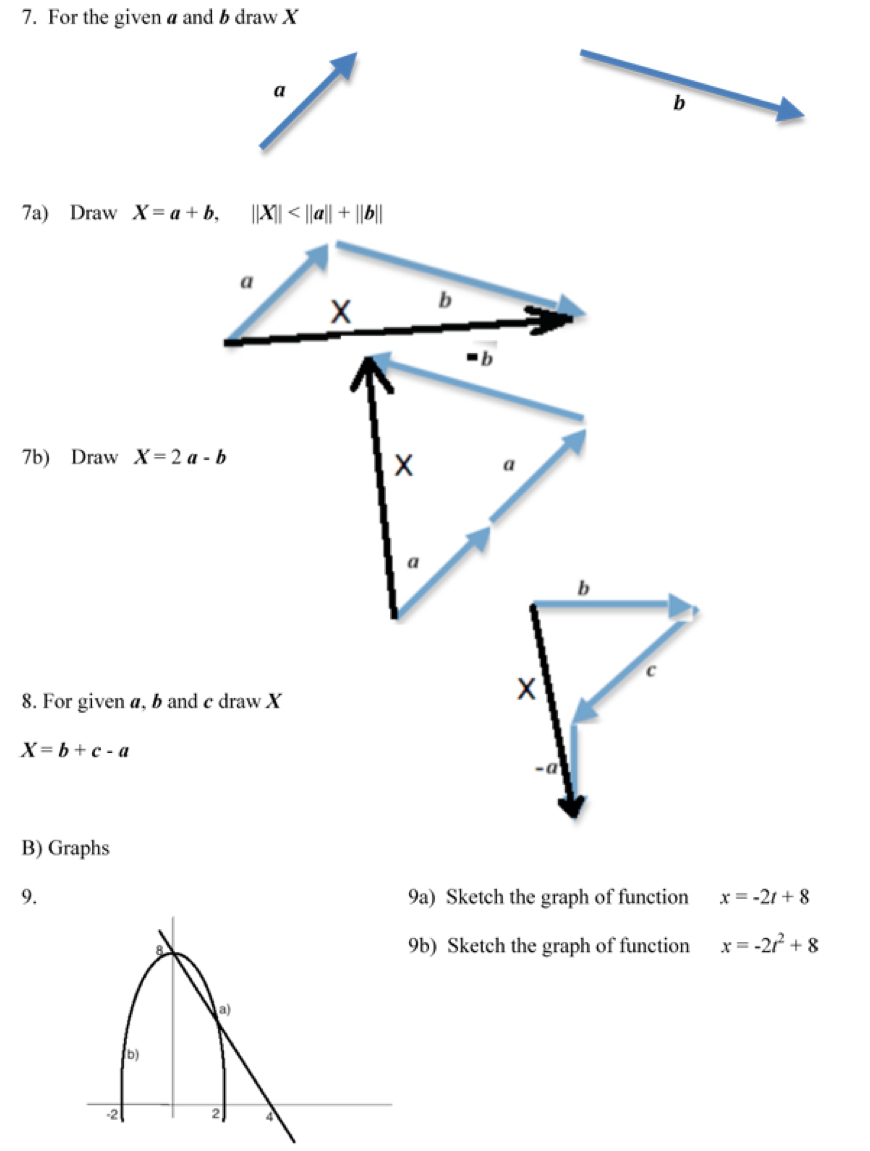
Chapter 13: Critical reading of “Making sense of confusion” by Jason E. Dowd, Ives Araujo, and Eric Mazur1

Reading what people think about teaching is an important part of being a professional educator. The main goal of such a reading should be solidifying the personal views on teaching and learning by compering them to what written by other educators. A teacher needs to keep in mind that not every paper published in a science journal represents results of a solid scientific study. Since Teachology is only in its infancy as a science, there are many papers which have internal inconsistencies or logical flaws.

For example, I had to write a review on a draft of a paper about how teachers percept different diagrams. The question presented as a research question of the study was: “To see if science teachers and non-science teachers would describe diagrams differently”. Different diagrams (with no criteria presented why they had been selected and others not) had been offered to different teachers. In the end the authors concluded that “all teachers could not describe diagrams at the same level as an expert physicist could”. The conclusion is clearly inconsistent with the study question (there is an easy fix, though; the authors could have studies “the differences between diagram description provided by teachers and an expert”).

Another example, which might be of an interest for a physics teacher, is a paper “Some Consequences of Prompting Novice Physics Students to Construct Force Diagrams” by Andrew F. Heckler (International Journal of Science Education; 2010). After reading a 21 pages paper we learn that 891 students had to solve some problems; some of the students had a prompt “use a force diagram”, and others did not have it. For a teacher, the paper provides a very strong motivation to think about how diagrams may help students to solve problems, and also is a very good source for further reading on the topic. However, this paper does not provide a logical “cause and effect” relation, as a science paper should. Students’ ways of solving problems is influenced the most by instructions and problem solving examples provided during the instructions.

From the paper we can only learn that some students were taking a “typical” physics course, and others were taking an “honors-leveled” course.

The authors assume this description is clear enough, but in reality, a name or a type of a course has no correlation with the actual instructional techniques. In particular, we do not know if some of the students had been exposed to a problem similar to the one offered during the experiment; we do not know how similar or how different (and for how many students) the offered problems were comparing to the ones solved during taking a course. Hence, such strong factor as “similarity” had not been taking into an account, and the study cannot be used for making any scientific or practical predictions.

It is very common for people (especially for teachers) to feel awe when meeting a university professor, a scientist. “This guy is so smart, the guy has a PhD for God’s sake”.

Yes, it is true, but it does not mean one has to believe everything a scientist say, especially if the one is a teacher and the scientist talks about teaching.

A short example above is to demonstrate that if a paper has been published in a journal, it does not mean we should just accept everything said in it.

Things to keep in mind.

1. An experienced teacher might not sound as eloquent as a scientist but may know much more about teaching, especially if the scientist has no real teaching experience at a middle or high school level. When I listen to a speaker, the first question I have is what is his/her teaching experience (to me it means that the speaker knows or not what he or she is talking about).

2. We should admire science, but also should keep in mind that doing science requires basically advanced reading and writing skills – and anyone (if healthy and have time) can do what 99.99 % of scientist do (0.01 % falls on such geniuses as Newton, Einstein, and others). Ordinary people like you and I are capable of getting PhD, as long we put enough effort and time in the work (unfortunately, no everyone has such luxury as time which can be spent of learning).

3. A science is like a religion – a finite number of words put in sentences, often supplied by symbols, pictures, and (for a quantitative science) by sets of numbers, graphs, equations. From a descriptive point of view, there is no difference between a religion and a science: both have postulates (statements which cannot be proved and people just believe in them because of some reasons), both have statements logically derived from other statements (this logic might also be of a mathematical nature). The difference is not between a science and a religion, but between a scientist and a religious person.

A scientist accepts a possibility of his or her believes (postulates) to be overturned (proved to be wrong, or limited), and a scientist is open to a discussion about his or her believes. A religious person cannot accept a possibility of his or her postulates to be limited, wrong, overturned; a religious person will just deny any other postulates or statements if they contradict his or her believes. Hence, when listening to a scientist, a teacher should try to infer information on his of her believes, and (a) to compare with teacher’s own believes (nothing good could come out of a forced collaboration if people have very contradictory believes), (b) to confront some of the postulates a scientist uses as building blocks for his or her theory of teaching (a true scientist is never afraid of such confrontation, and a teacher should not spend time on communication with a “not-true” scientist).

FYI: of course there is an important difference between a religion and a science; they have different goals. A religion is about morality, social norms, what is right and wrong to do (that is why there are many religions), A science is about truth; about a correct description of the world (that is why there is only one physics, chemistry, etc.).

4. A teacher should read at least a couple of scientific papers a year (the best would be having a subscription to a magazine). However, when reading scientific papers a teacher should critically analyze each premise, each conclusion, and most of all, if this work can be of any use for a teacher. Writing a short critical essay on a paper which just had been read is also a good experience and useful practice.

Recently I had read a paper in Physics Review Letters written by a well know scientist. I did not like it. I published my detailed critical analysis of the paper2. I would recommend everyone to read the original paper and then my work and provide a critique for both (this helps to advance our critical thinking skills and also to strengthen a personal view on what research in education should be about).

Below is my original paper.

The scientific method developed to study physical phenomena presents a proven instrument for conducting research in any other field of science. Yet, vast amount of literature on physics education research does not represent examples of application of that scientific method, even if the researchers are physicists. In this paper the author offers a critical reading of one of recent papers published by Physical Review Letters. The goal of this work is to stimulate a conversation on how the scientific method developed to study physical phenomena can be applied to study phenomena in realm of education.

Physics represents a perfect example of how the scientific method should be applied to study, well, everything.

At first a scientist observes, collects facts, develops vocabulary, classifies objects and processes, tests some preliminary ideas, but in the end the scientist formulates postulates (a.c.a. axioms, or laws). It usually is impossible to test the postulates by direct measurements; the consequences derived/predicted from the laws, however, can and should be tested, and while the experiments agree with the predictions, we believe in the correctness of the postulates, we keep using the theory.

Of course, every theory has limits, hence when experiments contradict the theory, a scientists starts thinking, is it something wrong with the experiments, or the limits of the theory finally have been reached?

The Newtonian Mechanics, the Maxwell’s theory of electromagnetic phenomena, the Einstein’s theory of Special Relativity, the Einstein’s General Theory Relativity, the Euclidian Geometry are some of the bests and clearest examples of such approach.

Can the same approach be applied outside of physics, say, to study learning and teaching phenomena? The answer to this question depends on a personal view.

In 2002 Richard Hake wrote2: (begin the quote) “There has been a long-standing debate over whether education research can or should be "scientific" (e.g., pro: Dewey 1929, 1966, Anderson et al. 1998, Bunge 2000, Redish 1999, Mayer 2000, 2001, Phillips and Burbules 2000, Phillips 2000; con: Lincoln and Guba 1985, Schön 1995, Eisner 1997, Lagemann 2000). In my opinion, substantive education research must be "scientific" in the sense indicated below. My biased prediction (Hake 2000a) is that, for physics education research, and possibly even education research generally: (a) the bloody "paradigm wars" (Gage 1989) of education research will have ceased by the year 2009 (italic by Valentin Voroshilov), with, in Gage's words, a "productive rapprochement of the paradigms," (b) some will follow paths of pragmatism or Popper's "piecemeal social engineering" to this paradigm peace, as suggested by Gage, but (c) most will enter onto this "sunlit plain" from the path marked "scientific method" as practiced by most research scientists” (end of quote).

Thirteen years later this prediction looks overly optimistic.

In many papers, even written by scientists who have been using the scientific method in their field, the authors do not seem applying the same way of reasoning when writing a paper on education.

At the least, that indicates the fact that the authors do not believe that the same scientific method applied to study physics (chemistry, mathematics) should be applied to study education. At the most, that indicates the fact that the authors do not believe that the same scientific method applied to study physics (chemistry, mathematics) can be applied to study education.

For example, let us read the latest publication by Eric Mazur1 and his colleagues.

The main statement I want to make after reading the article is that the methodology (which we call “a scientific method”) which had been developed and being used to study physical phenomena can and should be used for conducting research like the one described in the paper, but the paper does not show the use of that methodology.

Below I will try to support this statement by analyzing the study described in the paper. Clearly, my analysis of the study is based on certain assumptions I made during the reading.

The first assumption is that one of the goals of the study was to find a correlation between: (a) the fact that students are offered to answer questions designed to generate confusion, and assess how confused they are: and (b) learning outcomes. This assumption is based, in part, on the statement: “We ask the following question: To what extent are course performance, … related to confusion?”.

I argue, that if one wants to study such a correlation, one can (and should) use the same methodology which had been developed and being used to study physical phenomena. In the latter approach, one has to compare two (at least) study cases: “Case 1” is when students do not have to answer questions designed to generate confusion and do not have to assess how confused they are; “Case 2” when students have to answer questions designed to generate confusion, and have to assess how confused they are (the “confusion” element becomes a part of a learning experience).

The scientific method also demands that the “Cases” should not be different from each other by anything else but the “confusion” element, which means: student body in both “Cases” should be similar by the number of students, by the age, race, background distribution (for large classes it is reasonable to assume that these conditions are satisfied), students’ course work should be very similar (except the “confusion” element), faculty involvement should be similar, learning outcomes should be measured by the same measuring. If these conditions are not held the learning outcomes of student might be affected by many uncontrolled parameters and the examined correlation cannot be established.

While reading the paper, however, one cannot find any indication on how the introduction of the “confusion” element to some students influenced their learning outcomes, compared with students for whom the “confusion” element has not been a part of the learning process. It is not clear either the authors did not use the scientific method on purpose, or used it but the paper does not provide a clear description of doing that (the further analysis indicates that the former is more probable than the latter).

The presence of this ambiguity in the description of the study makes the study scientifically deficient (I consider an ambiguity of a scientific study as a deficiency). Many similar studies experience a similar deficiency.

It might have helped for a reader to navigate through a paper if at the beginning of the paper the authors would clearly state if they meant using the scientific method (the one developed to study physics), or they did not mean to use the scientific method on purpose.

Another deficiency of the paper (as well as many other similar publications) is the fact that the use of the scientific method would have eliminated the need for spending time and effort on collecting data which, when scrutinized, do not really support or contradict the hypothesis of a study.

Instead, the conclusions of a study could have been derived from a set of well-established facts, a.c.a “postulates” or laws.

Below I provide several illustrations to the statement made above.

Setting the terminology aside, the introduction of the paper tells us that: (a) sometimes students get confused (and we know about that because students express their confusion in words or in actions); (b) students often have their own opinion on how good or how bad they can be when doing physics in general or when solving a specific problem; (c) helping students to reflect on their own thoughts, actions, and feelings may help them to perform better.

To this point we see a complete agreement with everyone’s teaching experience.

(a) Every teacher knows that students ask questions; what to do about it and how to manage each question (or how to initiate questioning from students who never talk) is a different conversation.

(b) The fact that different students may have different thoughts about themselves (in the variety of contexts) is also an everyday experience of every teacher (and again, we will not discuss in this paper what the best strategy is for a teacher teaching a class with students who have different self-perceptions).

(c) The correlation between “help” and “performance” can be derived from a more general principle (which is used use as one of the postulates of the Teachology: a practical science of teaching and learning), i.e. for most people (who do not have extraordinary deviations from average abilities) learning outcomes are directly proportional to the volume and variety of learning experiences (below, the “Postulate”).

For example, a teacher teaches a standard course (lectures, labs, discussions, homework). That leads to certain learning outcomes. If we accept the Postulate, we have to make a conclusion that, if the teacher will make students to do something else (reasonably related to the material) and do it on a regular bases over a long period of time, the teacher can expect learning outcomes to be better.

In particular, making students (in addition to what they would have done before) watching movies, or reading additional texts, or discussing qualitative questions, or making them to reflect on what they read and how they felt will result in better learning outcomes.

One can compare any two teaching strategies by counting the amount of learning activities students will have to perform in each. If the material covered is similar by the topics and the volume, but the use of one strategy results in a visibly larger number of learning activities, that strategy will lead to better learning outcomes.

Ballet trainers, sport coaches, parents use this “rule” every day; people say: “practice makes perfect”, and that works every time as long as the practice provides a sufficient volume and variety of learning experiences.

A question like: “Will it affect learning outcomes if in addition to what students have done in the past they will be forced to do such and such?” does not always represent a research question. If “such and such” is related to the learning material, learning outcomes will be better. If learning outcomes did no improve, hence using “such and such” was the wrong choice, or “such and such” has not been used for a long enough time.

The question a teacher should ask is “how can I make students to do “such and such” in addition to what they already do?” This question, however, is not a research question; this is a practical (i.e. social by its nature) question.

Of course, the teacher assumes that the additional learning experience (“such and such”) will lead to better learning outcomes. But this assumption is an assertion (“I believe in the Postulate”) and not a scientific hypothesis, even if it looks like such (like, the assumption that “if I take this root I arrive home faster” is not a scientific hypothesis).

I do not think that any possible question should be called a hypothesis, and any possible activity which leads to an answer should be called a research (my essay2 provides a broader discussion of the difference between a scientific research and a social project).

A research question could have been stated in the following form: “Will learning outcomes improve if we keep the amount of learning activities and the total time of learning practically the same as in the previous course, but rearrange some activities or replace them with different ones?” Unfortunately, as it has been mentioned above, in many papers, including the one under the discussion, there is no available information, which would allow readers to see the specific procedural (technical) differences between the new and the previous learning processes.

Reading the article, however, indicates that in the study described in the paper students - in addition to their regular learning process - had been doing something else: “students were assigned 22 ... and 21 reading exercises”, “in each assignment, the confusion question was posed before the two content-related questions, followed by a final opportunity to revise the response…”.

The statement that “at least two – and sometimes as many as three or four – researches and instructors reviewed and discussed each content-related question …” also shows that during this particular teaching process students have been treated differently then students not participating in the study (the content-related questions were developed using a higher level of involvement of developers).

Based on what I had read, I made a second assumption, namely, that courses taught during the study described in the paper were different from the courses taught before the study by the use of the "confusion" element. Based on this assumption and on the Postulate stated in part (c) I made a conclusion, that the results of the study should be obvious (i.e. should support the Postulate, or the design of the study should be reexamined). If we accept the Postulate, we should expect that the additional practice will be “positively related to a final grade”. In a sense, this study supports the effectiveness of the Postulate (like a working clock supports the effectiveness of the Newton’s laws).

Next I would like to address briefly one specific statement from the introduction: “One cannot express confusion without engaging in metacognition, which involves knowledge and cognition about cognitive phenomena”.

The purpose of this statement is to begin a discussion about metacognition. It is naturally to expect, however, that a student who can explain reasons for his or her actions “will be more strategic and effective in the educational setting” than a student who can just act without being able to explain why did he or she act the way he or she did. This conclusion is a straightforward consequence from the Postulate formulated above in part (c).

An ability to explain the reasons for his or her actions does not come with a birth; it requires a specific type of practice and, of course, a designated time. Hence two students – one who can and another one who cannot explain the reasons for his or her actions – must differ by the volume and variety of learning experiences.

No surprise that every research “consistently suggests that enhanced metacognition is positively related to learning outcomes”. In the end students’ results had been positive, which agrees with the following quote from the paper: “Specifically within physics, researches observe that adding metacognitive tasks to reading-comprehension exercises results in higher post-test scores when compared to a group of subjects who do not complete the metacognitive tasks”.

This is an example of a statement which often sounds like: “We divided students into two groups, in one group students were instructed to learn “that”, in another group students were not instructed to learn “that”, the result is, students in the first group learned “that”, and students in the second group did not ”.

The statement itself, however, is wrong; one can and very often expresses confusion without engaging in metacognition; expressing confusion in many cases is just an emotional reaction to inability to understand something which a person feels like to be expected from him or her to be understood. Every human being might experience many different states, like hunger, tiredness, angriness, confusion. Saying “I am confused” is no different from saying “I am tired”, “I am angry”, etc. It does not require any metacognition. Although, one could redefine “metacognition” by including in it any statement people make about themselves, however it would water down the sole meaning of this term and would make it useless.

The discussion regarding the effect confusion might have on students’ outcomes leads, basically to a conclusion that sometimes confusions is good and sometimes is not.

Every experienced teacher, of course, will agree with this conclusion. However, the mere fact of expressing confusion should not lead to a large change in learning outcomes because it does not involve any additional mental work. The outcome depends on what work has been done to reduce that confusion. An interesting research question is what type of work (step by step guiding, giving away an answer, initiating peer-to-peer conversation, etc.) and under what circumstances would be the most efficient way to decrease or “eliminate” that particular confusion.

The technical realization of the study has been described very clearly and can be used by any instructor who would like to use for his or her purpose qualitative indicators of confusion and confidence.

Reference:

1. “Making sense of confusion: Relating performance, confidence, and self-efficacy to expressions of confusion in an introductory physics class”, Jason E. Dowd, Ives Araujo, and Eric Mazur, Phys. Rev. ST Phys. Educ. Res. 11, 010107 – Published 3 March 2015, http://journals.aps.org/prstper/abstract/10.1103/PhysRevSTPER.11.010107

2. Hake, R. 2002. “Lessons from the physics education reform effort.” Conservation Ecology 5(2): 28. [online] URL: http://www.consecol.org/vol5/iss2/art28/

3. “Teachology 99.9: Everything, people who care about education, should know about teaching”, Valentin Voroshilov, http://teachology.xyz/Teachology99.htm

4. “Critical reading of “Making sense of confusion” by Jason E. Dowd, Ives Araujo, and Eric Mazur”, Valentin Voroshilov http://www.scipublish.com/journals/EPI/papers/1404 ; or https://www.academia.edu/11527712/Critical_reading_of_Making_sense_of_confusion_by_Eric_Mazur_et_al

P.S. Below I offer the comment on my first draft from the reviewers of the magazine. The first one is fairly technical. But the second one made me feel very at ease, because the reviewer expressed many sentiments similar to my own views (FYI: thanks to the reviewers, the final version of the paper has significant changes from the first draft).

_________________________________

• EXPERT 1

• Technical Points: 2

• Original Creativity: 3

• Words & Grammar: 2

• Relevant to Journal: 4

• Topic Novelty: 4

The article is interesting but needs to have some heavy editing. For example, it uses abbreviations (such as Phys. Rev. special topics – PER.) in the text and in the title (such as Mazur et al.) and goes into different directions.  There is a lack of focus from one section to the other. Perhaps the authors can develop and outline so that the manuscript follows this outline.

Also an organizer needs to be included at the beginning of the manuscript. This will help both the authors and readers to understand the manuscript. 

Subheadings would also be helpful in making transitions rather than having new ideas jump at the reader all of a sudden.  it is highly recommended that the authors have a professional editor work on the manuscript

• EXPERT 2

• Technical Points: 5

• Original Creativity: 5

• Words & Grammar: 5

• Relevant to Journal: 5

• Topic Novelty: 5

This is a real educational research paper. I strongly recommend its publication. I hope this journal can become a forum to attract more papers like this one.

(1) I quite agree with the author that most papers published in voice-leading science education journals are in fact a part of an academic game, which only result in negative effects on education. It is not exaggerated to say that every paper one comes across in such journals is rubbish. Even the policies of teaching content orientated journals are not quite right. There should be a forum to correct this problem and the task cannot be accomplished by the voice-leading science education journals, at least not in their current forms.

Most of the science educational papers sound scientific by using statistical methods but in fact they are nonsense. Most science educational specialists do not even understand the very basic fact that science education is in essence science teaching.

They only contented with the superficial understanding of science. The chemical educational specialists are not chemists at all; the physics educational specialists may not be real physics teachers; the mathematical educational specialists may not be mathematicians. All the science education specialists are educational specialists but they even might not be qualified to be science teachers.  (2) By the way the sentence

“(b)The fact that different students may have different thoughts about themselves (in the variety of contexts) is also a part of an every day experience of an every teacher (and again, we will not discuss in this paper what is the best strategy for a teacher teaching a class with students who have different self perceptions).”

Should be read as: (b)The fact that different students may have different thoughts about themselves (in the variety of contexts) is also an everyday experience of every teacher (and again, we will not discuss in this paper what the best strategy is for a teacher teaching a class with students who have different self-perceptions).

(3) In the following sentence, “per-to-peer” should be peer-to-peer. “An interesting research question is what type of work (step by step guiding, giving away an answer, initiating per-to-peer conversation, etc.) and under what circumstances would be the most efficient why to decrease or “eliminate” that particular confusion.”

_________________________________

The End

Dear Reader, thank you for staying with me.

Please, feel free to critique.

I hope for hearing from you your thoughts and suggestions.

-----------------------------------------------------------------

Dr. Valentin Voroshilov
teachology.xyz

P.S. Some good books to read for a person at the beginning of a teaching career:

1. How people learn // ISBN 0-309-07036-8

3. How to solve it, by G. Polya // ISBN·13, 978·0·691·11966·3

4. Toward Science of Education, by James M. Kauffman // ISBN: 978+57B617-68-5

5. Learning, Creating, and Using Knowledge, by Joseph D. Novak // ISBN 9781135184469

6. Future wise, by David N. Perkins // ISBN: 978-1-118-84408-3

7. Educational Research, by Edward L. Vockell, and J. William Asher // ISBN-13: 978-0024231055

8. The Teacher Wars: A History of America’s Most Embattled Profession, by Dana Goldstein // ISBN: 978-0-385-53695-0

9. Becoming a secondary science teqcher, by Jazlin V. Ebenezer and Sharon M. Haggerty // ISBN: 0-02-331312-9

10. The Open Society and Its Enemies, by Karl Popper // ISBN: 978-0-691-15813-6

I am Dr. Valentin Voroshilov.

I have been teaching physics and mathematics to all possible categories of students, including middle school students, high school and college students, teachers, and students with learning difficulties. I have been consulting school and district administrations on how to increase efficiency of teacher professional development (more at teachology.xyz). I also have published various papers describing my views (including some unorthodox ones) on the theory and practice of education. This book is based on my experience and my publications and offers to a reader a number of insights on how to address, analyze, and fix some of the many issues currently experienced in education in general and in STEM education in particular. Some of my views might seem way off the mainstream opinions and contradicting commonly accepted concepts. That is why I invite readers to an open discussion.