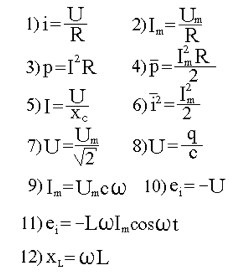Teaching Philosophy

I believe, a contemporary physics course has to be built up on the principles of constructivism and has to employ inquiry-based strategies of teaching; the most fundamental pedagogical concept which has to be placed in a center of all teaching techniques is Zone of Proximal Development (see below).

In a standard undergraduate course an instructor provides students with basic concepts and ideas, which have been developed in the field. Students should get some hand on experience in the labs, and discussions should provide students with examples of how to apply basic concepts and ideas for solving certain problems. The main difficulty with this approach is that students very quickly have to develop on their own many specific problem solving methods which have been developed in the field for a number of decades or even centuries.

When study a physics course based on inquiry-based strategies of teaching, students should develop the fundamental concepts and ideas while working through combined discussion/lab activities (investigative laboratories). The lecturer should guide the students through problem solving techniques and procedures to help them to learn how to apply the fundamental concepts to solving specific physics problems. Nowadays a textbook is not very important any more, since there are so many reachable sources students can use for free, for example, online resource like http://www.wikipedia.org/; rwc.uc.edu/koehler/success.html; http://hyperphysics.phy-astr.gsu.edu/hbase/hframe.html; etsu.edu/physics/lutter/courses/phys2020/index.htm; physics.bu.edu/demos (T, V); physics.bu.edu/ulab, and similar.

A problem-solving oriented approach to teaching physics solves the accountability issue and offers a universal and fair way to assess students’ level of conceptual understanding and of mastering problem solving skills. It is my belief that if a student can solve any problem similar to 500 (or more) standard physics problems, that student deserves an A for the course. All we need to do is to agree on the list of those problems.

Of course, there is also a question of what should a teacher do to help students learn how to solve problems? The answer to this question depends upon the experience of the person who answers it (below I give short description on my professional experience). In general, my answer to this question is that in order for helping students learn how to solve problems a teacher should NOT teach them how to solve particular physics problems but should teach how an expert problem solver comes up with the solution of a problem which he or she sees the first time in his/her life. The mystery which a teacher should be uncovering is how an expert who solves problems has been constructing the solutions to them, how he or she has found that the problem has to be solved in exactly that way it was solved?

How to learn physics

I have heard many times (as thousands of other physics teachers) a student saying that he or she knows physics but does not understand some of the concepts and cannot solve problems.

I always say in return, that there is not much in physics what needs some kind of extraordinary understanding; physics is one of the most clear (and I would add easy) subjects, since it has a very straightforward logic. However in order to teach how to solve physics problems a teacher should not be focusing on demonstrating how to solve specific physics problems (!), but instead should demonstrate the thinking process happening when an expert problem solver is constructing a solution for a given problem. So, when a student does not know how to solve a problem, he or she should ask a question “how to solve this problem?” and then ask a question “how did you come up with this solution?” And a teacher should be demonstrating the solution, as well as demonstrating the thinking process of the creating of that solution.

Here are some inputs on the fundamentals for the thinking process in problem solving in physics.

Not everything in physics requires understanding. There are some important physical concepts, which do not require understanding, but require memorizing; in a standard physics textbook all those concepts are laid out in paragraphs “facts to learn” (or similar). Well, of course, some understanding is required, for example, understanding of the meaning of the words and sentences (that is why I do not write in Russian the book aiming at American students). The set of the memorized facts comprises that knowledge, which someone might mean when saying “I know physics”.

The next level of understanding comes when students are making connections between the just learned concepts (which might be of an abstract kind) and their knowledge of everyday life around them. The existence of these connections makes students say “I understand physics”.

But the true (actual, complete) understanding underlines the ability to apply previously accumulated knowledge for analyzing specific physical situations and comes with the experience of solving specific physical problems, as well as tests by the ability to solve physics problems.

The best (and only!) way for achieving this kind of understanding is solving physical problems (it is like learning how to drive a car, or how to swim; no one can do it just by watching how other people do that; it requires a lot of personal practice, preferably under guiding by an experienced instructor).

If you read a text of a problem and you know what to do, it is not really a problem; it is rather just a training exercise. A real problem happens when you do not know what to do and have to construct the solution on a spot.

In order to solve this kind of a problem, you (and everyone else on the Earth) have to:

1. wish to solve the problem (otherwise you will find many excuses for not doing that);

2. start acting, start doing something problem related, start solving the problem;

3. keep trying until you finally get it solved, if one attempt does not work, try something different, generally there are only two reasons for not having yet a problem solved, which are either you made a mistake in one of your steps, or you are missing some important information, so look back at all your steps and at all facts or rules you have been using, ask yourself what might be missing or could go wrong, and try again.

There are also some specific hints useful when solving a physics problem:

1. decompose the problem into elementary parts - clarify the problem, analyze the meaning of each word, ask a question to each word or sentence – what does it mean? In physics nouns usually mean specific objects, verbs mean some processes happening to the objects, adjectives characterize properties of the objects, adverbs characterize properties of the processes;

2. use a visual aid to express all the important objects, processes and their features involved in the situation, for example, draw a picture or a variables connections web (see below) or both;

3. try to describe the situation in more general (abstract) terms (use your knowledge of physics), make a translation of the text of a problem from the everyday language to the scientific language (see below an example of a dictionary);

4. classify the physical situation describe in the problem (see below an example of a classification), do you recognize the situation?

5. write down the mathematical expressions which you think may be useful for the situation you are analyzing (make a guess, venture an idea);

6. solve the math;

7. reflect on the results, do the make sense for you?

Some helpful questions you can ask to yourself when solving physics problems:

1. What objects are involved?

2. What properties of the objects might be important?

3. How can I reflect all the important objects, process and their properties in a picture?

4. What do I know about this kind of objects and this kind of process? Have I solved a similar problem before?

5. How to describe properties of the objects and processes mathematically (by numbers or equations)?

6. What is happening to the objects? (Make a picture showing the objects and the processes they are involved into).

7. What properties of the processes might be important? How can we describe them mathematically (what laws or definitions should we use)?

8. Are all the variables connected? What else should be connected to what?

9. How can I solve my equations mathematically (a guess!)?

10. Does it make a sense?

11. Could I solve a similar problem again? How much time would it take?

12. Who can help me (if I need it)?

Of course, if you know what to do you do not have to make all the steps and ask all the questions from above; but if you do not know what to do any of those steps and questions might become a turning point in creating your solution!

As I often like to say, study physics without solving problems is the same as learning how to swim with ever entering in water. To learn how to swim is necessary to swim, i.e. to lie down on water, start moving hands and legs, and see what happen. At the very first time, certainly, you will fail; you will drink some water and move to nothing, but gradually, from a try after a try you will be doing better and better. And the time will come when the first swim is accomplished! You can swim now!

Precisely same situation occurs with a solution of physics problems (and, actually, with any other everyday problems). To learn how to solve problems is necessary to solve problems: to read a text and conditions, to imagine as clearer as possible a circumscribed situation, to draw a sketch, to write down formulas and to try to make sense of them. And of course, at some point in construction your solution you will make a mistake. Making mistakes is a natural thing when solving problems. However, making mistakes is a necessary thing when learning how to solve problems. Learning actually gets triggered only when a mistake had been made and a student starts thinking about how to correct it (People say “learn from your mistakes”, but in reality there is no other way to learn!). “If you didn’t succeed first time, try and try again” rule is partially correct, but every new trial has to differ from the previous ones, because you do not want to make the same mistake again and again. That means, when you make a mistake you should figure out what went wrong (or at least make a guess on that).

The very first difficulty many students run into when they have to solve a problem is “how to begin”? My usual answer is “try something, anything”.

Let's assume, that you are invited to a party. You come, and there are so many unfamiliar people over there. What do you usually do in this kind of a situation? You usually are trying to find somebody familiar and approach him or her.

The exactly same thing is happening when we start solving a problem. Our brain is a powerful patter-recognition computer, and the first thing it does in a problematic situation is starting looking for familiar patterns. And it finds them, even if we do not feel that way. So, if you do not know what to do, your brain knows, so just trust it and do the first thing which comes to mind, but DO IT!

Of course, you can help your brain to find the appropriate pattern faster and with more confidence by using learning aids described above and below (the sequence of steps, a set of questions, a picture, a Variables Connections Web, a dictionary, a model classifications, etc.)

When you are looking for a familiar person, your brain automatically analyzes a set of indicators, like a face expression, a voice, speaking manners, a gait, a shape of a figure, etc. And a physical problem has indicators, too, which, differ one problem form another, but also attract similar problems into a cluster, and when you recognize to which cluster this problem belongs, you can immediately employ from the past the method for solving similar problems.

Physics studies specific phenomena, i.e. specific processes happening to various objects.

Phenomena are the first thing we all observe from our birth. We feel a lot of things, we can see, we can smell, we can touch objects around and hear sounds. And we have developed many words we use to describe these phenomena to each other. But in science we have to use a specific language, which is purified version of an every day language (the main reason is to minimize misunderstanding between scientist). And when we read a text of a problem we often have to make a translation from an everyday language to its scientific version. This is a skill which every expert problem solver has, which can be trained and for which there are also specific learning aids to use, such as a dictionary (see below).

One important thing to remember when solving physics problems is that in physics we NEVER can solve any real world problem, because all real world problems are too complicated! We always must make some simplifications, some assumptions which make the situation described in a problem being manageable. Instead of actual objects we use idealizations, i.e. abstract objects which do not exist in nature but have the same important properties as the real objects in a problem. For example, we do not draw the Earth to scale keeping its exact shape with all the oceans and continents, we just draw a sphere. When solving a problem, it is important to make a clear statement of the assumptions which are made, because (a) our solution is limited by these assumptions, and (b) if something goes wrong, maybe it because one of assumptions was incorrect and we have to rethink them.

Since we do not deal with the actual world, but rather with an imaginary world which, in a way, is a reflection of the actual world, having a good imagination is as useful as being good at math.

Physics studies what happens to the objects around us and why. Some objects are huge, some tiny, some very fast, some not moving at all. We use a specific language to name physical objects, to describe their properties, to name processes happening to the objects and to describe the properties of the processes. Any textbook gives a sufficient description of that language and its application for describing our physical world. Every word in that text has a very specific meaning and everyone must know that meaning exactly; usually we call such special words as physical quantities and use letters (or variables) for a short representation of those quantities in the equations we write. Each equation represents a specific connection between variables.

Physicists, as all scientists, are always looking for patterns. A pattern is a process which repeats itself (as long as we do not change the conditions in some drastic manner). When we find a pattern, we call it “a law”. We use laws to predict what might happen under certain circumstances and to build devises which do what we want them to do. Ideally, a law should be written in a mathematical form (i.e. as an equation), so we could use math to derive our predictions. In physics there are only two fundamental kinds of equations, each equation is ether a definition or a law. A definition is basically an agreement between all the physicists in the world on the meaning of a variable. Definitions come mostly from observations of the objects and processes. A law is a well established mathematical connection between variables (previously defined), and laws come from experiments.

Of course, there are many additional relationships which are derived from laws and definitions by algebraic manipulations, which also might be very useful when solving problems.

As soon as we know all the definitions and laws, we can stimulate our brain for creating a solution of a certain problem, we can reflect on our way of thinking and make a correction (if needed), and we can write and solve all the necessary equations – and when practicing in doing all this - we become experts in solving physics problem.

Let’s give short example of thinning as a physicists. Let’s say we need to find the speed of a metrological satellite which is orbiting the Earth. At first we recognize in this problem the following situation: there are two objects (the Earth and the satellite), they interact with each other via gravitational attraction, the Earth is not moving (our assumption), the satellite makes a circular motion with the Earth at the center of the circle. Key concepts for recognizing the physical situation described in the problem are “gravitational attraction” and “circular motion”. We know, that “attraction” is a kind of interactions and interactions give rise to forces, and forces are related to other properties of objects and their motion via the Newton’s second law. We also know that for an object making a circular motion there are specific relationships between its kinematical variables (for example, speed, acceleration, radius). This information is already enough to start constructing the solution. We can draw a picture, we can write the equations we have mentioned, and start manipulating with the equations until we get a relationship between the speed of the satellite and other important parameters of the problem. If we got it, we are done, if not, we start looking for a missing link or for a mistake in our previous reasoning.

A word to a teacher

Everyone can drive, but not everybody is a good driver; anyone can cook something, but not everyone is a chef. Same is true for teachers. Anybody can tell stories to an audience and express their own experience, but to be a Teacher one needs something more than just that.

A Teacher must have his or her own teaching philosophy as a framework for all decisions a teacher makes in and outside a classroom.

I know this from my one experience of teaching physics and mathematic for more than 15 years, as well as moderating hundreds of workshops for teachers and school officials.

Having received M.S. in theoretical physics and a minor in physics education from one of the top15 Russian Universities I have a solid background in physics and mathematics. I graduated from Perm State University, which is one of the best Universities in Russia. The courses I had taken include Calculus, Analytical Geometry and Higher Algebra, Theoretical Mechanics, Methods of Mathematical Physics, Symmetry Theory, Nonlinear Oscillations, Principles of Tensor Analysis, Differential Equations, Solution of Problems Using Computers, Computing Mathematics, General Physics, Thermodynamics and Statistical Physics, Electrodynamics, Magnetism Theory, Quantum Mechanics, Many Particles Theory, etc.

I have more than 15 years of teaching experience, teaching and tutoring mathematics and physics at all levels of educational system, including middle and high schools, colleges and universities (Perm Technical University, Wentworth Institute of Technology, Boston University, ITT Technical Institute).

I am proud of my ability to explain material clearly and to dissolve a barrier of anxiety many students have when starting study math or physics. I like teaching, and I always do everything I can to helping students mastering the subject.

As a teacher I try to keep in mind that different people learn differently, that passive listening to a teacher is the least efficient learning experience for students, and that the most difference in student achievements comes from the difference in their background.

For a number of years in Russia I used to teach on average 25 lessons a week; my experience includes teaching to almost all categories of students, from fifth graders and to school teachers (that is in addition to an intense tutoring practice and to my full time job at Perm State Technical University and then at Institute for Continuous Education). Teaching and tutoring students of different grades and ages gave me a broad view on internal connections between different skills, knowledge, misconceptions, and a teacher’s impact. Soon I came to a conclusion that “only chosen ones can learn physics and math” is a myth; learning physics and mathematics is not as hard as many people used to think and almost anyone can do that if the teaching strategy is right.

In 1998 I turned to research in education and got my PhD in 2000. I firmly believe in a scientific approach to teaching. A teacher should be able to state specific goals, list the assumptions, formulate criteria of a success, and establish measuring tools and procedures. I have been combining my extensive teaching practice with a considerable experience in developing teaching tools and learning aids for students of different ages. In Russia I was a member of a team developing an automatic testing system to test physics knowledge of prospective students applying at Perm State Technical University. Over the years of my teaching I have developed dozens of dozens of math and physics middle-, and high- school and college curricula, syllabi and lesson plans; problem sets, worksheets and hands-on activities. I have an experience in developing websites and using such ones as webct, webassign, blackboard; creating new demonstrations, filming movies and posting them online, using Java applets and audience responds systems (eInstruction, Turning Technologies); developing other teaching tools useful for onsite and online education.

Based on my teaching and research experience I have finally managed to express my teaching philosophy in a set of short clear statements (which come very useful to explain others my teaching philosophy or to analyze teaching stile of others):

If a person can learn the multiplication table he or she can learn quantum gravitation, and there are only two reasons for that not happening - no desire, or a wrong teacher.

Teaching is guiding students through an arrangement of learning experiences specifically designed for helping mastering the subject.

Teaching = motivating + demonstrating + instructing + explaining

Learning = goal making + memorizing + reiterating + thinking

Understanding = making sense of the things by connecting the previous knowledge with the current experience.

An expert problem solver = solid life experience + problem solving skills + mathematical abilities.

A good teacher is not the one who loves teaching, but the one who loves learning and is passionate in sharing this love.

If you are a good teacher, your students understand your solutions to problems; if you are a great teacher, your students create their own solutions.

Learning does not happen by watching, it happens by doing.

You can watch for ours other people swimming, but if you want to learn how to swim you have to get yourself into water and start trying.

Reading (and watching, and listening) helps to form an initial vocabulary, and to set relationships between the current knowledge and the upcoming one. Doing forms the skills.

Practice makes perfect!

If you cannot clearly explain your subject, you do not understand it yourself.

Want to achieve a better understanding? Try to explain it to someone!

The “learning space” of students in a class is (essentially) three dimensional: they might differ by their 1. background (previously learned knowledge and skills); 2. learnability (rate and volume of attaining knowledge and skills as a function of time and effort); 3. motivation (aspiration and willingness to learn).

The best gift a parent can give to a child is good habits; the best gift a teacher can give to a student is love for learning.

Look at infants – they always try things and want to learn something new! Now look at school graduates – so many of them do not want to learn anything new. Do we really need schools like that?

Kids do not know anything and learn everything from scratch. When adults learn new skills they repeat the same general steps and stages of learning they used to use when where kids (but usually faster).

Teachers - like doctors – have to take “ a Hippocratic Oath of a Teacher” or at least to promise “never do harm to anyone”, because there is always something more important in teaching than merely transmitting knowledge.

If you are a teacher you need your own teaching philosophy as a measure stick against which you assess your teaching performance. “Your own” does not mean “unique”, it means that you firmly believe in it (until facts of your life do not make you rethink it).

Developing any philosophy is not an easy thing to do, including a teaching one. Unfortunately many people have a very simplistic view of such a complicated thing as educational psychology and at the same time an overcomplicated view of such a thing as how people learn (in general). As an example of this kind of mixture of views I would like to offer a quick review of the interview given by Mss. Melinda Gates to Mr. Colbert (the Colbert Report, September 27, 2011).

Mss. Gates: “One of the things we’ve learned (during the years of research) is having an affective teacher at the front of a classroom is the singe the most important thing that we can do in the public school system”.

My comment: I firmly believe that it does not make any sense spending so much money (“5 000 000 000 over next few years”) on researching questions, which could be answered by applying a simple common sense. In science there are always some fundamental facts (we call them ‘laws”); as soon as these laws have been established many secondary facts can be derived from them just by using logic. The statement “an effective teacher is the most important part of a learning process” can be derived from a current understanding of teaching (teaching is guiding students through an arrangement of learning experiences specifically designed for helping mastering the subject), which is, of course, is based on the contemporary understanding of how people learn. Imagine a school with NO teachers (human or robotic), and ask what would kids learn over a year in this school, the answer of course is “nothing”, so, why spending millions on proving this simple fact?

The problem is that in education there are too many groups of scientists and officials trying (for many different reasons) to distinguish themselves from others so they resist to come to a commonly used set of laws governing learning and teaching process; many times they invent their own categories to describe the same things, and then wish to conduct a research to support their description of the same ideas (again, and again, and again). Of course, it is just a sign of the fact that the science of education is in its infancy, like mathematics, or physics, or chemistry 3 – 4 hundred years ago. If anyone would want to make sure that money are efficiently spent, he or she should have formed a group of scientist, and ask them to put together a basic dictionary and a set of fundamental rules (facts, laws) which a good teacher should know, and do not give money to anyone who would either not sign up for this “bible on public education”, or who would offer a clear logical argument (in the form of a another set of rules) why he or she would not sign for it up. We have to understand that it is just impossible to express the whole teaching philosophy (some say, teaching is an applied philosophy) in a set of short laws, but having that kind of a set (as a first correction to his or her teaching philosophy a teacher will develop in full in the future) is better than having none, or having too many.

Mss. Gates: “3 000 teacher are being videotaped. The research is not finished yet, but some of the things we’ve learned, that they manage the classroom really well, they get the kids to think very critically, and if a kid does not understand the homework, they get back and re-explain it until the kid gets it”.

My comment: This is another example of the case when a simple logic could lead to the same results. Managing a class is an obvious part of a good teaching (the proof: take a teacher out of a classroom and let students do whatever they want and see what happens); critical thinking is an important part of an effective learning (some say, it is not thinking if it is not critical). Understanding is making sense of the things by connecting the previous knowledge with the current experience. If a student could not do the homework, he or she is missing important connections and if theses missing connections are not fixed, the future teaching will not lead to the completed learning. This is an example of the use of a common sense in education.

Everybody can drive, but not everyone is a good driver, everybody can cook, but not everyone is a chef, why do people think that anybody can be a good teacher? Even if we list all the important qualities, abilities, skills, competencies, etc. of a good teacher, it does not mean anyone can become the one. We have to accept the fact that there is and always will be a distribution of teachers with regard to teaching skills. It might be even more important to understand how to gauge a prospective teacher with a high potential, because that kind of a person will become a good teacher even without anybody’s help (however, the help might speed the process up). From my experience of years of evaluating teachers and helping them to reach the professional level they want to reach, a good teacher is not the one who loves teaching, but the one who loves learning and is passionate in sharing this love.

Mss. Gates: “Over 40 states has signed up to do is to have standards”.

There is a long history of developing standards (not just in the USA), but – evidently - having standards has not been really helpful for improving education. The main reason is that even with a set of commonly accepted standards measuring devices and techniques remain being voluntary (the subject of a subjective choice) and there are way too many of them. As a consequence, there is no way to compare the results of teaching across the country (and, coincidently, to see how well a school or district or state government is doing). The situation with assessment of learning outcomes is such as if every state, or even school district would have being used its own temperature scale whit no conversion factors, and would change it every year. Having a set of clear standards should be the step to developing a (more or less) unified set of measuring devices to assess learning outcomes. There are scholars who say, that is impossible. I would dream of a gathering of scholars who think differently and who would develop such a set, at least as one of the possible (to prove the concept), at least for STEM courses (there is an experience proving the possibility of achieving this goal). Having developed such a set of measuring tools would allow everyone who sign up for the usage of the set to make the effectiveness of teaching transparent and comparable; having such a set of measuring tools is NOT an equivalent of teaching to a test, even if it sounds like that. Developing sophisticated and uniformly accepted measuring techniques and devices helped physics (for example) to grow over its infancy and to become a modern science, and the same should happen to educational research.

The “Bill and Melinda Gates Foundation” issues hundreds of millions of dollars to people who spending the money for developing an understanding of how people learn and what is a good teaching despite the fact that the fundamental ideas underlining any good teaching work has been established decades ago (it would be much smarter investing the money into changing current educational policies).

People learn by an example and by doing things and by overcoming their mistakes.

A god teacher knows his or her subject, can manage the class, he or she is a good listener and a good communicator and entrepreneur. And also has a developed teaching philosophy.

Although, having a developed teaching philosophy does not guarantee that all students will love the teacher. On the contrary, there always will be student disappointed with the teacher despite his or her best effort. This fact is just another law of pedagogy and is a simple consequence of another fact, that all people have different taste in everything, including food, movies, or other people. But there is also another law of pedagogy saying that all students respect a good teacher, because even those guys who do not really like him or her still see and appreciate the effort the teacher makes in his or her teaching and devotion the teacher has to teaching.

A good teacher always tries to do the best possible work, which means he or she is constantly looking for the ways to improve the teaching practices; a good teacher always gets better. A good teacher regularly thinks “OK, in this case I did what I could, what should I learn to do a better job next time?” That means a good teacher is a creative teacher, he/she always thinks of new ways to help students learn. Creativeness is an important feature of a good teacher. As well as an ability to look back, to reflect on what has been done, why it has been done the way it has, what worked as planned and what didn’t, and the ability to plan the future actions on the basis of the reflective analysis. Of course, as a role model, a good teacher always learns, too, he/she learns new subtopics of the subject, new teaching techniques, new learning aids, etc. If one wants to assess the quality of a teacher, one can ask what new the teacher had learned over the last year of teaching.

A good teacher knows the students. There are so many parameters to classify students in a classroom, such as their social background, the background in the subject, the background in the relative subjects (like math for learning physics), the highest concentration level, the ability to work independently of a teacher, the temper, the reason for coming in the school, mental development (memory, attention span, logic), psychological development (especially self-control), etc. It is impossible to accommodate all the student accordingly their full profile, but knowing students’ profiles at least gives an opportunity to do the best a teacher can when tuning the teaching strategies to the class as a whole. Students can feel when a teacher tries his or her best and pay back by the respect and appreciation.

It is very important to be open and honest to students, and to himself/herself. “Why do I teach? Why do I want to teach? Do I want to teach? What is the mission and ultimate goal of my teaching? What does teaching mean to me? What does teaching mean to my students?” These are questions which are fundamentally important for development of the own teaching philosophy, answering questions like that helps to clarify the values a teacher sees in his or her job.

If bringing the highest knowledge possible is the goal of teaching, does it mean using electric shock is an appropriate tool to keep students in line? What is more important, the volume of memorized facts or deepness of kids’ personality?

I believe, the most important rule in teaching is “do no do to kids any harm” which limits all teaching actions. As long as the rule stands, everything else is appropriate. In order to measure the own teaching practice against the ideals a teacher has to have those ideals (i.e. philosophy) but also has to have a developed ability to reflect on his/her own practice.

On Zone of Proximal Development

(By Victor Zaretcki; translation from Russian by Valentin Voroshilov)

Seven statements we lay down below represent in a concentrated manner the Vygotski’s idea of a zone of proximal development and can be seen as a basis for constructing pedagogical (teaching and diagnostic) procedures aimed at development of a child while teaching.

Reconstruction of the Vygotski’s view and projecting it onto the pedagogical application of a zone of proximal development principle leads to the following statements:

1. The first assignment (problem) which a child cannot solve on his/her own represents the boundary between a zone of actual development and a zone of proximal development. It does not make a difference if this is happening under natural circumstances or during the artificial procedure to diagnose the level of child development.

2. When a child cannot solve a problem he/she is in a problematic situation (the goal of a teacher is creating a sequence of problematic situations and guiding students through them).

3. When in a problematic situation a child solves a problem by communicating with an adult (expert).

4. From this point of view child development is a process during which a child undergoes a transition from a mutual work with an adult solving together difficult problems to being able to solve problems independently from adults. The fact this transition happens is also a measure of how effective the help of the adult was: if today a child can alone solve problems which he/she could solve before only with a help from adult, that means the help was effective. If the transition did not happen, that means the adult should think again about the teaching methods he/she uses.

5. It is clear that the region of the zone within which development is growing has another boundary; beyond that boundary lay the problems which a child cannot solve even with the help from an adult. We see that the zone of proximal development is a region having to limits: an upper limit beyond which lay problems too difficult for a child even with a helping adult; and a lower limit beyond which lay problems the child can do without an adult.

6. A zone of proximal development represents an assembly of specific actions; a child can understand what they mean and how they work but cannot implement without help; i.e. this is a zone within which a child acts meaningfully but with a help of an adult. If a child cannot understand an adult and cannot act in a meaningful manner there is no communication and there is no real mutual work of a child and an adult.

7. Finally, we should mention that Vygotski himself though of the zone of proximal development as applicable beyond just intellectual skills of a person.

The next area of discussion can be related to two questions:

1. What kind of a help can and should be used by an adult helping a child in a problematic situation.

2. A look at contemporary teaching methods and techniques from the Vygotski’s point of view on a zone of proximal development.

An example of a dictionary for problem solving

Let’s take the following problem.

1. For a takeoff a plain needs to reach speed of 100 m/s. The engines provide acceleration of 8.33 m/s². Find the time it takes for the plain to reach the speed.

When a physicist read this problem he/she translates it immediately (and intuitively) into the following text:

A body moves from rest with a constant acceleration (which is given) and at some instant of time (which is unknown) has a specific speed (which is given).

Without making this kind of a translation we cannot solve a problem.

A helpful tool to conduct this kind of translation is a dictionary.

For example:

Empirical term (everyday word)	A theoretical term, category	Physical quantities describing the category (and the common notations)
A car, a stone, an arrow, …	A body, An object	A mass (m), coordinates (x, y, z), a volume (V), etc.
Goes, drops, rolls, flies, pulled, pushed, …	Moving, At a motion	Displacement (S), distance (L), velocity (v), acceleration (a), time taken for the motion (t), etc.
Getting at rest, moving from rest, making a turn, …	Changing the velocity, Accelerating	Displacement (S), distance (L), average velocity (v_av), initial velocity (v_i), final/terminal velocity (v_f), , time taken for the motion (t), acceleration (a), etc.
Lies, hangs, sits, …	At rest	The speed is 0, v = 0

An example of a model classification for problem solving

Any process of recognition is always based on some classification parameters and their values.

For example, in high school Kinematics, to identify the model we deal with two main parameters of classification:

1. The form of the trajectory; 2. The behavior of the speed.

Within the standard framework, the following values of the parameters are important:

The form of the trajectory: The behavior of the speed:

a) STRAIHGT LINE; a) DOES NOT VARY (constant);

b) CIRCLE. b) VARIES.

In relation to the values of the parameters, four main kinematics models can be identified.

Form of

Trajectory

Behavior

of Speed

STRAIGHT LINE

CIRCLE

DOES NOT VARY (constant)

Linear motion with constant speed

Uniform circular motion

VARIES

Linear motion with constant acceleration

(Remember, it is not an exact case, but for 99 % of high school problems it is true!)

Circular motion with constant acceleration

(Remember, it is not an exact case, but for 99 % of school problems it is true!)

We cannot use the table to solve any problem on Kinematics, but we can use the principle!

When the model is identified; then we can assemble a set of the most important physical quantities needed to investigate the model, for example as shown in the table below (these are the physical quantities which are most probably involved in solving a problem on Kinematics).

MODEL	MAIN PHYSICAL QUANTITIES
Linear motion with constant speed	Displacement (initial and final points), distance, trajectory, velocity, speed, time taken
Linear motion with constant acceleration	Displacement, distance, trajectory, time taken, initial velocity, final/terminal velocity, (initial and final instant), acceleration.
Uniform circular motion	Displacement, distance, velocity, time, angle, angular displacement, number of revolutions, frequency, angular velocity, period, centripetal acceleration, the radius of the circle.
Uniformly accelerated circular motion	Displacement (initial point, final point), distance, velocity, time, angle, angular displacement, angular velocity, angular acceleration, centripetal acceleration, tangential acceleration, the radius of the circle.
Mixed model	Concepts of parent models; intervals of motion, average velocity, average speed; average acceleration.

Finally, we can write down equations which (most probably) will find the use for solving a problem. For example, the table below represents the correspondence between the models and the formulae which can be used for them.

It is important to emphasize that this step – choosing the equations – is usually the last step of the analysis of the problem (when done by an expert). After this step, merely mathematical calculations are left.

Model	Formulae
Linear motion with constant speed	v = s/t; s = x – x_o, a = 0
Linear motion with constant acceleration	v = v_o + at; s = x – x_os = v_ot + at²/2
Uniform circular motion	; n = N/t; n = 1/T; a_c = v²/R;
Uniformly accelerated circular motion	; ; ; a_c = v²/R; a_t = ε R

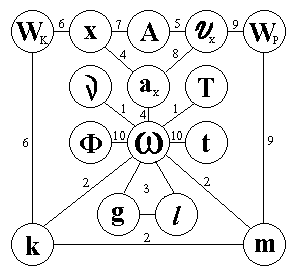
Concept Map

Concept Maps are a powerful instrument to ignite students thinking.

Below there are some examples of a VCW (some had been developed by students during taking physics course).
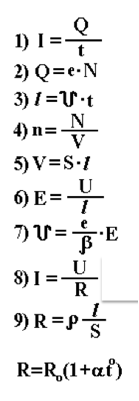
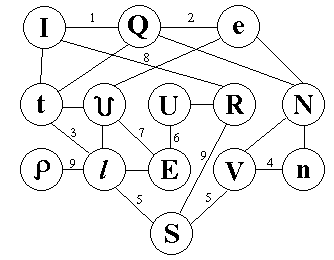
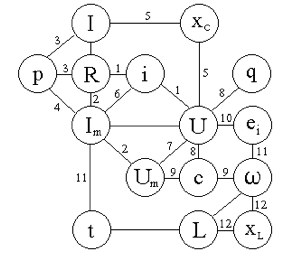
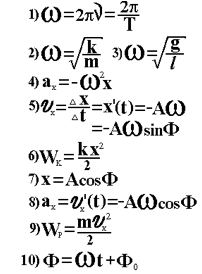