The problem.
An inclined
plain with the length of 1 m and the height of 50 cm has a pulley at its top. A
block of 280 grams, which is on the plain, is connected to a freely hanging 120
grams block by means of a cord passing over the pulley.
Compute the distance the each block
will pass in 2 s starting from rest.
Consider two situations: the
coefficient of kinetic friction is
a) μ = 0.05, b) μ = 0.1
The tips
Types of motion
|
“Check this
out” → ↓ |
trajectory is
a strait line |
trajectory is
no a strait line |
|
speed is
constant |
a
linier motion with a constant velocity (LMCV), acceleration
is 0 (you
can use all the other formulas , which are right for this type of motion) |
usually
it is a circular motion with a constant speed (CMCS), there is a centripetal
acceleration (you
can use all the other formulas , which are right for this type of motion) |
|
speed is no
constant |
usually
a linier motion with a constant acceleration (LMCA) (you
can use all the other formulas , which are right for this type of motion) |
usually
a projectile motion (PM), the acceleration is g = 9.8 m/s2 (you
can use all the other formulas , which are right for this type of motion) |
The second Newton’s law: Fnet = m∙a
The reasoning
As
usual, first, let’s analyze the text
of the problem.
What
objects do we have? What bodies do
we have in this situation? An inclined plain, a block, a pulley, a cord, one
more block. And do not forget about such an important object as Earth. We are
talking about a real situation.
What
kind of characteristics, parameters,
properties can we assign to each of these objects?
The
blocks have a mass. Let’s take a capital letter M for the mass of the first block, and m notates the mass of the second one. Let’s l is the length of the plain, h
is the height.
What
can we say about the cord and the pulley? As usual, we assume that
the cord dose not has any mass, the length of the cord is fixed and there is no
any friction between the cord and the pulley.
After
considering the objects, we go over to physics
processes.
What
kind of processes can we describe in this situation?
We
know already, there are three the most common physics processes: a motion, an interaction and a transformation.
Let’s
talk about motion first.
There
should be a motion in this situation. It is possible the system is in
equilibrium. But, we have some key words
like “the distance” or “pass in 2 s”. These words describe motion. They
mean that the position of the blocks is changing during a time. The changing of the position is motion.
What
type of motion should we consider for this problem? What type of motion do we
have?
Remember,
we have 4 basic types of motion (take
a look on the page I gave you). What type of the motion do we have to use for
our system? We can definitely eliminate the circular motion and the projectile
motion. Now, the bodies start the motion from rest. It means, the speed of the
blocks is changing from 0 to some non-0 number, the speed is no constant. So,
we should eliminate LMCV.
The
only motion we can use is LMCA, a
linier motion with a constant acceleration. Let’s fix it on the board. OK. Now.
What
can we say about interactions? We
have a lot of interactions over here.
Usually,
every interaction produces at least one force.
First,
it is obviously; Earth is acting on
the blocks. The result of this acting is the weight. So, the first block has
the weight, let’s use the capital W for it, and the second block has
the weight w.
Are
there some other interactions? Yes there are. There is an interaction between the block and the cord. It
means, there is a force, which is exerted by the cord and acting on the block.
Let’s use capital T for this force. There is one more interaction between this
block and the cord. We have the force; let mark it with the letter P,
which is acting from the cord on the block.
Do
not forget; any force is a vector, it has a direction.
Talking
about the cord, we have to recall, this is a
special cord, with no mass, with fixed length, without any friction. That
cord has the same magnitude of a tension at any point. It means, the forces T and
P have
the same magnitude. T = P.
In
the end, we have two more bodies, which are interacting. The block and the
plain. This interaction leads to a pair
of forces. The first one is the normal force N, which is keeping the
block on the surface. A normal force works against a weight, it is directing
perpendicularly to the surface.
The
last force is a friction force. This
force is produced by the surface, but its direction is parallel to the surface.
A friction force is a most mystic force among all the named. First, we should
recall that there are two kinds of friction forces; the static friction force
and the kinetic friction force.
Second,
it is not obviously some time how to find the
direction of a friction force. For example, the direction of the kinetic
friction force has to be opposite to the velocity of the body. But, the problem
is; we do not know in what direction the bodies will be moving, when we let
them go. More ever, if the static friction were big enough, there would be no
any motion.
So.
There is a friction force, F.
But, the direction of this force is still an enigma. We cannot begin solving our problem without solving this
enigma. Hence, the first step of the solution is finding the direction of the friction
force.
Any
ideas?
Let’s
say, we do not have any friction at all in the system. Can we find the velocity
of the blocks for the frictionless
system? Yes, we can.
When
we find the velocity of this block with
no friction, the direction of the friction force will be opposite to the
velocity. So, the idea is, we have to solve this problem first without a
friction (we could say that μ = 0). I’m erasing the friction force. And,
the goal is to find the direction of the velocity of this block.
By
the condition of the problem, the block starts the motion from rest. And, as we said already, we have LMCA. By
properties of this type of motion, if the motion is starting from rest, a
velocity and acceleration have the same direction. Hence, we need to find the
acceleration now.
So
what do we have? We have bodies, we have forces and we look for acceleration. Bodies, forces, acceleration. It is
sort of hypnosis.
What
do these key words mean? They mean we have to use Newton’s laws of Motion. Let me recall the most important second Newton’s law of Motion.
The
net force is equal to the mass multiplied by the acceleration.
We
must apply this law to each of the bodies, or at least to one of them.
It
is very convenient using a free-body-diagram.
I want to indicate the plain. And, we have three vectors for the first block: N, W,
T, and two vectors for the second one: P, w.
It
is obviously, the acceleration of the first block should be parallel to the
plain. Let’s assume, that the acceleration is pointing to the top of the plain.
What if we made a mistake, what if the real acceleration goes to the bottom?
We’ll find the answer later.
Now
we can write down the second Newton’s law.
The
net force, which is the sum of all these forces, N + T + W is equal to the mass M
times A.
To
calculate some quantities we have to convert the vectors into some numbers. We need to choose X and Y-axis. The
most convenient way is to direct the X-axis along the acceleration, and the Y-axis
along the normal force. Now we can write the second Newton’s law in components,
which are numbers.
We
have three forces, the acceleration and two components for each of the vectors.
Let’s make the table.
|
vectors\components |
X |
Y |
|
N |
Nx
= 0 |
Ny
= N |
|
T |
Tx
= T |
Ty
= 0 |
|
W |
Wx
= -Wsin(α) |
Wy
= -Wcos(α) |
|
A |
Ax |
Ay
= 0 |
The
X-component of the normal force is 0. The y-component is equal to the length of
the vector, that is, to the magnitude of the force.
The
X-component of the “pulling” force T equals to its magnitude. But, the
Y-component is 0.
The
more zeros, the better.
The
acceleration looks like the force T. But, we are not sure about the
direction of the A, it can be opposite. So, we can write just Ax
and 0.
I
want to recall, we are looking for the acceleration. Hence, we want to find
this number. It is possible to get the negative number for Ax. If so, what
would be that mean? The negative number
for Ax means,
the real acceleration is directed in opposite direction, that is, to the bottom
of the plain.
OK,
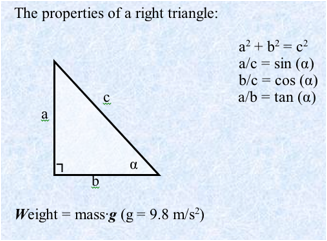
we have one more force to break it down into components. The weight.
Unfortunately,
we have to keep two components of the weight. This is the X-component, and that
is the Y-component. W, Wx
and Wy form the right triangle, which I want to draw separately. We have two
legs and the hypotenuse. The lengths of the legs are equal to the magnitude of
the components. By properties of a right triangle, we can write the following
formulae. We can solve these equations for the components. Because, the
components are directed against the axis, they have to be negative. It means Wx
= -Wsin(α) and Wy = -Wcos(α).
Now
we can write down the second Newton’s law in components.
First,
we have to rid off the small arrows over
the vectors, and write down instead of them small letters x and y, which
indicate the components.
Instead of one vectorial equation we have now two scalar
equations.
Nx
+ Tx + Wx
= M*Ax
and Ny
+ Ty + Wy
= M*Ay .
The second step is; we have to substitute the values of the
components, taking them from the table and plugging into the equations.
It
leads to following equations. 0 + T -
Wsin(α) = M*Ax
and N + 0 - Wcos(α) = M*0 After taking in account all zeros, we
got
T
- Wsin(α) = M*Ax and N
- Wcos(α) = 0
If
you have any questions, you have to
stop me at any time and ask your question.
OK,
I have a question, who remember yet
what are we looking for?
We
want to find the acceleration (which is necessary to find the velocity, which
is necessary to find the direction of the friction force).
May
be we can find Ax already? How can we check
it out? We can just plug all the numbers into the equation. This is the
first time during the solution, when we have thoughts about numbers. It is because
Physics is more than just Algebra or Geometry. Physics is a special way of
thinking about Nature.
OK.
Let’s go to the numbers.
What
must we have done before using any numbers? We have to convert all the numbers
into the International System of
units. So, we have the mass of the first block is 280 grams, which is exactly
.28 kg.
…
What
numbers can we use right now to compute the acceleration? We do not have T, no
W, no alfa. We can plug into the equation just 0.28.
Ax
is unknown. It’s obviously; we need more
numbers, that means, we need more information. Let’s start with alfa. Alfa is a geometrical quantity. We have
two more geometrical quantities; l and h. Probably there is a connection
between all this geometrical stuff. We need a good sketch. The plain, the
length is 1 m. The height is .5 m. this is a right angle, So, we have a right
triangle. The hypotenuse is 1, the leg is .5. We can find any angles for this
triangle. The question is; what angle do we need to find? What of these two angles is equal to alfa?
Let’s
see. This is a right angle, which is 90 degrees. Hence, this angle is 90
– alfa. I can make one more right triangle. This angle is 90 – (90
– alfa) which = alfa.
By
the property of a right triangle, while the leg is opposite to the angle, the
leg divided by the hypotenuse equals sin(alfa).
Plug
the numbers. We’ve got sin(alfa) = .5, that means alfa = 30 degrees.
OK.
We have found one more number for this equation. Next letter is W. W indicates the weight of this block.
Weight is a special word; there is a definition for a weight. A weight equals
mass multiplied by the acceleration due to the gravity. We know the mass, and
we know g. Hence, we can calculate the weight.
W
= .28*9.8 = 2.744 N.
After
all the numerical considerations, we have now the equation:
T
– 2.744*sin(30) = .28*Ax
We
cannot solve this equation to find Ax,
because we do not know T.
The
second equation is not helping, because it dose not content T.
We
still have a deficit of information. We need some additional source of information.
What could it be?
We
have the second body. We can apply the second Newton’s law to this body. It
should be helpful. At least, we do not have any more resources.
There
are just two forces, which are acting on the small block. The second Newton’s
law for the block has to be written as following: P + w = m a
The
direction of the acceleration a cannot be chosen at our will.
There is a connection between the
motions of the blocks. When that block goes to the top of the plain, this
block goes downward. Why? Because of the gravity and because of the cord.
We
have to direct the acceleration downward. Let’s choose the X-axis downward as
well. These to vectors have the positive components, but that have the negative
one. We can write –P + w = m*ax
We
know the mass m = .12 kg, and we can find easily the weight w = .12*9.8 = 1.176
N. What can we say about P? We already have talked it of. P = T. The magnitudes
of these forces are equal. Therefore, we can write T instead of P.
The last letter,
which we have to talk of is ax. ax is the acceleration of
the second block. This block is connected by the cord to that one. And, the
length of the cord is fixed. It means, that when the first block pass any
distance, the second one must pass exactly the same distance in exactly the
same time. Therefore, the magnitudes of the velocities and the accelerations of
the blocks are the same.
Ax
= ax.
(By
the way, can I write A = a?)
Let’s
make our last substitution, let’s write Ax instead of ax.
After
all these manipulations, we have two the following equations
T
– 2.744*0.5 = .28 * Ax
-T
+ 1.176 = .12*Ax
We
do not need to know T. Let’s eliminate it simply by addition of the equations.
T
– T = 0. -2.744*.5 + 1.176 = -.196
.28 + .12 = .4 In the end of all computations we have A x = -.196/.4 =
-.49 m/s2
It
dose not matter what number did we get. The point is this number is negative.
It means, the acceleration of the first block is directing
to the bottom of the plain. So do the velocity. And, at last, we can say with
sure that the direction of the friction force is opposite to the velocity, that
is, the friction force is directing to the pulley. Finally, we’ve got it. I want to draw the
friction force on the picture, and on the free-body-diagram. Now, we can start solving the original
problem.
But
it will be your home work.